Main Content

线性预测设计

打开实时脚本

此示例说明如何设计线性神经元来预测给定最后五个值的时间序列中的下一个值。

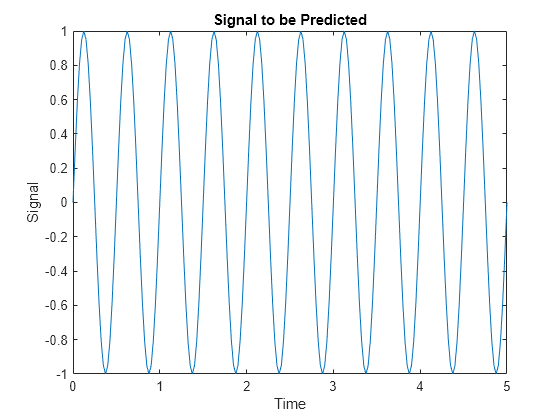
定义波形

此处，时间定义为 0 到 5 秒，步长为 1/40 秒。

time = 0:0.025:5;

我们可以定义关于时间的信号。

signal = sin(time*4*pi);
plot(time,signal)
xlabel('Time');
ylabel('Signal');
title('Signal to be Predicted');

为神经网络设置问题

然后将信号转换为元胞数组。神经网络将时间步表示为一个元胞数组的各列，并将它们与在给定时间的不同样本区分开来，后者用矩阵列表示。

signal = con2seq(signal);

为了设置此问题，我们将使用信号的前四个值作为初始输入延迟状态，其余的值（最后一个时间步除外）作为输入。

Xi = signal(1:4);
X = signal(5:(end-1));
timex = time(5:(end-1));

目标现在定义为匹配输入，但前移一个时间步。

T = signal(6:end);

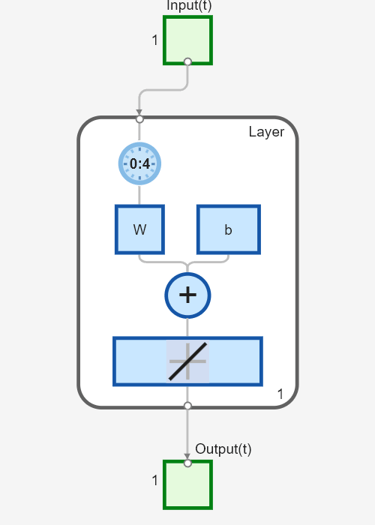
设计线性层

函数 newlind 现在将设计具有单个神经元的线性层，该层在给定当前值和四个过去值的情况下预测信号的下一个时间步。

net = newlind(X,T,Xi);
view(net)

测试线性层

现在，可以对输入和延迟状态调用网络（就像调用函数一样），以获得它的时间响应。

Y = net(X,Xi);

绘制输出信号与目标。

figure
plot(timex,cell2mat(Y),timex,cell2mat(T),'+')
xlabel('Time');
ylabel('Output -  Target +');
title('Output and Target Signals');

还可以绘制误差。

figure
E = cell2mat(T)-cell2mat(Y);
plot(timex,E,'r')
hold off
xlabel('Time');
ylabel('Error');
title('Error Signal');

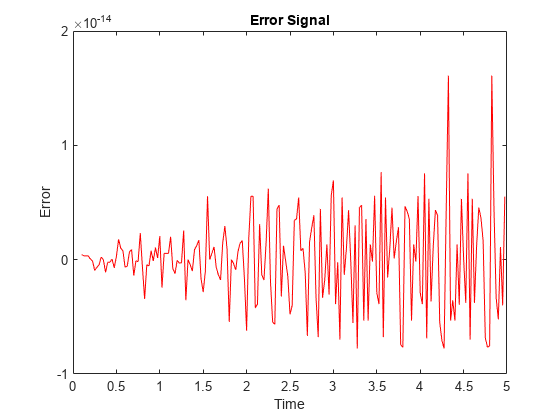
注意误差有多小！

此示例说明如何设计动态线性网络，它可以根据当前值和过去的值预测信号的下一个值。