径向基逼近
此示例使用 NEWRB 函数创建一个径向基网络,该网络可逼近由一组数据点定义的函数。
定义 21 个输入 P 和相关目标 T。
X = -1:.1:1; T = [-.9602 -.5770 -.0729 .3771 .6405 .6600 .4609 ... .1336 -.2013 -.4344 -.5000 -.3930 -.1647 .0988 ... .3072 .3960 .3449 .1816 -.0312 -.2189 -.3201]; plot(X,T,'+'); title('Training Vectors'); xlabel('Input Vector P'); ylabel('Target Vector T');

我们希望找到一个可拟合这 21 个数据点的函数。一种方法是使用径向基网络来实现。径向基网络具有两个层,分别是径向基神经元的隐藏层和线性神经元的输出层。以下是隐含层使用的径向基传递函数。
x = -3:.1:3; a = radbas(x); plot(x,a) title('Radial Basis Transfer Function'); xlabel('Input p'); ylabel('Output a');

隐藏层中每个神经元的权重和偏置定义了径向基函数的位置和宽度。各个线性输出神经元形成了这些径向基函数的加权和。利用每层的正确权重和偏置值,以及足够的隐藏神经元,径向基网络可以以任何所需准确度拟合任何函数。以下是三个径向基函数(蓝色)经过缩放与求和后生成一个函数(品红色)的示例。
a2 = radbas(x-1.5); a3 = radbas(x+2); a4 = a + a2*1 + a3*0.5; plot(x,a,'b-',x,a2,'b--',x,a3,'b--',x,a4,'m-') title('Weighted Sum of Radial Basis Transfer Functions'); xlabel('Input p'); ylabel('Output a');

函数 NEWRB 可快速创建一个逼近由 P 和 T 定义的函数的径向基网络。除了训练集和目标,NEWRB 还使用了两个参量,分别为误差平方和目标与分布常数。
eg = 0.02; % sum-squared error goal sc = 1; % spread constant net = newrb(X,T,eg,sc);
NEWRB, neurons = 0, MSE = 0.176192
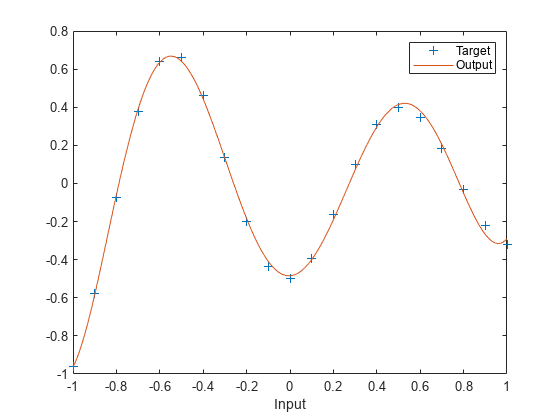
要了解网络性能如何,请重新绘制训练集。然后仿真网络对相同范围内的输入的响应。最后,在同一图上绘制结果。
plot(X,T,'+'); xlabel('Input'); X = -1:.01:1; Y = net(X); hold on; plot(X,Y); hold off; legend({'Target','Output'})