LPC to LSF/LSP Conversion

Convert linear prediction coefficients to line spectral pairs or line spectral frequencies

Libraries:
DSP System Toolbox / Estimation / Linear Prediction

Description

The LPC to LSF/LSP Conversion block converts linear prediction coefficients (LPCs) to line spectral pairs (LSPs) or line spectral frequencies (LSFs). When converting LPCs to LSFs, the block outputs match those of the poly2lsf function.

Ports

Input

expand all

A — Linear prediction coefficients
column vector | unoriented vector | matrix

Specify the input linear prediction coefficients as a column vector, unoriented vector, or a matrix. Each channel of the input must have at least two samples.

The input LPCs for each channel, 1, a₁, a₂, ..., a_m, must be the denominator of the transfer function of a stable all-pole filter with the form given in the first equation of Requirements for Valid Outputs. A length-M+1 input channel yields a length-M output channel.

Data Types: single | double

Output

expand all

LSP — Line spectral pairs
column vector | unoriented vector | matrix

Line spectral pairs, returned as a column vector, unoriented vector, or a matrix.

Data Types: single | double

LSFn — Line spectral frequencies normalized in range (0 0.5)
column vector | unoriented vector | matrix

Line spectral frequencies normalized in range (0 0.5), returned as a column vector, unoriented vector, or a matrix.

Data Types: single | double

LSFr — Line spectral frequencies in range (0 π)
column vector | unoriented vector | matrix

Line spectral frequencies in range (0 π), returned as a column vector, unoriented vector, or a matrix.

Data Types: single | double

Status — Validity status of output
scalar | row vector

Validity status of the output, returned as a scalar or a row vector of Boolean values.

1 indicates that the output of the corresponding channel is valid.
0 indicates that the output of the corresponding channel is invalid.

Dependencies

To enable this port, select the Show output validity status parameter.

Data Types: Boolean

Parameters

expand all

Output — Conversion output
`LSP in range (-1 1)` (default) | `LSF normalized in range (0 0.5)` | `LSF in range (0 pi)`

Specify whether the block converts the input linear prediction polynomial coefficients (LPCs) to line spectral pairs (LSPs) or line spectral frequencies (LSFs). You can set this parameter to one of these options:

LSP in range (-1 1) — The block outputs LSP values in decreasing order, equal to the cosine of the LSF values between 0 and π radians. The block does not output the guaranteed LSP values, −1 and 1.
LSF in radians (0 pi) — The block outputs the LSF values between 0 and π radians in increasing order. The block does not output the guaranteed LSF values, 0 and π.
LSF normalized in range (0 0.5) — The block outputs normalized LSF values in increasing order, computed by dividing the LSF values between 0 and π radians by 2π. The block does not output the guaranteed normalized LSF values, 0 and 0.5.

Root finding coarse grid points — Number of search steps
`64` (default) | positive integer greater than 1

Specify the number of search steps n as a positive integer greater than 1. The block divides the interval (−1, 1) into n subintervals of equal length, and looks for roots (LSP values) in each subinterval. You must pick n large enough or the block output might be invalid as described in Requirements for Valid Outputs. To learn how the block uses this parameter to compute the output, see LSF and LSP Computation Method: Chebyshev Polynomial Method for Root Finding. Also see Adjusting Output Computation Time and Accuracy with Root Finding Parameters.

Tunable: Yes

Root finding bisection refinement — Number of bisections
`4` (default) | nonnegative integer

Specify the number of bisections k as a nonnegative integer. Specify the value k, where each LSP output is within $1 / (n \cdot 2^{k})$ of the actual LSP value, where n is the value of the Root finding coarse grid points parameter. To learn how the block uses this parameter to compute the output, see LSF and LSP Computation Method: Chebyshev Polynomial Method for Root Finding. You can also see Adjusting Output Computation Time and Accuracy with Root Finding Parameters. Tunable (Simulink).

Show output validity status — Show status of output validity
`off` (default) | `on`

Select this parameter to show the validity status of output. When you select this parameter, the block enables the output port Status. The Status port outputs a scalar or a row vector with one Boolean element per channel.

1 indicates that the output of the corresponding channel is valid.
0 indicates that the output of the corresponding channel is invalid.

The LSF and LSP outputs are invalid when the block fails to find all the LSF or LSP values or when the input LPCs are unstable. For details, see Requirements for Valid Outputs.

If current output is invalid, overwrite with previous output — Overwrite invalid outputs with previous output
`off` (default) | `on`

When you select this check box, the block overwrites invalid outputs with the previous output. Selecting this parameter activates other parameters for taking care of initial overwrite values (when the very first output of the block is invalid). For more information, see Parameters for Handling Invalid Inputs and Outputs.

When first output is invalid, overwrite with user-defined values — Overwrite invalid first output with user-defined values
`off` (default) | `on`

When the first input is unstable, you can overwrite the invalid first output with:

The default values by clearing this check box
The values you specify by selecting this check box

The default initial overwrite values are the LSF or LSP representations of an allpass filter. The vector that the block uses to overwrite the invalid first output is stored as an internal state. For more information, see Parameters for Handling Invalid Inputs and Outputs.

Dependencies

To enable this parameter, select the If current output is invalid, overwrite with previous output parameter.

User-defined LSP/LSF values for overwriting invalid first output — User-defined LSP/LSF values
vector (default) | matrix

Specify a vector of LSP/LSF values for overwriting an invalid first output if you selected the When first output is invalid, overwrite with user-defined values parameter. For multichannel inputs, provide a matrix with the same number of channels as the input, or one vector that the block applies to every channel. The vector or matrix of LSP/LSF values you specify must have the same dimension, size, and frame status as the other outputs.

Dependencies

To enable this parameter, select the When first output is invalid, overwrite with user-defined values parameter.

If first input value is not 1 — Action to take if first input value is not 1
`Ignore` (default) | `Normalize` | `Normalize and warn` | `Error`

Specify the action to take if the first coefficient of an input is not 1. Set this parameter to one of the following:

Ignore –– The block treats the first coefficient as a 1.
Normalize –– The block divides the input LPCs by the value of the first coefficient before computing the output.
Normalize and warn ––- The block normalizes the input LPCs and displays a warning message.
Error –– The block stops the simulation and displays an error message at the MATLAB^® command line.

For more information, see Parameters for Handling Invalid Inputs and Outputs.

Block Characteristics

Data Types	`double` \| `single`
Direct Feedthrough	`no`
Multidimensional Signals	`no`
Variable-Size Signals	`no`
Zero-Crossing Detection	`no`

More About

expand all

LSF and LSP Computation Method: Chebyshev Polynomial Method for Root Finding

Note

For more information on the principles on which the LSP and LSF computation methods in the block are based, see References.

To compute LSP outputs for each channel, the block relies on the fact that LSP values are the roots of two particular polynomials related to the input LPC polynomial; the block finds these roots using the Chebyshev polynomial root finding method, described next. To compute LSF outputs, the block computes the arc cosine of the LSPs, outputting values ranging from 0 to π radians.

Root Finding Method

LSPs, which are the roots of two particular polynomials, always lie in the range (-1, 1). (The guaranteed roots at 1 and -1 are factored out.) The block finds the LSPs by looking for a sign change of the two polynomials' values between points in the range (-1, 1). The block searches a maximum of k(n – 1) points, where:

n is the value of the Root finding coarse grid points parameter.
k is the value of the Root finding bisection refinement parameter.

The block's method for choosing which points to check consists of the following two steps:

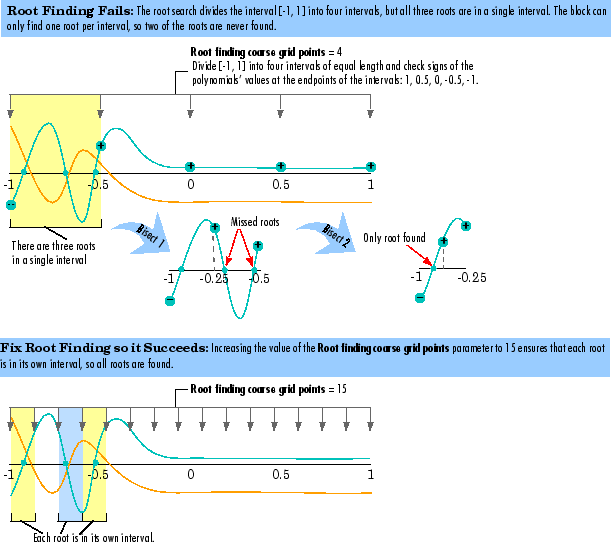
Coarse Root Finding —- The block divides the interval [-1, 1] into n intervals, each of length 2/n, and checks the signs of both polynomials' values at the endpoints of the intervals. The block starts checking signs at 1, and continues checking signs at 1 – 4/n, 1 – 6/n, and so on at steps of length 2/n, outputting any point if it is a root. The block stops searching in these situations:
1. The block finds a sign change of a polynomial's values between two adjacent points. An interval containing a sign change is guaranteed to contain a root, so the block further searches the interval as described in Step 2, Root Finding Refinement.
2. The block finds and outputs all M roots (given a length-M+1 LPC input).
3. The block fails to find all M roots and yields invalid outputs as described in Handling and Recognizing Invalid Inputs and Outputs.
Root Finding Refinement — When the block finds a sign change in an interval, [a, b], it searches for the root guaranteed to lie in the interval by following these steps:
1. Check if Midpoint Is a Root — The block checks the sign of the midpoint of the interval [a, b]. The block outputs the midpoint if it is a root, and continues Step 1, Coarse Root Finding, at the next point, a – 2/n. Otherwise, the block selects the half-interval with endpoints of opposite sign (either [a, (a + b)/2] or [(a + b)/2, b]) and executes Step 2b, Stop or Continue Root Finding Refinement.
2. Stop or Continue Root Finding Refinement — When the block has repeated Step 2a k times (k is the value of the Root finding bisection refinement parameter), the block linearly interpolates the root by using the half-interval's endpoints, outputs the result as an LSP value, and returns to Step 1, Coarse Root Finding. Otherwise, the block repeats Step 2a using the half-interval.

Coarse Root Finding and Root Finding Refinement

Root Finding Method Limitations: Failure to Find Roots

The block root finding method described in the previous section can fail, causing the block to produce invalid outputs (for details on invalid outputs, see Handling and Recognizing Invalid Inputs and Outputs).

In particular, the block can fail to find some roots if the value of the Root finding coarse grid points parameter, n, is too small. If the polynomials oscillate quickly and have roots that are very close together, the root finding might be too coarse to identify roots that are very close to each other, as illustrated in Fixing a Failed Root Finding.

For higher order input LPC polynomials, you must increase the value of the Root finding coarse grid points parameter to ensure that the block finds all the roots and produces valid outputs.

Fixing a Failed Root Finding

Requirements for Valid Outputs

To get valid outputs, your inputs and the Root finding coarse grid points parameter value must meet these requirements:

The input LPCs for each channel, 1, a₁, a₂, ..., a_m, must come from the denominator of the following transfer function, H(z), of a stable all-pole filter (all roots of H(z) must be inside the unit circle). Note that the first term in H(z)'s denominator must be 1. When the input LPCs do not come from a transfer function of the following form, the block outputs are invalid.

$H (z) = \frac{1}{1 + a_{1} z^{- 1} + a_{2} z^{- 2} + ... + a_{m} z^{- m}}$
The Root finding coarse grid points parameter value must be large enough so that the block can find all the LSP or LSF values. (The output LSFs and LSPs are roots of polynomials related to the input LPC polynomial; the block looks for these roots to produce the output. For details, see LSF and LSP Computation Method: Chebyshev Polynomial Method for Root Finding.) When you do not set Root finding coarse grid points to a high enough value relative to the number of LPCs, the block might not find all the LSPs or LSFs and yield invalid outputs as described in Root Finding Method Limitations: Failure to Find Roots.

To learn about recognizing invalid inputs and outputs and parameters for dealing with them, see Handling and Recognizing Invalid Inputs and Outputs.

Setting Outputs to LSFs or LSPs

Set the Output parameter to one of the following settings to determine whether the block outputs LSFs or LSPs:

LSF in radians (0 pi) — Block outputs the LSF values between 0 and π radians in increasing order. The block does not output the guaranteed LSF values, 0 and π.
LSF normalized in range (0 0.5) — Block outputs normalized LSF values in increasing order, computed by dividing the LSF values between 0 and π radians by 2π. The block does not output the guaranteed normalized LSF values, 0 and 0.5.
LSP in range (-1 1) — Block outputs LSP values in decreasing order, equal to the cosine of the LSF values between 0 and π radians. The block does not output the guaranteed LSP values, -1 and 1.

Adjusting Output Computation Time and Accuracy with Root Finding Parameters

The values n and k determine the block's output computation time and accuracy, where:

n is the value of the Root finding coarse grid points parameter (choose this value with care; see the note for more information).
k is the value of the Root finding bisection refinement parameter.
Decreasing the values of n and k decreases the output computation time, but also decreases output accuracy:
- The upper bound of block's computation time is proportional to $k \cdot (n - 1)$ .
- Each LSP output is within $1 / (n \cdot 2^{k})$ of the actual LSP value.
- Each LSF output is within ΔLSF of the actual LSF value, LSF_act, where
  $Δ L S F = | a \cos (L S F_{a c t}) - a \cos (L S F_{a c t} + 1 / (n \cdot 2^{k})) |$

Note

When the value of the Root finding coarse grid points parameter is too small relative to the number of LPCs, the block might output invalid data as described in Requirements for Valid Outputs. You can also see Handling and Recognizing Invalid Inputs and Outputs.

Notable Input and Output Properties

To get valid outputs, your input LPCs and the value of the Root finding coarse grid points parameter must meet the requirements described in Requirements for Valid Outputs.
Length-L+1 input channel yields length-L output channel
Output parameter determines the output type (see Setting Outputs to LSFs or LSPs):
- LSFs — frequencies, w_k, where 0 < w_k < π and w_k < w_{k +
  1}
- Normalized LSFs — w_k / 2π
- LSPs — cos(w_k)

Handling and Recognizing Invalid Inputs and Outputs

The block outputs invalid data when your input LPCs and the value of the Root finding coarse grid points parameter do not meet the requirements described in Requirements for Valid Outputs. The following topics describe what invalid outputs look like, and how to set the block parameters provided for handling invalid inputs and outputs:

What Invalid Outputs Look Like

The channels of an invalid output have the same dimensions, sizes, and frame statues as the channels of a valid output. However, invalid output channels do not contain all the LSP or LSF values. Instead, they contain none or some of the LSP and LSF values and the rest of the output is filled with place holder values (-1, 0.5, or π) depending on the Output parameter setting).

In short, all invalid outputs in a channel end in one of the place holder values (-1, 0.5, or π) as illustrated in the following table. To learn how to use the block's parameters for handling invalid inputs and outputs, see the next section.

Output Parameter Setting	Place Holder	Sample Invalid Outputs
`LSF in radians (0 pi)`	π	$[\begin{array}{l} w_{1} & w_{2} & w_{3} & π & π & π & π & π \end{array}]$
`LSF normalized in range (0 0.5)`	`0.5`	$[\begin{matrix} w_{1} \\ w_{2} \\ 0.5 \end{matrix}]$
`LSP in range (-1 1)`	`-1`	$[\begin{matrix} \cos (w_{13}) \\ \cos (w_{23}) \\ - 1 \\ - 1 \\ - 1 \end{matrix}]$

Parameters for Handling Invalid Inputs and Outputs

You must set how the block handles invalid inputs and outputs by setting these parameters:

Show output validity status (1=valid, 0=invalid) — Set this parameter to activate a second output port that outputs a vector with one Boolean element per channel; 1 when the output of the corresponding channel is valid, and 0 when the output is invalid. The LSF and LSP outputs are invalid when the block fails to find all the LSF or LSP values or when the input LPCs are unstable (for details, see Requirements for Valid Outputs). See the previous section to learn how to recognize invalid outputs.
If current output is invalid, overwrite with previous output — Select this check box to cause the block to overwrite invalid outputs with the previous output. When you set this parameter you also need to consider these parameters.
- When first output is invalid, overwrite with user-defined values — When the first input is unstable, you can overwrite the invalid first output with either:
  - The default values, by clearing this check box
  - Values you specify, by selecting this check box
  The default initial overwrite values are the LSF or LSP representations of an all-pass filter. The vector that is used to overwrite invalid output is stored as an internal state.
- User-defined LSP/LSF values for overwriting invalid first output — Specify a vector of values for overwriting an invalid first output if you selected the When first output is invalid, overwrite with user-defined values parameter. For multichannel inputs, provide a matrix with the same number of channels as the input, or one vector that will be applied to every channel. The vector or matrix of LSP/LSF values you specify must have the same dimension, size, and frame status as the other outputs.
If first input value is not 1 — The block output in any channel is invalid when the first coefficient in an LPC vector is not 1; this parameter determines what the block does when given such inputs:
- Ignore — Proceed with computations as if the first coefficient is 1.
- Normalize — Divide the input LPCs by the value of the first coefficient before computing the output.
- Normalize and warn — In addition to Normalize, display a warning message at the MATLAB command line.
- Error — Stop the simulation and display an error message at the MATLAB command line.

References

[1] Kabal, P. and Ramachandran, R. “The Computation of Line Spectral Frequencies Using Chebyshev Polynomials.“IEEE Transactions on Acoustics, Speech, and Signal Processing, Vol. ASSP-34 No. 6, December 1986. pp. 1419-1426.

Extended Capabilities

C/C++ Code Generation
Generate C and C++ code using Simulink® Coder™.

Generated code relies on the memcpy or memset function (string.h) under certain conditions.

Version History

Introduced before R2006a

LPC to LSF/LSP Conversion

Description

Ports

Input

A — Linear prediction coefficients column vector | unoriented vector | matrix

Output

LSP — Line spectral pairs column vector | unoriented vector | matrix

LSFn — Line spectral frequencies normalized in range (0 0.5) column vector | unoriented vector | matrix

LSFr — Line spectral frequencies in range (0 π) column vector | unoriented vector | matrix

Status — Validity status of output scalar | row vector

Dependencies

Parameters

Output — Conversion output LSP in range (-1 1) (default) | LSF normalized in range (0 0.5) | LSF in range (0 pi)

Root finding coarse grid points — Number of search steps 64 (default) | positive integer greater than 1

Root finding bisection refinement — Number of bisections 4 (default) | nonnegative integer

Show output validity status — Show status of output validity off (default) | on

If current output is invalid, overwrite with previous output — Overwrite invalid outputs with previous output off (default) | on

When first output is invalid, overwrite with user-defined values — Overwrite invalid first output with user-defined values off (default) | on

Dependencies

User-defined LSP/LSF values for overwriting invalid first output — User-defined LSP/LSF values vector (default) | matrix

Dependencies

If first input value is not 1 — Action to take if first input value is not 1 Ignore (default) | Normalize | Normalize and warn | Error

Block Characteristics

More About

LSF and LSP Computation Method: Chebyshev Polynomial Method for Root Finding

Root Finding Method

Root Finding Method Limitations: Failure to Find Roots

Requirements for Valid Outputs

Setting Outputs to LSFs or LSPs

Adjusting Output Computation Time and Accuracy with Root Finding Parameters

Notable Input and Output Properties

Handling and Recognizing Invalid Inputs and Outputs

What Invalid Outputs Look Like

Parameters for Handling Invalid Inputs and Outputs

References

Extended Capabilities

C/C++ Code Generation Generate C and C++ code using Simulink® Coder™.

Version History

See Also

Functions

Blocks

A — Linear prediction coefficients
column vector | unoriented vector | matrix

LSP — Line spectral pairs
column vector | unoriented vector | matrix

LSFn — Line spectral frequencies normalized in range (0 0.5)
column vector | unoriented vector | matrix

LSFr — Line spectral frequencies in range (0 π)
column vector | unoriented vector | matrix

Status — Validity status of output
scalar | row vector

Output — Conversion output
`LSP in range (-1 1)` (default) | `LSF normalized in range (0 0.5)` | `LSF in range (0 pi)`

Root finding coarse grid points — Number of search steps
`64` (default) | positive integer greater than 1

Root finding bisection refinement — Number of bisections
`4` (default) | nonnegative integer

Show output validity status — Show status of output validity
`off` (default) | `on`

If current output is invalid, overwrite with previous output — Overwrite invalid outputs with previous output
`off` (default) | `on`

When first output is invalid, overwrite with user-defined values — Overwrite invalid first output with user-defined values
`off` (default) | `on`

User-defined LSP/LSF values for overwriting invalid first output — User-defined LSP/LSF values
vector (default) | matrix

If first input value is not 1 — Action to take if first input value is not 1
`Ignore` (default) | `Normalize` | `Normalize and warn` | `Error`

C/C++ Code Generation
Generate C and C++ code using Simulink® Coder™.