mfilt.cicinterp

(Removed) Fixed-point CIC interpolator

mfilt.cicinterp has been removed. Use dsp.CICInterpolator instead. For more details, see Version History.

Syntax

hm = mfilt.cicinterp(R,M,N,ILW,OWL,WLPS) hm = mfilt.cicinterp hm = mfilt.cicinterp(R,...)

Description

hm = mfilt.cicinterp(R,M,N,ILW,OWL,WLPS) constructs a cascaded integrator-comb (CIC) interpolation filter object that uses fixed-point arithmetic.

All of the input arguments are optional. To enter any optional value, you must include all optional values to the left of your desired value.

When you omit one or more input options, the omitted option applies the default values shown in the table below.

The following table describes the input arguments for creating hm.

Input Arguments	Description
`R`	Interpolation factor applied to the input signal. Sharpens the response curve to let you change the shape of the response. `R` must be an integer value greater than or equal to 1. The default value is 2.
`M`	Differential delay. Changes the shape, number, and location of nulls in the filter response. Increasing `M` increases the sharpness of the nulls and the response between nulls. In practice, differential delay values of 1 or 2 are the most common. `M` must be an integer value greater than or equal to 1. The default value is 1.
`N`	Number of sections. Deepens the nulls in the response curve. Note that this is the number of either comb or integrator sections, not the total section count. By default, the filter has two sections.
`IWL`	Word length of the input signal. Use any integer number of bits. The default value is 16 bits.
`OWL`	Word length of the output signal. It can be any positive integer number of bits. By default, `OWL` is 16 bits.
`WLPS`	Defines the number of bits per word in each filter section while accumulating the data in the integrator sections or while subtracting the data during the comb sections (using 'wrap' arithmetic). Enter `WLPS` as a scalar or vector of length 2*`N`, where `N` is the number of sections. When `WLPS` is a scalar, the scalar value is applied to each filter section. The default is 16 for each section in the integrator. When you elect to specify `wlps` as an input argument, the `FilterInternals` property automatically switches from the default value of `'FullPrecision'` to `'SpecifyWordLengths'`.

hm = mfilt.cicinterp constructs the CIC interpolator using the default values for the optional input arguments.

hm = mfilt.cicinterp(R,...) constructs the CIC interpolator applying the values you provide for R and any other values you specify as input arguments.

Constraints and Conversions

In Hogenauer [1], the author describes the constraints on CIC interpolator filters. mfilt.cicinterp enforces a constraint—the word lengths of the filter sections must be non-decreasing. That is, the word length of each filter section must be the same size as, or greater than, the word length of the previous filter section.

The formula for W_j, the minimum register width, is derived in [1]. The formula for W_j is given by

$W_{j} = c e i l (B_{i n} + \log_{2} G_{j})$

where G_j, the maximum register growth up to the jth section, is given by

$G_{j} = {\begin{array}{l} 2^{j}, & j = 1, 2, \dots, N \\ \frac{2^{2 N - j} {(R M)}^{j - N}}{R}, & j = N + 1, \dots, 2 N \end{array}$

When the differential delay, M, is 1, there is also a special condition for the register width of the last comb, W_N, that is given by

$\begin{matrix} W_{N} = B_{i n} + N - 1 & i f & M = 1 \end{matrix}$

The conversions denoted by the cast blocks in the integrator diagrams in Algorithms perform the changes between the word lengths of each section. When you specify word lengths that do not follow the constraints described in this section, mfilt.cicinterp returns an error.

The fraction lengths and scalings of the filter sections do not change. At each section the word length is either staying the same or increasing. The signal scaling can change at the output after the final filter section if you choose the output word length to be less than the word length of the final filter section.

Properties of the Object

The following table lists the properties for the filter with a description of each.

Name	Values	Default	Description
`Arithmetic`	`fixed`	`fixed`	Reports the kind of arithmetic the filter uses. CIC interpolators are always fixed-point filters.
`InterpolationFactor`	Any positive integer	2	Amount to increase the input sampling rate.
`DifferentialDelay`	Any positive integer	1	Sets the differential delay for the filter. Usually a value of one or two is appropriate.
`FilterStructure`	`mfilt` structure	None	Reports the type of filter object, such as an interpolator or fractional integrator. You cannot set this property — it is always read only and results from your choice of `mfilt` objects.
`FilterInternals`	`FullPrecision`, `MinWordLengths`, `SpecifyWordLengths`, `SpecifyPrecision`	`FullPrecision`	Set the usage mode for the filter. Refer to Usage Modes below for details.
`InputFracLength`	Any positive integer	16	The number of bits applied as the fraction length to interpret the input data to the filter.
`InputWordLength`	Any positive integer	16	The number of bits applied to the word length to interpret the input data to the filter.
`NumberOfSections`	Any positive integer	2	Number of sections used in the interpolator. Generally called `n`. Reflects either the number of interpolator or comb sections, not the total number of sections in the filter.
`OutputFracLength`	Any positive integer	15	The number of bits applied to the fraction length to interpret the output data from the filter. Read-only.
`OutputWordLength`	Any positive integer	16	The number of bits applied to the word length to interpret the output data from the filter.
`PersistentMemory`	`false` or `true`	`false`	Determines whether the filter states get restored to their starting values for each filtering operation. The starting values are the values in place when you create the filter if you have not changed the filter since you constructed it. `PersistentMemory` returns to zero any state that the filter changes during processing. States that the filter does not change are not affected. When `PersistentMemory` is `false`, you cannot access the filter states. Setting `PersistentMemory` to `true` reveals the `States` property so you can modify the filter states.
`SectionWordLengths`	Any integer or a vector of length 2^N, where N is a positive integer. This property only applies when the `FilterInternals` is `SpecifyWordLengths`.	16	Defines the bits per section used while accumulating the data in the integrator sections or while subtracting the data during the comb sections (using 'wrap' arithmetic). Enter `SectionWordLengths` as a scalar or vector of length 2*`n`, where `n` is the number of sections. When `SectionWordLengths` is a scalar, the scalar value is applied to each filter section. When `SectionWordLengths` is a vector of values, the values apply to the sections in order. The default is 16 for each section in the interpolator. Available when `FilterInternals` is `'SpecifyWordLengths'`.
`States`	`filtstates.cic` object	`m`+1-by-`n` matrix of zeros, after you call function `int`.	Stored conditions for the filter, including values for the integrator and comb sections before and after filtering. `m` is the differential delay of the comb section and `n` is the number of sections in the filter. The integrator states are stored in the first matrix row. States for the comb section fill the remaining rows in the matrix. Available for modification when `PersistentMemory` is `true`. Refer to the `filtstates` object in Signal Processing Toolbox™ documentation for more general information about the `filtstates` object.

Usage Modes

There are usage modes which are set using the FilterInternals property:

FullPrecision — In this mode, the word and fraction lengths of the filter sections and outputs are automatically selected for you. The output and last section word lengths are set to:

$wordlength = ceil (\log_{2} ({(R M)}^{N} / R)) + I,$
where R is the interpolation factor, M is the differential delay, N is the number of filter sections, and I denotes the input word length.
MinWordLengths — In this mode, you specify the word length of the filter output in the OutputWordLength property. The word lengths of the filter sections are automatically set in the same way as in the FullPrecision mode. The section fraction lengths are set to the input fraction length. The output fraction length is set to the input fraction length minus the difference between the last section and output word lengths.
SpecifyWordLengths — In this mode, you specify the word lengths of the filter sections and output in the SectionWordLengths and OutputWordLength properties. The fraction lengths of the filter sections are set such that the spread between word length and fraction length is the same as in full-precision mode. The output fraction length is set to the input fraction length minus the difference between the last section and output word lengths.
SpecifyPrecision — In this mode, you specify the word and fraction lengths of the filter sections and output in the SectionWordLengths, SectionFracLengths, OutputWordLength, and OutputFracLength properties.

About the States of the Filter

In the states property you find the states for both the integrator and comb portions of the filter. states is a matrix of dimensions m+1-by-n, with the states apportioned as follows:

States for the integrator portion of the filter are stored in the first row of the state matrix.
States for the comb portion fill the remaining rows in the state matrix.

To review the states of a CIC filter, use the int method to assign the states. As an example, here are the states for a CIC interpolator hm before and after filtering data:

x = fi(cos(pi/4*[0:99]),true,16,0); % Fixed-point input data
hm = mfilt.cicinterp(2,1,2,16,16,16);
% get initial states-all zero
sts=int(hm.states)
set(hm,'InputFracLength',0); % Integer input specified
y=filter(hm,x);
sts=int(hm.states)
%sts =
%
%     -1     -1
%     -1     -1

Design Considerations

When you design your CIC interpolation filter, remember the following general points:

The filter output spectrum has nulls at ω = k * 2π/rm radians, k = 1,2,3....
Aliasing and imaging occur in the vicinity of the nulls.
n, the number of sections in the filter, determines the passband attenuation. Increasing n improves the filter ability to reject aliasing and imaging, but it also increases the droop or rolloff in the filter passband. Using an appropriate FIR filter in series after the CIC interpolation filter can help you compensate for the induced droop.
The DC gain for the filter is a function of the interpolation factor. Raising the interpolation factor increases the DC gain.

Examples

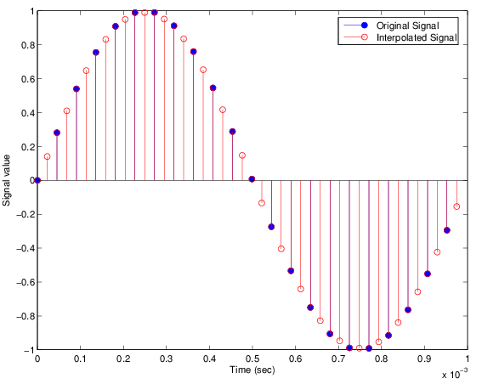
Demonstrate interpolation by a factor of two, in this case from 22.05 kHz to 44.1 kHz. Note the scaling required to see the results in the stem plot and to use the full range of the int16 data type.

R = 2;                      % Interpolation factor.
hm = mfilt.cicinterp(R);    % Use default NumberOfSections and 
                            % DifferentialDelay property values.
fs = 22.05e3;               % Original sample frequency:22.05 kHz.
n = 0:5119;                % 5120 samples, .232 second long signal.
x = sin(2*pi*1e3/fs*n);    % Original signal, sinusoid at 1 kHz.

y_fi = filter(hm,x); % 5120 samples, still 0.232 seconds.
  
% Scale the output to overlay stem plots correctly.
x = double(x);
y = double(y_fi);
y = y/max(abs(y));
stem(n(1:22)/fs,x(1:22),'filled'); % Plot original signal sampled 
                                   % at 22.05 kHz.
hold on;
stem(n(1:44)/(fs*R),y(4:47),'r');  % Plot interpolated signal 
                                   % (44.1 kHz) in red.
xlabel('Time (sec)');ylabel('Signal Value');

As you expect, the plot shows that the interpolated signal matches the input sine shape, with additional samples between each original sample.

Use the filter visualization tool (FVTool) to plot the response of the interpolator object. For example, to plot the response of an interpolator with an interpolation factor of 7, 4 sections, and 1 differential delay, do something like the following:

hm = mfilt.cicinterp(7,1,4)
fvtool(hm)

Algorithms

To show how the CIC interpolation filter is constructed, the following figure presents a block diagram of the filter structure for a two-section CIC interpolation filter (n = 2). fs is the high sampling rate, the output from the interpolation process.

For details about the bits that are removed in the integrator section, refer to [1] in References.

When you select MinWordLengths, the filter section word lengths are automatically set to the minimum number of bits possible in a valid CIC interpolator. mfilt.cicinterp computes the wordlength for each section so the roundoff noise introduced by all sections is less than the roundoff noise introduced by the quantization at the output.

References

[1] Hogenauer, E. B., “An Economical Class of Digital Filters for Decimation and Interpolation,” IEEE^® Transactions on Acoustics, Speech, and Signal Processing, ASSP-29(2): pp. 155-162, 1981

[2] Meyer-Baese, Uwe, “Hogenauer CIC Filters,” in Digital Signal Processing with Field Programmable Gate Arrays, Springer, 2001, pp. 155-172

[3] Harris, Fredric J., Multirate Signal Processing for Communication Systems, Prentice-Hall PTR, 2004 , pp. 343

dsp.CICInterpolator

Version History

Introduced in R2011a

collapse all

R2022a: `mfilt.cicinterp` has been removed

mfilt.cicinterp has been removed. Use dsp.CICInterpolator instead.

Update Code

This table shows how the mfilt.cicinterp object is typically used and explains how to update existing code to use the dsp.CICInterpolator object.

Discouraged Usage Recommended Replacement

Discouraged Usage	Recommended Replacement
Initialize the object. Set the interpolation factor to 2. Uses default `NumSections` = 2, `DifferentialDelay` = 1. hm = mfilt.cicinterp(2); To support frame-based processing, set `PersistentMemory` to `true`. This property retains the state of the filter. hm.PersistentMemory = true; Create fixed-point sinusoidal input signal. Original sample rate is 22.05 kHz. The signal has 512 samples and is 0.0113 seconds long. Fs = 22.05e3; n = (0:511)'; x = fi(sin(2pi1e3/Fs*n),true,16,15); SigIn = dsp.SignalSource(x,32); Process the input signal. The interpolated output has 64 samples per frame. K = 6; % Number of frames y_mfilt = zeros(64,K); for jj=1:K u = SigIn(); y_mfilt(:,jj) = filter(hm,u); end	Initialize the object. Set the interpolation factor to 2. Uses default `NumSections` = 2, `DifferentialDelay` = 1. CICInterp = dsp.CICInterpolator(2); Create fixed-point sinusoidal input signal. Original sample rate is 22.05 kHz. The signal has 512 samples and is 0.0113 seconds long. Fs = 22.05e3; n = (0:511)'; x = fi(sin(2pi1e3/Fs*n),true,16,15); SigIn = dsp.SignalSource(x,32); Process the input signal. The interpolated output has 64 samples per frame. K = 6; y = zeros(64,K); for jj=1:K u = SigIn(); y(:,jj) = CICInterp(u); end

Initialize the object. Set the interpolation factor to 2. Uses default NumSections = 2, DifferentialDelay = 1.

hm = mfilt.cicinterp(2);

To support frame-based processing, set PersistentMemory to true. This property retains the state of the filter.

hm.PersistentMemory = true;

Create fixed-point sinusoidal input signal. Original sample rate is 22.05 kHz. The signal has 512 samples and is 0.0113 seconds long.

Fs = 22.05e3;             
n = (0:511)';                
x = fi(sin(2*pi*1e3/Fs*n),true,16,15);     
SigIn = dsp.SignalSource(x,32);

Process the input signal. The interpolated output has 64 samples per frame.

K = 6; % Number of frames
y_mfilt = zeros(64,K);
for jj=1:K
  u = SigIn();
  y_mfilt(:,jj) = filter(hm,u);
end