mfilt.fftfirinterp

(Removed) Overlap-add FIR polyphase interpolator

mfilt.fftfirinterp has been removed. Use dsp.FIRInterpolator instead. For more details, see Version History.

Syntax

hm = mfilt.fftfirinterp(l,num,bl) hm = mfilt.fftfirinterp hm = mfilt.fftfirinterp(l,...)

Description

hm = mfilt.fftfirinterp(l,num,bl) returns a discrete-time FIR filter object that uses the overlap-add method for filtering input data.

The input arguments are optional. To enter any optional value, you must include all optional values to the left of your desired value.

When you omit one or more input options, the omitted option applies the default values shown in the table below.

The number of FFT points is given by [bl+ceil(length(num)/l)-1]. It is to your advantage to choose bl such that the number of FFT points is a power of two—using powers of two can improve the efficiency of the FFT and the associated interpolation process.

Input Arguments

The following table describes the input arguments for creating hm.

Input Argument	Description
`l`	Interpolation factor for the filter. `l` specifies the amount to increase the input sampling rate. It must be an integer. When you do not specify a value for `l` it defaults to 2.
`num`	Vector containing the coefficients of the FIR lowpass filter used for interpolation. When `num` is not provided as an input, `fftfirinterp` uses a lowpass Nyquist filter with gain equal to `l` and cutoff frequency equal to π`/l` by default.
`bl`	Length of each block of input data used in the filtering. `bl` must be an integer. When you omit input `bl`, it defaults to 100

hm = mfilt.fftfirinterp constructs the filter using the default values for l, num, and bl.

hm = mfilt.fftfirinterp(l,...) constructs the filter using the input arguments you provide and defaults for the argument you omit.

mfilt.fftfirinterp Object Properties

Every multirate filter object has properties that govern the way it behaves when you use it. Note that many of the properties are also input arguments for creating mfilt.fftfirinterp objects. The next table describes each property for an mfilt.fftfirinterp filter object.

Name	Values	Description
`FilterStructure`		Reports the type of filter object. You cannot set this property — it is always read only and results from your choice of `mfilt` object.
`Numerator`		Vector containing the coefficients of the FIR lowpass filter used for interpolation.
`InterpolationFactor`		Interpolation factor for the filter. It specifies the amount to increase the input sampling rate. It must be an integer.
`BlockLength`		Length of each block of input data used in the filtering.
`PersistentMemory`	`false` or `true`	Determines whether the filter states are restored to their starting values for each filtering operation. The starting values are the values in place when you create the filter if you have not changed the filter since you constructed it. `PersistentMemory` returns to zero any state that the filter changes during processing. States that the filter does not change are not affected.
`States`		Stored conditions for the filter, including values for the interpolator states.

Examples

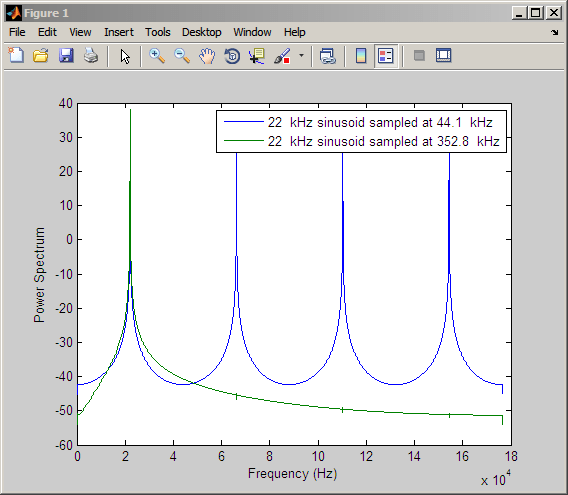
Interpolation by a factor of 8. This object removes the spectral replicas in the signal after interpolation.

l = 8;                        % Interpolation factor
hm = mfilt.fftfirinterp(l);   % We use the default filter
n = 8192;                     % Number of points
hm.blocklength = n;           % Set block length to number of points
fs = 44.1e3;                  % Original sample freq: 44.1 kHz.
n = 0:n-1;                    % 0.1858 secs of data
x = sin(2*pi*n*22e3/fs);      % Original signal, sinusoid at 22 kHz
y = filter(hm,x);             % Interpolated sinusoid
xu = l*upsample(x,8);         % Upsample to compare--the spectrum
                              % does not change
[px,f]=periodogram(xu,[],65536,l*fs);% Power spectrum of original
                                     % signal
[py,f]=periodogram(y,[],65536,l*fs); % Power spectrum of
                                     % interpolated signal
plot(f,10*log10(([fs*px,l*fs*py])))
legend('22  kHz sinusoid sampled at 44.1  kHz',...
'22  kHz sinusoid sampled at 352.8  kHz')
xlabel('Frequency (Hz)'); ylabel('Power Spectrum');

To see the results of the example, look at this figure.

Version History

Introduced in R2011a

collapse all

R2022a: `mfilt.fftfirinterp` has been removed

mfilt.fftfirinterp has been removed. Use dsp.FIRInterpolator instead.

Update Code

This table shows how the mfilt.fftfirinterp object is typically used and explains how to update existing code to use the dsp.FIRInterpolator object.

Discouraged Usage	Recommended Replacement
Initialize the object. Set the interpolation factor to 8. L = 8; hm = mfilt.fftfirinterp(L); Create sinusoidal data and pass the data through the object. % Number of points n = 8192; % Set block length to number of points hm.blocklength = n; % Original sample rate fs = 44.1e3; % 0.1858 secs of data n = (0:n-1)'; % Original signal, sinusoid at 22 kHz x = sin(2pin*22e3/fs); y_mfilt = filter(hm,x);	Initialize the object. Set the interpolation factor to 8. L = 8; firI = dsp.FIRInterpolator(L) Create sinusoidal data and pass the data through the object. % Number of points n = 8192; % Original sample rate fs = 44.1e3; % 0.1858 secs of data n = (0:n-1)'; % Original signal, sinusoid at 22 kHz x = sin(2pin*22e3/fs); y = firI(x);

Discouraged Usage

Recommended Replacement

Initialize the object. Set the interpolation factor to 8.

L = 8;                        
hm = mfilt.fftfirinterp(L);

Create sinusoidal data and pass the data through the object.

% Number of points   
n = 8192;       
% Set block length to number of points            
hm.blocklength = n;  
% Original sample rate         
fs = 44.1e3; 
% 0.1858 secs of data                 
n = (0:n-1)';     
% Original signal, sinusoid at 22 kHz              
x = sin(2*pi*n*22e3/fs);      
y_mfilt = filter(hm,x);