mfilt.holdinterp

(Removed) FIR hold interpolator

mfilt.holdinterp has been removed. Use dsp.FIRInterpolator(L,'ZOH') instead. For more details, see Version History.

Syntax

hm = mfilt.holdinterp(l)

Description

hm = mfilt.holdinterp(l) returns the object hm that represents a hold interpolator with the interpolation factor l. To work, l must be an integer. When you do not include l in the calling syntax, it defaults to 2. To perform interpolation by noninteger amounts, use one of the fractional interpolator objects, such as mfilt.firsrc.

When you use this hold interpolator, each sample added to the input signal between existing samples has the value of the most recent sample from the original signal. Thus you see something like a staircase profile where the interpolated samples form a plateau between the previous and next original samples. The example demonstrates this profile clearly. Compare this to the interpolation process for other interpolators in the toolbox, such as mfilt.linearinterp.

Make this filter a fixed-point or single-precision filter by changing the value of the Arithmetic property for the filter hm as follows:

To change to single-precision filtering, enter
```
set(hm,'arithmetic','single');
```
To change to fixed-point filtering, enter
```
set(hm,'arithmetic','fixed');
```

Input Arguments

The following table describes the input arguments for creating hm.

Input Argument	Description
`l`	Interpolation factor for the filter. `l` specifies the amount to increase the input sampling rate. It must be an integer. When you do not specify a value for `l` it defaults to 2.

Object Properties

This section describes the properties for both floating-point filters (double-precision and single-precision) and fixed-point filters.

Floating-Point Filter Properties

Every multirate filter object has properties that govern the way it behaves when you use it. Note that many of the properties are also input arguments for creating mfilt.holdinterp objects. The next table describes each property for an mfilt.interp filter object.

Name	Values	Description
`Arithmetic`	`Double`, `single`, `fixed`	Specifies the arithmetic the filter uses to process data while filtering.
`FilterStructure`	Character vector	Reports the type of filter object. You cannot set this property — it is always read only and results from your choice of `mfilt` object.
`InterpolationFactor`	Integer	Interpolation factor for the filter. `l` specifies the amount to increase the input sampling rate. It must be an integer.
`PersistentMemory`	'`false`' or '`true`'	Determines whether the filter states are restored to zero for each filtering operation.
`States`	Double or single array	Filter states. `states` defaults to a vector of zeros that has length equal to `nstates` (`hm`). Always available, but visible in the display only when `PersistentMemory` is true.

Fixed-Point Filter Properties

This table shows the properties associated with the fixed-point implementation of the mfilt.holdinterp filter.

Note

The table lists all of the properties that a fixed-point filter can have. Many of the properties listed are dynamic, meaning they exist only in response to the settings of other properties. To view all of the characteristics for a filter at any time, use

info(hm)

where hm is a filter.

For further information about the properties of this filter or any mfilt object, refer to Multirate Filter Properties.

Name	Values	Description
`Arithmetic`	`Double`, `single`, `fixed`	Specifies the arithmetic the filter uses to process data while filtering.
`FilterStructure`	Character vector	Reports the type of filter object. You cannot set this property — it is always read only and results from your choice of `mfilt` object.
`InputFracLength`	Any positive or negative integer number of bits [15]	Specifies the fraction length the filter uses to interpret input data.
`InputWordLength`	Any integer number of bits [16]	Specifies the word length applied to interpret input data.
`InterpolationFactor`	Integer	Interpolation factor for the filter. `l` specifies the amount to increase the input sampling rate. It must be an integer.
`PersistentMemory`	`'false'` or `'true'`	Determine whether the filter states get restored to zero for each filtering operation
`States`	`fi` object	Contains the filter states before, during, and after filter operations. For hold interpolators, the states are always empty — hold interpolators do not have states. The states use `fi` objects, with the associated properties from those objects. For details, refer to fixed-point objects in Fixed-Point Designer™ documentation.

Filter Structure

Hold interpolators do not have filter coefficients and their filter structure is trivial.

Examples

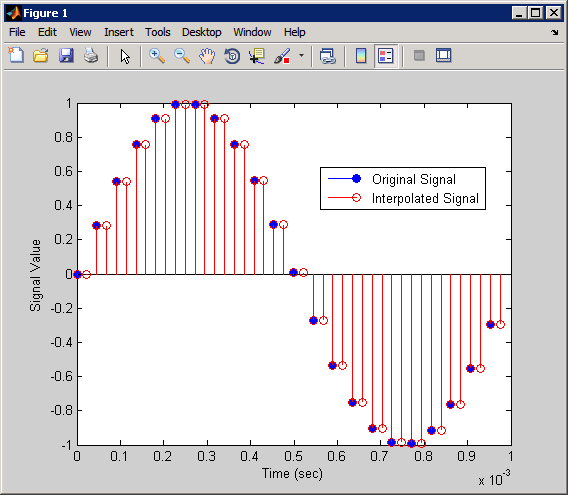
To see the effects of hold-based interpolation, interpolate an input sine wave from 22.05 to 44.1 kHz. Note that each added sample retains the value of the most recent original sample.

l = 2;                              % Interpolation factor
hm = mfilt.holdinterp(l);
fs = 22.05e3;                       % Original sample freq: 22.05 kHz.
n = 0:5119;                         % 5120 samples, 0.232 second long signal
x  = sin(2*pi*1e3/fs*n);            % Original signal, sinusoid at 1 kHz
y = filter(hm,x);                   % 10240 samples, still 0.232 seconds
stem(n(1:22)/fs,x(1:22),'filled')   % Plot original sampled at
                                    % 22.05 kHz
hold on                             % Plot interpolated signal (44.1 kHz)
stem(n(1:44)/(fs*l),y(1:44),'r')
legend('Original Signal','Interpolated Signal','Location','best');
xlabel('Time (sec)');ylabel('Signal Value')

The following figure shows clearly the step nature of the signal that comes from interpolating the signal using the hold algorithm approach. Compare the output to the linear interpolation used in mfilt.linearinterp.

Version History

Introduced in R2011a

collapse all

R2022a: `mfilt.holdinterp` has been removed

mfilt.holdinterp has been removed. Use dsp.FIRInterpolator(L,'ZOH') instead.

Update Code

This table shows how the mfilt.holdinterp object is typically used and explains how to update existing code to use the dsp.FIRInterpolator object.

Discouraged Usage	Recommended Replacement
Initialize the object. Set the interpolation factor to 2. L = 2; hm = mfilt.holdinterp(L); Create a sinusoidal data and pass the data through the object. % Original sample rate is 22.05 kHz fs = 22.05e3; % 5120 samples, 0.232 second long signal n = (0:5119)'; % Original signal, sinusoid at 1 kHz x = sin(2pi1e3/fs*n); % 10240 samples, still 0.232 seconds y_mfilt = filter(hm,x);	Initialize the object. Set the interpolation factor to 2. L = 2; firI = dsp.FIRInterpolator(L,'ZOH') Create a sinusoidal data and pass the data through the object. % Original sample rate is 22.05 kHz fs = 22.05e3; % 5120 samples, 0.232 second long signal n = (0:5119)'; % Original signal, sinusoid at 1 kHz x = sin(2pi1e3/fs*n); % 10240 samples, still 0.232 seconds y = firI(x);

Discouraged Usage

Recommended Replacement

Initialize the object. Set the interpolation factor to 2.

L = 2;                       
hm = mfilt.holdinterp(L);

Create a sinusoidal data and pass the data through the object.

% Original sample rate is 22.05 kHz
fs = 22.05e3;    
% 5120 samples, 0.232 second long signal            
n = (0:5119)';     
% Original signal, sinusoid at 1 kHz             
x  = sin(2*pi*1e3/fs*n);
% 10240 samples, still 0.232 seconds     
y_mfilt = filter(hm,x);