Main Content

RLS Filter

Compute filtered output, filter error, and filter weights for given input and desired signal using RLS adaptive filter algorithm

expand all in page
  • RLS Filter block

Libraries:
DSP System Toolbox / Filtering / Adaptive Filters

Description

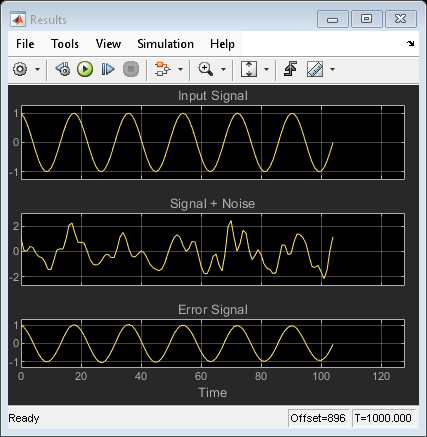
The RLS Filter block recursively computes the least squares estimate (RLS) of the FIR filter weights. The block estimates the filter weights (also known as the coefficients) needed to minimize the error e(n) between the output signal y(n) and the desired signal d(n). For more information, see Algorithms. For more information on adaptive filters, see Overview of Adaptive Filters and Applications.

Examples

Noise Canceler (RLS)

Noise Canceler (RLS)

Subtract noise from an input signal using the Recursive Least Squares (RLS) algorithm. The RLS adaptive filter uses the reference signal on the Input port and the desired signal on the Desired port to automatically match the filter response in the Noise Filter block. As it converges to the correct filter, the filtered noise should be completely subtracted from the "Signal+Noise" signal, and the "Error Signal" should contain only the original signal.

Ports

Input

expand all

Specify the input signal you want to filter as a scalar or a column vector.

The input signal and the desired signal must have the same size, data type, and complexity.

The input signal can be a variable-size signal, that is, the frame length of the signal can change during simulation as long as the signal dimensions match with the input signal.

Data Types: single | double
Complex Number Support: Yes

Specify the signal you want to model as a scalar or a column vector. The RLS filter adapts its coefficients to minimize the error and converge the input signal to the desired signal as closely as possible.

The input signal and the desired signal must have the same size, data type, and complexity.

The desired signal can be a variable-size signal, that is, the frame length of the signal can change during simulation as long as the signal dimensions match with the input signal.

Data Types: single | double
Complex Number Support: Yes

Specify the RLS forgetting factor λ as a scalar in the range 0 ≤ λ ≤ 1 through this input port. For more information on this parameter, see the Forgetting factor (0 to 1) parameter description.

Dependencies

To enable this port, set the Specify forgetting factor via parameter as Input port.

Data Types: single | double

If the input is a nonzero value, the block continuously updates the filter weights. If the value of this input is zero, the filter weights remain at their current values.

Dependencies

To enable this port, select the Adapt port parameter.

Data Types: single | double

Specify the reset signal as a scalar signal. When you want to reset the value of the filter weights to their initial values, use the Reset port parameter. The block resets the filter weights whenever a reset event is detected at the Reset port. The reset signal rate must be the same rate as the data signal input.

To enable the Reset port, select one of these options from the Reset port list:

  • Rising edge — Triggers a reset operation when the Reset input does one of the following:

    • Rises from a negative value to a positive value or zero

    • Rises from zero to a positive value, where the rise is not a continuation of a rise from a negative value to zero

  • Falling edge — Triggers a reset operation when the Reset input does one of the following:

    • Falls from a positive value to a negative value or zero

    • Falls from zero to a negative value, where the fall is not a continuation of a fall from a positive value to zero

  • Either edge — Triggers a reset operation when the Reset input is a Rising edge or Falling edge

  • Non-zero sample — Triggers a reset operation at each sample time that the Reset input is not zero

To disable the reset port, set Reset port to None.

Dependencies

To enable this port, set Reset port to any option other than None.

Data Types: single | double

Output

expand all

Filtered signal, returned as a scalar or a column vector. The block adapts its filter coefficients to converge the input signal to match the desired signal. The filter outputs the converged signal. For more details on how the block computes the output, see Algorithms.

Data Types: single | double
Complex Number Support: Yes

Difference between the filtered signal and the desired signal, returned as a scalar or a column vector. The objective of the RLS filter is to minimize this error. The block adapts its coefficients to converge towards optimal filter coefficients that produce an output signal that matches closely with the desired signal. For more details on how the block computes the error, see Algorithms.

The block outputs the RLS filter coefficients through the Wts port.

Data Types: single | double
Complex Number Support: Yes

Weights of the RLS filter, returned as a column vector of length equal to the value you specify in the Filter length parameter. For each iteration, the block outputs the current updated filter weights from this port. For more information on how the block updates the filter weights, see Algorithms.

The data type of the filter weights matches the data type of the filtered signal.

Dependencies

To enable this port, select the Output filter weights parameter.

Data Types: single | double
Complex Number Support: Yes

Parameters

expand all

Specify the length of the FIR filter coefficients vector L as a positive integer.

Specify the forgetting factor through:

  • Dialog –– Use the Forgetting factor (0 to 1) parameter to specify the forgetting factor in the block dialog box.

  • Input port –– Use the Lambda input port to specify the forgetting factor.

Specify the RLS forgetting factor λ as a scalar in the range 0 ≤ λ ≤ 1. This parameter specifies how quickly the filter forgets past sample information. Setting λ = 1 denotes infinite memory, while adapting to find the new filter. Typically, 1−12L<λ<1, where L is the filter length. You can specify a forgetting factor using the input port, Lambda, or enter a value in the Forgetting factor (0 to 1) parameter in the block dialog box.

Tunable: Yes

Dependencies

To enable this parameter, set the Specify forgetting factor via parameter to Dialog.

Specify initial values of the FIR filter weights w^(0) as a scalar or a vector of length equal to the filter length. When you specify a scalar, the block uses the scalar value to create a vector of filter weights. This vector has length equal to the filter length and all of its values are equal to the scalar value.

Specify the initial values of the input covariance estimate, 1/P(n) as a:

  • Scalar –– P(n) is a diagonal matrix with diagonal elements equal to the scalar value.

  • Square matrix –– Each dimension of the matrix equals the value you specify in the Filter length parameter.

The initial value of P(n) is 1σ2I where you specify σ2 in the Initial input variance estimate parameter.

Select this parameter to enable the Adapt input port. Use this port to specify if the block must update its filter weights or to keep them at the current level. For more information, see the description of the Adapt input port.

Select this parameter to enable the Reset input port. For more information on each of the reset options, see the description for the Reset input port.

Select this parameter to export the filter weights from the Wts port.

Block Characteristics

Data Types

double | single

Multidimensional Signals

No

Variable-Size Signals

No

Algorithms

The RLS filter is expressed in matrix form as

k(n)=λ−1P(n−1)u(n)1+λ−1uH(n)P(n−1)u(n)y(n)=w(n−1)u(n)e(n)=d(n)−y(n)w(n)=w(n−1)+kH(n)e(n)P(n)=λ−1P(n−1)−λ−1k(n)uH(n)P(n−1)

where λ−1 denotes the reciprocal of the exponential weighting factor.

The variables are as follows:

VariableDescription

n

The current time index

u(n)

The vector of buffered input samples at step n

P(n)

The inverse covariance matrix at step n

k(n)

The gain vector at step n

w(n)

The vector of filter-tap estimates at step n

y(n)

The filtered output at step n

e(n)

The estimation error at step n

d(n)

The desired response at step n

λ

The forgetting factor

The implementation of the algorithm in the block is optimized by exploiting the symmetry of the inverse covariance matrix P(n). This decreases the total number of computations by a factor of two.

References

[1] Hayes, M.H. Statistical Digital Signal Processing and Modeling. New York: John Wiley & Sons, 1996.

Extended Capabilities

Version History

Introduced before R2006a

See Also

Objects

Blocks

Topics