使用 RLS 自适应滤波的自适应降噪
此示例说明如何使用 RLS 滤波器从含噪信号中提取有用信息。承载信息的信号是被加性高斯白噪声破坏的正弦波。
自适应降噪系统假设使用两个麦克风。主麦克风选取含噪输入信号,而辅助麦克风接收与承载信息的信号不相关但与主麦克风选取的噪声相关的噪声。
注意:此示例等效于提供的 Simulink® 模型 rlsdemo。
该模型展示自适应 RLS 滤波器从含噪信号中提取有用信息的能力。

承载信息的信号是 0.055 周期/采样的正弦波。创建承载信息的信号并对其绘图。
signal = sin(2*pi*0.055*(0:1000-1)'); signalSource = dsp.SignalSource(signal,SamplesPerFrame=100,... SignalEndAction="Cyclic repetition"); scope = timescope(YLimits=[-2 2],Title="Information bearing signal")
scope =
timescope handle with properties:
SampleRate: 1
TimeSpanSource: 'auto'
TimeSpanOverrunAction: 'scroll'
AxesScaling: 'manual'
Show all properties
scope(signal(1:200));

辅助麦克风选取的噪声是 RLS 自适应滤波器的输入。破坏正弦波的噪声是该噪声经过低通滤波的版本(与之相关)。滤波后噪声和承载信息的信号之和是自适应滤波器的期望信号。创建含噪信号并对其绘图。
nvar = 1.0; % Noise variance noise = randn(1000,1)*nvar; % White noise noiseSource = dsp.SignalSource(noise,SamplesPerFrame=100,... SignalEndAction="Cyclic repetition"); scope = timescope(YLimits=[-4 4], Title="Noise picked up by the secondary microphone"); scope(noise);

破坏承载信息的信号的噪声是您在上一步骤中创建的含噪信号的经过滤波的版本。初始化对含噪信号进行操作的滤波器。
lp = dsp.FIRFilter('Numerator',fir1(31,0.5));% Low pass FIR filter
设置 RLS 滤波器的参数并初始化该滤波器。
M = 32; % Filter order delta = 0.1; % Initial input covariance estimate P0 = (1/delta)*eye(M,M); % Initial setting for the P matrix rlsfilt = dsp.RLSFilter(M,InitialInverseCovariance=P0);
对 RLS 自适应滤波器运行 1000 次迭代。当自适应滤波器收敛时,滤波后的噪声应完全从信号 + 噪声中减去。误差 e 应仅包含原始信号。
scope = timescope(TimeSpan=1000,YLimits=[-2,2], ... TimeSpanOverrunAction="scroll"); for k = 1:10 n = noiseSource(); % Noise s = signalSource(); d = lp(n) + s; [y,e] = rlsfilt(n,d); scope([s,e]); end release(scope);
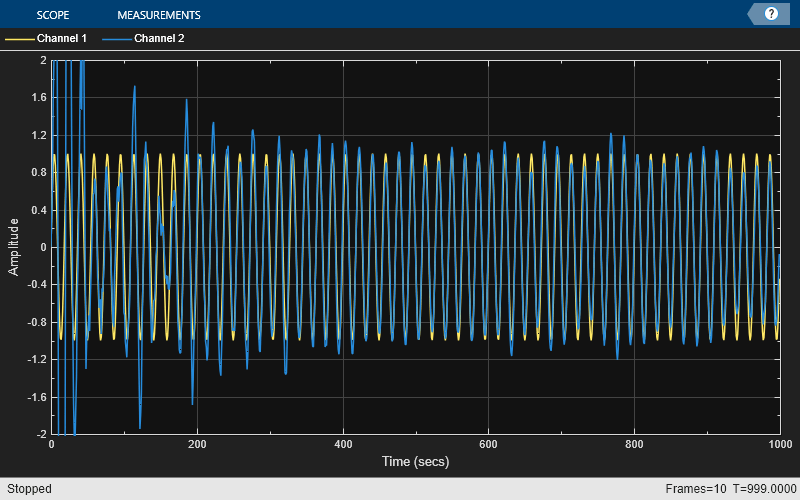
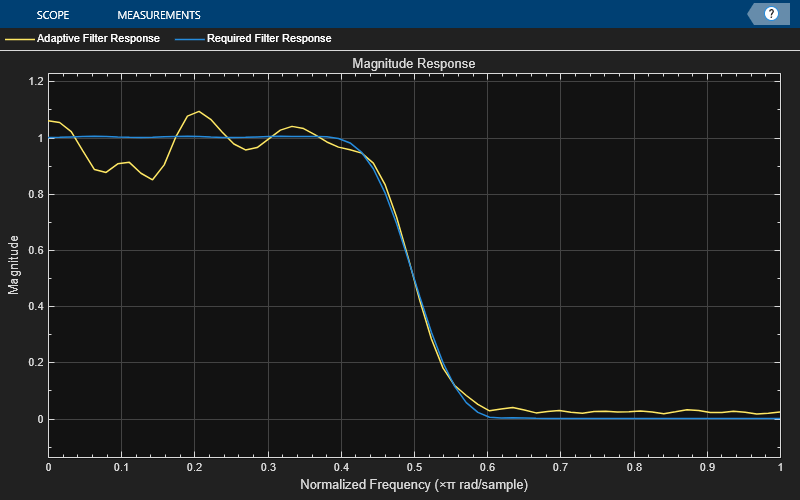
该图显示自适应滤波器响应收敛于 FIR 滤波器的响应。
visualizer = dsp.DynamicFilterVisualizer(64,NormalizedFrequency=true,... MagnitudeDisplay="Magnitude", ... FilterNames=["Adaptive Filter Response","Required Filter Response"]); visualizer(rlsfilt.Coefficients,1,lp.Numerator,1);
参考
[1] S.Haykin, "Adaptive Filter Theory", 3rd Edition, Prentice Hall, N.J., 1996.