dsp.FIRFilter

Static or time-varying FIR filter

Description

The dsp.FIRFilter System object™ filters each channel of the input using static or time-varying FIR filter implementations.

To filter each channel of the input:

Create the dsp.FIRFilter object and set its properties.
Call the object with arguments, as if it were a function.

To learn more about how System objects work, see What Are System Objects?

This object supports C/C++ code generation and SIMD code generation under certain conditions. For more information, see Code Generation.

Creation

Syntax

fir = dsp.FIRFilter

fir = dsp.FIRFilter(num)

fir = dsp.FIRFilter(Name,Value)

Description

fir = dsp.FIRFilter returns a finite impulse response (FIR) filter object, fir, which independently filters each channel of the input over time using a specified FIR filter implementation.

fir = dsp.FIRFilter(num) returns an FIR filter System object, fir, with the Numerator property set to num.

example

fir = dsp.FIRFilter(Name,Value) returns an FIR filter System object, fir, with each property set to the specified value.

Properties

expand all

Unless otherwise indicated, properties are nontunable, which means you cannot change their values after calling the object. Objects lock when you call them, and the release function unlocks them.

If a property is tunable, you can change its value at any time.

For more information on changing property values, see System Design in MATLAB Using System Objects.

`Structure` — Filter structure
`Direct form` (default) | `Direct form symmetric` | `Direct form antisymmetric` | `Direct form transposed` | `Lattice MA`

Specify the filter structure. You can specify the filter structure as one of Direct form | Direct form symmetric | Direct form antisymmetric | Direct form transposed | Lattice MA.

`NumeratorSource` — Source of filter coefficients
`Property` (default) | `Input port`

Specify the source of the filter coefficients as Property or Input port. When you specify Input port, the filter object updates the time-varying filter once every frame.

Dependencies

This applies when you set the Structure to Direct form | Direct form symmetric | Direct form antisymmetric | Direct form transposed.

`ReflectionCoefficientsSource` — Source of filter coefficients
`Property` (default) | `Input port`

Specify the source of the Lattice filter coefficients as Property or Input port. When you specify Input port, the filter object updates the time-varying filter once every frame.

Dependencies

This applies when you set the Structure to Lattice MA.

`Numerator` — Numerator coefficients
`[0.5 0.5]` (default) | row vector

Specify the filter coefficients as a real or complex numeric row vector.

Tunable: Yes

Dependencies

This property applies when you set the NumeratorSource property to Property, and the Structure property is set to Direct form, Direct form symmetric, Direct form antisymmetric, or Direct form transposed.

`ReflectionCoefficients` — Reflection coefficients of lattice filter structure
`[0.5 0.5]` (default) | row vector

Specify the reflection coefficients of a lattice filter as a real or complex numeric row vector.

Tunable: Yes

Dependencies

This property applies when you set the Structure property to Lattice MA, and the ReflectionCoefficientsSource property to Property.

`InitialConditions` — Initial conditions for the FIR filter
`0` (default) | scalar | vector | matrix

Specify the initial conditions of the filter states. The number of states or delay elements equals the number of reflection coefficients for the lattice structure, or the number of filter coefficients–1 for the other direct form structures.

You can specify the initial conditions as a scalar, vector, or matrix. If you specify a scalar value, the FIR filter object initializes all delay elements in the filter to that value. If you specify a vector whose length equals the number of delay elements in the filter, each vector element specifies a unique initial condition for the corresponding delay element. The object applies the same vector of initial conditions to each channel of the input signal.

If you specify a vector whose length equals the product of the number of input channels and the number of delay elements in the filter, each element specifies a unique initial condition for the corresponding delay element in the corresponding channel.

If you specify a matrix with the same number of rows as the number of delay elements in the filter, and one column for each channel of the input signal, each element specifies a unique initial condition for the corresponding delay element in the corresponding channel.

Tunable: Yes

Fixed-Point Properties

`FullPrecisionOverride` — Full precision override for fixed-point arithmetic
`true` (default) | `false`

Specify whether to use full precision rules. If you set FullPrecisionOverride to true, which is the default, the object computes all internal arithmetic and output data types using full precision rules. These rules provide the most accurate fixed-point numerics. It also turns off the display of other fixed-point properties because they do not apply individually. These rules guarantee that no quantization occurs within the object. Bits are added, as needed, to ensure that no roundoff or overflow occurs. If you set FullPrecisionOverride to false, fixed-point data types are controlled through individual fixed-point property settings. For more information, see Full Precision for Fixed-Point System Objects.

`RoundingMethod` — Rounding method for fixed-point operations
`Floor` (default) | `Ceiling` | `Convergent` | `Nearest` | `Round` | `Simplest` | `Zero`

Specify the rounding method.

Dependencies

This property applies only if the object is not in full precision mode.

`OverflowAction` — Overflow action for fixed-point operations
`Wrap` (default) | `Saturate`

Specify the overflow action as Wrap or Saturate.

Dependencies

This property applies only if the object is not in full precision mode.

`CoefficientsDataType` — Coefficients word and fraction lengths
`Same word length as input` (default) | `Custom`

Specify the coefficients fixed-point data type as Same word length as input or Custom.

Dependencies

This property applies when you set the NumeratorSource property to Property.

`CustomCoefficientsDataType` — Custom coefficients word and fraction lengths
`numerictype(true,16,15)` (default) | numerictype

Specify the coefficients fixed-point type as a signed or unsigned numerictype (Fixed-Point Designer) object.

Dependencies

This property applies when you set the CoefficientsDataType property to Custom.

`ReflectionCoefficientsDataType` — Reflection coefficients word and fraction lengths
`Same word length as input` (default) | `Custom`

Specify the reflection coefficients fixed-point data type as Same word length as input or Custom.

Dependencies

This property applies when you set the ReflectionCoefficientsSource property to Property.

`CustomReflectionCoefficientsDataType` — Custom reflection coefficients word and fraction lengths
`numerictype(true,16,15)` (default) | numerictype

Specify the reflection coefficients fixed-point type as a signed or unsigned numerictype (Fixed-Point Designer) object.

Dependencies

This property applies when you set the ReflectionCoefficientsDataType property to Custom.

`ProductDataType` — Product word and fraction lengths
`Full precision` (default) | `Same as input` | `Custom`

Specify the product fixed-point data type as Full precision, Same as input, or Custom.

`CustomProductDataType` — Custom product word and fraction lengths
`numerictype(true,32,30)` (default) | numerictype

Specify the product fixed-point type as a signed or unsigned scaled numerictype (Fixed-Point Designer) object.

Dependencies

This property applies when you set the ProductDataType property to Custom.

`AccumulatorDataType` — Accumulator word and fraction lengths
`Full precision` (default) | `Same as input` | `Same as product` | `Custom`

Specify the accumulator fixed-point data type to Full precision, Same as input, Same as product, or Custom.

`CustomAccumulatorDataType` — Custom accumulator word and fraction lengths
`numerictype(true,32,30)` (default) | numerictype

Specify the accumulator fixed-point type as a signed or unsigned scaled numerictype (Fixed-Point Designer) object.

Dependencies

This property applies when you set the AccumulatorDataType property to Custom.

`StateDataType` — State word and fraction lengths
`Same as accumulator` (default) | `Same as input` | `Custom`

Specify the state fixed-point data type as one of Same as input, Same as accumulator, or Custom.

Dependencies

This property does not apply to any of the direct form or direct form I filter structures.

`CustomStateDataType` — Custom state word and fraction lengths
`numerictype(true,16,15)` (default) | numerictype

Specify the state fixed-point type as a signed or unsigned scaled numerictype (Fixed-Point Designer) object.

Dependencies

This property applies when you set the StateDataType property to Custom.

`OutputDataType` — Output word and fraction lengths
`Same as accumulator` (default) | `Same as input` | `Custom`

Specify the output fixed-point data type as one of Same as input, Same as accumulator, or Custom.

`CustomOutputDataType` — Custom output word and fraction lengths
`numerictype(true,16,15)` (default) | `numerictype`

Specify the output fixed-point type as a signed or unsigned scaled numerictype (Fixed-Point Designer) object.

Dependencies

This property applies when you set the OutputDataType property to Custom.

Usage

Syntax

y = fir(x)

y = fir(x,coeff)

Description

y = fir(x) applies an FIR filter to the real or complex input signal x to produce the output y.

example

y = fir(x,coeff) uses the time-varying coefficients, coeff , to filter the input signal x and produce the output y. You can use this option when you set the NumeratorSource or ReflectionCoefficientsSource property to Input port.

example

Input Arguments

expand all

`x` — Data input
vector | matrix

Data input, specified as a vector or a matrix. When the input data is of a fixed-point type, it must be signed when the structure is set to Direct form symmetric or Direct form antisymmetric. The FIR filter object operates on each channel of the input signal independently over successive calls to the object.

This System object supports variable-size input.

`coeff` — Filter coefficients
row vector

Time-varying filter coefficients, specified as a row vector. The data and coefficient inputs must have the same data type.

Output Arguments

expand all

`y` — Filtered output
vector | matrix

Filtered output, returned as a vector or a matrix. The output has the same size as the input. For single and double inputs, the output data type matches the input data type. For integer and fixed-point inputs, the output data type depends on the setting of the FullPrecisionOverride and OutputDataType properties.

Object Functions

To use an object function, specify the System object as the first input argument. For example, to release system resources of a System object named obj, use this syntax:

release(obj)

expand all

Specific to `dsp.FIRFilter`

`freqz`	Frequency response of discrete-time filter System object
`filterAnalyzer`	Analyze filters with Filter Analyzer app
`impz`	Impulse response of discrete-time filter System object
`info`	Information about filter System object
`coeffs`	Returns the filter System object coefficients in a structure
`cost`	Estimate cost of implementing filter System object
`grpdelay`	Group delay response of discrete-time filter System object
`generatehdl`	Generate HDL code for quantized DSP filter (requires Filter Design HDL Coder) (To be removed)
`outputDelay`	Determine output delay of single-rate or multirate filter

Common to All System Objects

`step`	Run System object algorithm
`release`	Release resources and allow changes to System object property values and input characteristics
`reset`	Reset internal states of System object

Examples

collapse all

Lowpass Filter a Sinusoid Signal Using FIRFilter object

Open Live Script

Use an FIR filter to apply a lowpass filter to a waveform with two sinusoidal components.

 t = (0:1000)'/8e3;
 xin = sin(2*pi*0.3e3*t)+sin(2*pi*3e3*t);
 
 sr = dsp.SignalSource;
 sr.Signal = xin;
 sink = dsp.SignalSink;

 fir = dsp.FIRFilter(designLowpassFIR(FilterOrder=10,CutoffFrequency=0.5));

sa = spectrumAnalyzer(...
     SampleRate=8e3,...
     Method='welch',...
     PlotAsTwoSidedSpectrum=false,...
     OverlapPercent=80,...
     SpectrumUnits='dBW',...
     YLimits=[-150 -10]);

 while ~isDone(sr)
      input = sr();
      filteredOutput = fir(input);
      sink(filteredOutput);
      sa(filteredOutput)
 end

 filteredResult = sink.Buffer;
 filterAnalyzer(fir,SampleRates=8000)

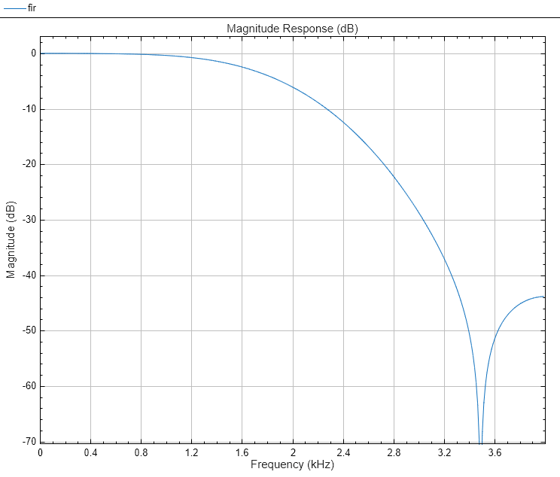
Design an FIR filter as a System object.

N = 10;  
Fc = 0.4;
firFiltObj = designLowpassFIR(FilterOrder=N,CutoffFrequency=Fc,SystemObject=true)

firFiltObj = 
  dsp.FIRFilter with properties:

            Structure: 'Direct form'
      NumeratorSource: 'Property'
            Numerator: [-1.2414e-18 -0.0126 -0.0247 0.0635 0.2748 0.3981 0.2748 0.0635 -0.0247 -0.0126 -1.2414e-18]
    InitialConditions: 0

  Use get to show all properties

filterAnalyzer(firFiltObj)

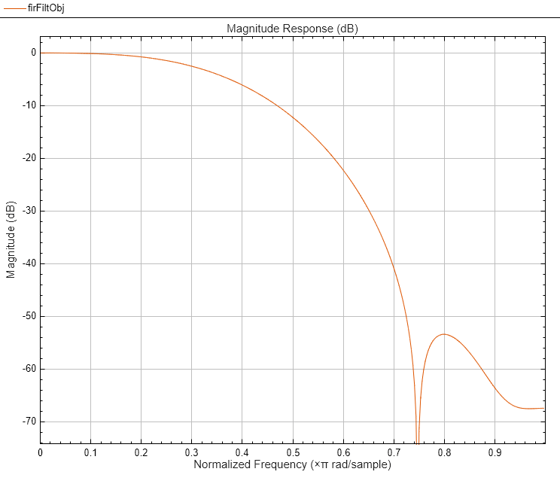
Design and Implement Lowpass FIR Filter with Tunable Cutoff Frequency

Open Live Script

Create a dsp.FIRFilter object, and set the NumeratorSource property to 'Input port' so that you can vary the coefficients of the FIR filter through the input port during simulation.

firFilt = dsp.FIRFilter(NumeratorSource="Input port")

firFilt = 
  dsp.FIRFilter with properties:

            Structure: 'Direct form'
      NumeratorSource: 'Input port'
    InitialConditions: 0

  Use get to show all properties

Create a spectrumAnalyzer object to visualize the spectra of the input and output signals.

spectrumScope = spectrumAnalyzer(SampleRate=44100,PlotAsTwoSidedSpectrum=false,...
    ChannelNames=["Input Signal","Filtered Signal"]);

Create a dsp.DynamicFilterVisualizer object to visualize the magnitude response of the varying filter.

filterViz = dsp.DynamicFilterVisualizer(NormalizedFrequency=true);

Stream in random data and filter the signal using the dsp.FIRFilter object. Use the designLowpassFIR function to design the filter coefficients. By default, this function returns a vector of FIR filter coefficients. Assign these coefficients to the dsp.FIRFilter object.

Vary the cutoff frequency of the filter during simulation. The designLowpassFIR function redesigns the coefficients based on the updated filter specifications. Pass these updated coefficients to the FIR filter. Visualize the spectra of the input and filtered signals using the spectrum analyzer.

Fcut = 0.5;
for idx = 1:500
    num = designLowpassFIR(FilterOrder=30,CutoffFrequency=Fcut,Window="hann");
    x = randn(1024,1);
    y = firFilt(x,num);
    spectrumScope(x,y);
    filterViz(num);
    Fcut = Fcut + 0.0005;
end

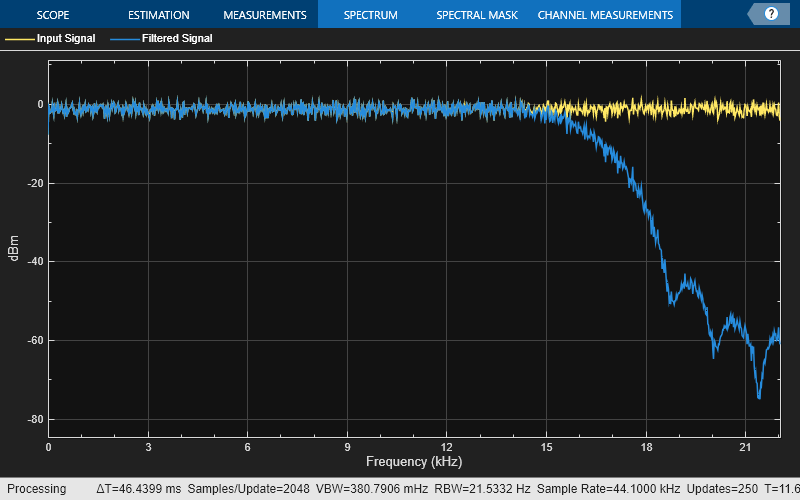
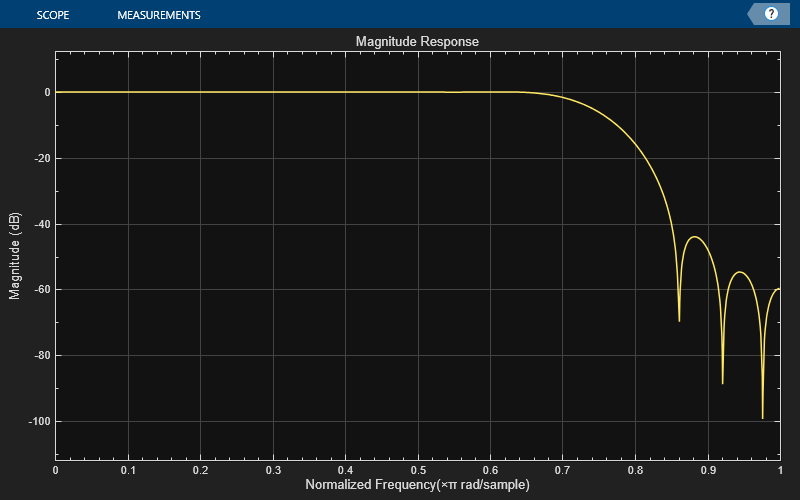
Design and Implement Lowpass FIR Filter Object

Open Live Script

Design and implement a lowpass FIR filter object using the designLowpassFIR function. The function returns a dsp.FIRFilter object when you set the SystemObject argument to true. To design the filter in single-precision, use the Datatype or like argument. Alternatively, you can specify any of the numerical arguments in single-precision.

firFilt = designLowpassFIR(FilterOrder=30,CutoffFrequency=0.5,Window="hann",...
        Datatype="single",SystemObject=true)

firFilt = 
  dsp.FIRFilter with properties:

            Structure: 'Direct form'
      NumeratorSource: 'Property'
            Numerator: [0 2.1297e-19 0.0011 -1.8613e-18 -0.0048 4.8729e-18 0.0122 -8.7270e-18 -0.0251 1.2757e-17 0.0477 -1.6267e-17 -0.0960 1.8649e-17 0.3148 0.5000 0.3148 1.8649e-17 -0.0960 -1.6267e-17 0.0477 1.2757e-17 -0.0251 ... ] (1x31 single)
    InitialConditions: 0

  Use get to show all properties

Create a dsp.DynamicFilterVisualizer object to visualize the magnitude response of the filter.

filterViz = dsp.DynamicFilterVisualizer(NormalizedFrequency=true);
filterViz(firFilt)

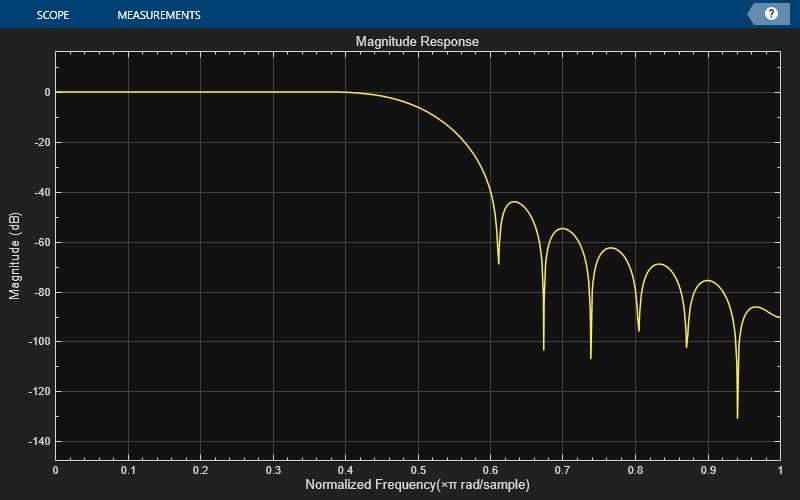
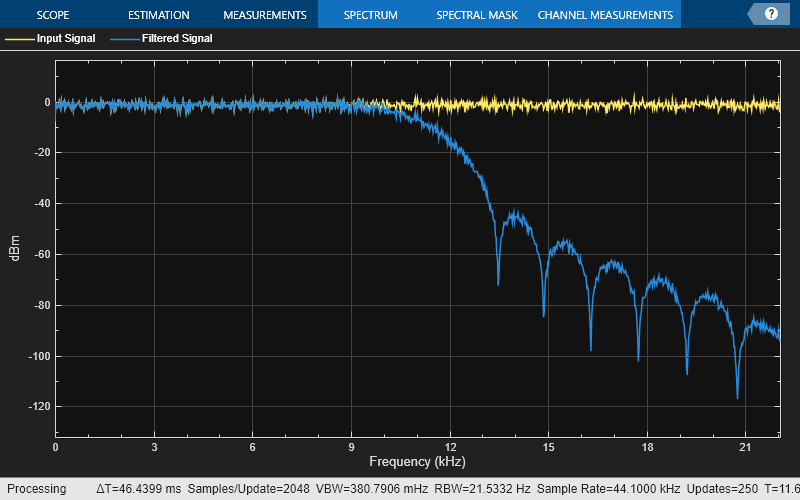
Create a spectrumAnalyzer object to visualize the spectra of the input and output signals.

spectrumScope = spectrumAnalyzer(SampleRate=44100,PlotAsTwoSidedSpectrum=false,...
    ChannelNames=["Input Signal","Filtered Signal"]);

Stream in random data and filter the signal using the dsp.FIRFilter object. Visualize the spectra of the input and filtered signals using the spectrum analyzer.

for idx = 1:500
    x = randn(1024,1);
    y = firFilt(x);
    spectrumScope(x,y);
end

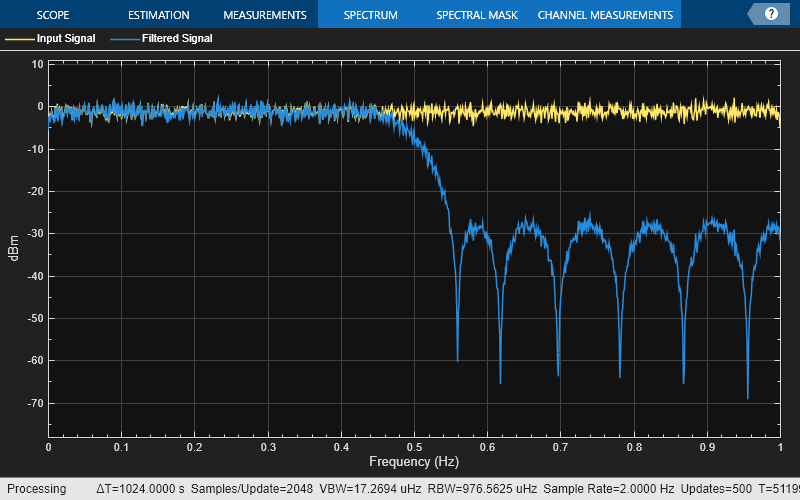
Design and Implement Equiripple FIR Halfband Filter

Open Live Script

Design an equiripple FIR halfband filter with the order of 24 and a transition width of 0.1 using the designHalfbandFIR function. Assign the filter coefficients to a dsp.FIRFilter System object.

b = designHalfbandFIR(FilterOrder=24,DesignMethod='equiripple');
hbFIR = dsp.FIRFilter(b);

Create a dsp.DynamicFilterVisualizer object and visualize the magnitude response of the filter.

dfv = dsp.DynamicFilterVisualizer(NormalizedFrequency=true);
dfv(hbFIR);

Create a spectrumAnalyzer object to visualize the spectra of the input and output signals.

scope = spectrumAnalyzer(SampleRate=2, PlotAsTwoSidedSpectrum=false,...
    ChannelNames=["Input Signal","Filtered Signal"]);

Stream in random data and filter the signal using the FIR halfband filter.

for i = 1:1000
    x = randn(1024, 1);
    y = hbFIR(x);
    scope(x,y);
end

Design Lowpass FIR Filter Using `designfilt`

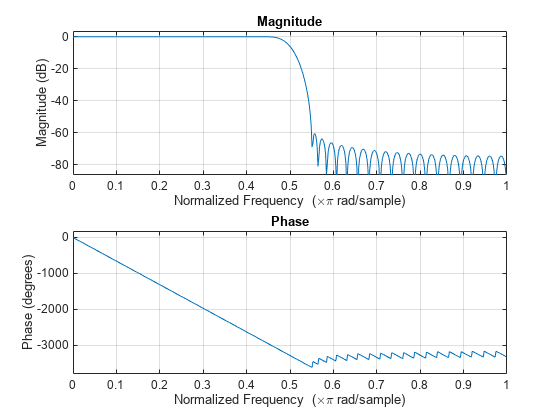
Since R2023b

Open Live Script

Design a lowpass FIR filter using the designfilt function.

The filter is a minimum order filter with a passband frequency of 0.45 and a stopband frequency of 0.55 in normalized frequency units. The passband ripple is 1 dB and the stopband attenuation is 60 dB. Use the Kaiser window design method and set the SystemObject argument to true.

With these specifications, the designfilt function generates a dsp.FIRFilter System object™.

lpFIRFilter = designfilt('lowpassfir', ...
    'PassbandFrequency',0.45,'StopbandFrequency',0.55, ...
    'PassbandRipple',1,'StopbandAttenuation',60, ...
    'DesignMethod','kaiserwin','SystemObject',true)

lpFIRFilter = 
  dsp.FIRFilter with properties:

            Structure: 'Direct form'
      NumeratorSource: 'Property'
            Numerator: [1.2573e-04 -1.9141e-04 -2.7282e-04 3.7207e-04 4.9141e-04 -6.3325e-04 -8.0016e-04 9.9490e-04 0.0012 -0.0015 -0.0018 0.0021 0.0025 -0.0029 -0.0034 0.0040 0.0046 -0.0053 -0.0060 0.0069 0.0079 -0.0090 -0.0102 0.0116 ... ] (1x74 double)
    InitialConditions: 0

  Use get to show all properties

Visualize the magnitude and phase responses of this filter using freqz.

freqz(lpFIRFilter.Numerator)

$Figure contains 2 axes objects. Axes object 1 with title Phase, xlabel Normalized Frequency (\times\pi rad/sample), ylabel Phase (degrees) contains an object of type line. Axes object 2 with title Magnitude, xlabel Normalized Frequency (\times\pi rad/sample), ylabel Magnitude (dB) contains an object of type line.$

Algorithms

This object implements the algorithm, inputs, and outputs described on the Discrete FIR Filter (Simulink) block reference page. The object properties correspond to the block parameters.

Extended Capabilities

C/C++ Code Generation
Generate C and C++ code using MATLAB® Coder™.

Usage notes and limitations:

Only the Numerator property is tunable for code generation.
See System Objects in MATLAB Code Generation (MATLAB Coder).

The dsp.FIRFilter System object supports SIMD code generation using Intel^® AVX2 code replacement library under these conditions:

Filter structure is set to 'Direct form' or 'Direct form transposed'.
Input signal is real-valued with real filter coefficients.
When the filter structure is set to 'Direct form', the input signal can also be complex-valued with real or complex filter coefficients.
Input signal has a data type of single or double.

The SIMD technology significantly improves the performance of the generated code. For more information, see SIMD Code Generation. To generate SIMD code from this object, see Use Intel AVX2 Code Replacement Library to Generate SIMD Code from MATLAB Algorithms.

HDL Code Generation
Generate VHDL, Verilog and SystemVerilog code for FPGA and ASIC designs using HDL Coder™.

This object supports HDL code generation with the HDL Coder™ or Filter Design HDL Coder™ products. For HDL Coder workflow and limitations, see HDL Code Generation for System Objects (HDL Coder). For Filter Design HDL Coder workflow and limitations, see Generate HDL Code for Filter System Objects (Filter Design HDL Coder).

Version History

Introduced in R2012a

expand all

R2023b: The `designfilt` function and the Design Filter Live Editor task support `dsp.FIRFilter` object

The designfilt function generates a dsp.FIRFilter object when you specify 'lowpassfir' and 'highpassfir' filter responses and set the 'SystemObject' flag to 'true'.

lpFIRFilter = designfilt('lowpassfir', ...
    'PassbandFrequency',0.45,'StopbandFrequency',0.55, ...
    'PassbandRipple',1,'StopbandAttenuation',60, ...
    'DesignMethod','kaiserwin','SystemObject',true)

lpFIRFilter = 
  dsp.FIRFilter with properties:

            Structure: 'Direct form'
      NumeratorSource: 'Property'
            Numerator: [1.2573e-04 -1.9141e-04 -2.7282e-04 3.7207e-04 … ] (1×74 double)
    InitialConditions: 0

The Design Filter Live Editor task generates a dsp.FIRFilter object for lowpass FIR and highpass FIR filter responses when you select the Use a System object to implement filter check box in the task UI and run the designfilt code the task generates.

dsp.FIRFilter

Description

Creation

Syntax

Description

Properties

Structure — Filter structure Direct form (default) | Direct form symmetric | Direct form antisymmetric | Direct form transposed | Lattice MA

NumeratorSource — Source of filter coefficients Property (default) | Input port

Dependencies

ReflectionCoefficientsSource — Source of filter coefficients Property (default) | Input port

Dependencies

Numerator — Numerator coefficients [0.5 0.5] (default) | row vector

Dependencies

ReflectionCoefficients — Reflection coefficients of lattice filter structure [0.5 0.5] (default) | row vector

Dependencies

InitialConditions — Initial conditions for the FIR filter 0 (default) | scalar | vector | matrix

Fixed-Point Properties

FullPrecisionOverride — Full precision override for fixed-point arithmetic true (default) | false

RoundingMethod — Rounding method for fixed-point operations Floor (default) | Ceiling | Convergent | Nearest | Round | Simplest | Zero

Dependencies

OverflowAction — Overflow action for fixed-point operations Wrap (default) | Saturate

Dependencies

CoefficientsDataType — Coefficients word and fraction lengths Same word length as input (default) | Custom

Dependencies

CustomCoefficientsDataType — Custom coefficients word and fraction lengths numerictype(true,16,15) (default) | numerictype

Dependencies

ReflectionCoefficientsDataType — Reflection coefficients word and fraction lengths Same word length as input (default) | Custom

Dependencies

CustomReflectionCoefficientsDataType — Custom reflection coefficients word and fraction lengths numerictype(true,16,15) (default) | numerictype

Dependencies

ProductDataType — Product word and fraction lengths Full precision (default) | Same as input | Custom

CustomProductDataType — Custom product word and fraction lengths numerictype(true,32,30) (default) | numerictype

Dependencies

AccumulatorDataType — Accumulator word and fraction lengths Full precision (default) | Same as input | Same as product | Custom

CustomAccumulatorDataType — Custom accumulator word and fraction lengths numerictype(true,32,30) (default) | numerictype

Dependencies

StateDataType — State word and fraction lengths Same as accumulator (default) | Same as input | Custom

Dependencies

CustomStateDataType — Custom state word and fraction lengths numerictype(true,16,15) (default) | numerictype

Dependencies

OutputDataType — Output word and fraction lengths Same as accumulator (default) | Same as input | Custom

CustomOutputDataType — Custom output word and fraction lengths numerictype(true,16,15) (default) | numerictype

Dependencies

Usage

Syntax

Description

Input Arguments

x — Data input vector | matrix

coeff — Filter coefficients row vector

Output Arguments

y — Filtered output vector | matrix

Object Functions

Specific to dsp.FIRFilter

Common to All System Objects

Examples

Lowpass Filter a Sinusoid Signal Using FIRFilter object

Design and Implement Lowpass FIR Filter with Tunable Cutoff Frequency

Design and Implement Lowpass FIR Filter Object

Design and Implement Equiripple FIR Halfband Filter

Design Lowpass FIR Filter Using designfilt

Algorithms

Extended Capabilities

C/C++ Code Generation Generate C and C++ code using MATLAB® Coder™.

HDL Code Generation Generate VHDL, Verilog and SystemVerilog code for FPGA and ASIC designs using HDL Coder™.

Version History

R2023b: The designfilt function and the Design Filter Live Editor task support dsp.FIRFilter object

See Also

Functions

Objects

Blocks

Topics

`Structure` — Filter structure
`Direct form` (default) | `Direct form symmetric` | `Direct form antisymmetric` | `Direct form transposed` | `Lattice MA`

`NumeratorSource` — Source of filter coefficients
`Property` (default) | `Input port`

`ReflectionCoefficientsSource` — Source of filter coefficients
`Property` (default) | `Input port`

`Numerator` — Numerator coefficients
`[0.5 0.5]` (default) | row vector

`ReflectionCoefficients` — Reflection coefficients of lattice filter structure
`[0.5 0.5]` (default) | row vector

`InitialConditions` — Initial conditions for the FIR filter
`0` (default) | scalar | vector | matrix

`FullPrecisionOverride` — Full precision override for fixed-point arithmetic
`true` (default) | `false`

`RoundingMethod` — Rounding method for fixed-point operations
`Floor` (default) | `Ceiling` | `Convergent` | `Nearest` | `Round` | `Simplest` | `Zero`

`OverflowAction` — Overflow action for fixed-point operations
`Wrap` (default) | `Saturate`

`CoefficientsDataType` — Coefficients word and fraction lengths
`Same word length as input` (default) | `Custom`

`CustomCoefficientsDataType` — Custom coefficients word and fraction lengths
`numerictype(true,16,15)` (default) | numerictype

`ReflectionCoefficientsDataType` — Reflection coefficients word and fraction lengths
`Same word length as input` (default) | `Custom`

`CustomReflectionCoefficientsDataType` — Custom reflection coefficients word and fraction lengths
`numerictype(true,16,15)` (default) | numerictype

`ProductDataType` — Product word and fraction lengths
`Full precision` (default) | `Same as input` | `Custom`

`CustomProductDataType` — Custom product word and fraction lengths
`numerictype(true,32,30)` (default) | numerictype

`AccumulatorDataType` — Accumulator word and fraction lengths
`Full precision` (default) | `Same as input` | `Same as product` | `Custom`

`CustomAccumulatorDataType` — Custom accumulator word and fraction lengths
`numerictype(true,32,30)` (default) | numerictype

`StateDataType` — State word and fraction lengths
`Same as accumulator` (default) | `Same as input` | `Custom`

`CustomStateDataType` — Custom state word and fraction lengths
`numerictype(true,16,15)` (default) | numerictype

`OutputDataType` — Output word and fraction lengths
`Same as accumulator` (default) | `Same as input` | `Custom`

`CustomOutputDataType` — Custom output word and fraction lengths
`numerictype(true,16,15)` (default) | `numerictype`

`x` — Data input
vector | matrix

`coeff` — Filter coefficients
row vector

`y` — Filtered output
vector | matrix

Specific to `dsp.FIRFilter`

Design Lowpass FIR Filter Using `designfilt`

C/C++ Code Generation
Generate C and C++ code using MATLAB® Coder™.

HDL Code Generation
Generate VHDL, Verilog and SystemVerilog code for FPGA and ASIC designs using HDL Coder™.

R2023b: The `designfilt` function and the Design Filter Live Editor task support `dsp.FIRFilter` object