outputDelay

Determine output delay of single-rate or multirate filter

Since R2022a

collapse all in page

Syntax

D = outputDelay(sysobj)

[D,FsOut] = outputDelay(sysobj)

[D,FsOut,B] = outputDelay(sysobj)

[___] = outputDelay(sysobj,Name=Value)

Description

D = outputDelay(sysobj) returns the system output delay of the single-rate or multirate filter object. A multirate filter is any cascade combining upsampling, downsampling, and convolution filters (FIR or IIR). Single-rate filters are special cases of multirate filters with a rate conversion factor of 1. The delay D results from the group delay of the convolution stages within the filter.

Use this syntax when sysobj is a linear-phase single-rate filter. To determine if a filter object has linear phase, use the islinphase function.

example

[D,FsOut] = outputDelay(sysobj) also returns the output sample rate. Use this syntax when sysobj is a linear-phase multirate filter.

example

[D,FsOut,B] = outputDelay(sysobj) also returns the input frequency band B over which the delay value is within the default tolerance of 5% (in input sample units) of D. That is, $| D (f) - D | \leq 0.05 / F s I n$ , where f is a frequency in the band B.

Use this syntax when sysobj has filter stages that have a nonlinear phase.

example

[___] = outputDelay(sysobj,Name=Value) specifies options using one or more name-value arguments in addition to the input arguments in previous syntaxes. For example, outputDelay(sysobj, Tol=0.01) estimates the band of input frequencies over which the delay value is within the tolerance of 1%.

Use this syntax to specify FsIn, Fc, Tol, and FFTLength.

example

Examples

collapse all

Compute Output Delay of Filter Cascade

Open Live Script

Compute the output delay of a cascade of dsp.FIRRateConverter objects. Use this delay value to plot the input and resampled signals on the same plot in a time scope.

Resample Input Signal

First, let us inspect the delay and scaling that occurs in filtering. To do that, create a sinusoidal input signal. Initialize a cascade of dsp.FIRRateConverter objects to resample the input signal.

n = (0:7*17-1)';
u = cos(6*pi*n/147);

src = cascade(dsp.FIRRateConverter(13,17), dsp.FIRRateConverter(18,7))

src = 
  dsp.FilterCascade with properties:

         Stage1: [1x1 dsp.FIRRateConverter]
         Stage2: [1x1 dsp.FIRRateConverter]
    CloneStages: true

Resample the input signal by passing the signal through the cascade of dsp.FIRRateConverter objects.

y = src(u);

Plot the Input and Output Signals

Initialize a time scope using the timescope object to visualize the input and the resampled signals.

tsnosync = timescope(NumInputPorts=2,...
            ChannelNames={'Input','Output'});

Plot the input and the resampled signals on the same plot in the time scope. You can see that the two signals are out of sync with respect to each other by a certain amount of delay and stretch over a different time scale

tsnosync(u,y);

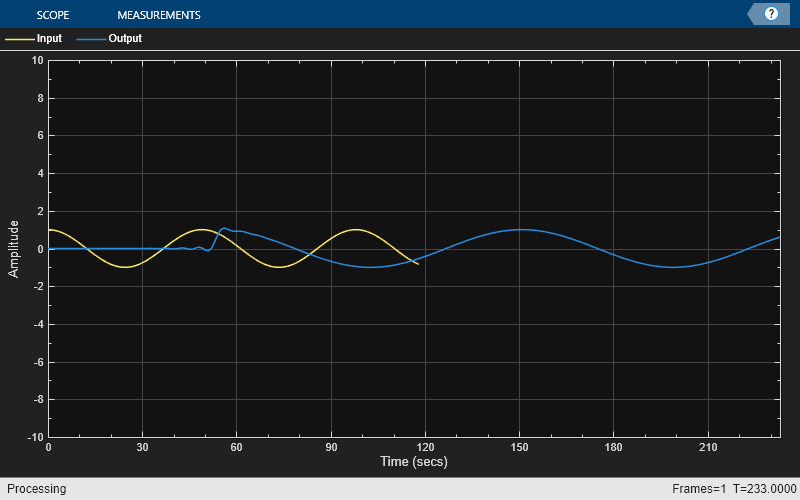
Using outputDelay to Synchronize Signals

To plot the input and resampled signals on the same plot, you need to account for the output delay of the filter. To compute the output delay, use the outputDelay function. The value of this delay depends on the filter structure and order, the rate conversion factor, and the signal input to the filter. In addition to the output delay, the rate conversion operation of the filter introduces scaling on the time domain. You must account for the output delay and the scaling.

Use the outputDelay function to compute the delay and the output sample rate introduced by the multirate filter. You can optionally specify the input sample rate to the function. Apply the delay value to the output signal through the TimeDisplayOffset property of the time scope.

To account for the scaling, specify the input and output sample rates through the SampleRate property of the time scope. The inverse of the input and output sample rates vector determines the x-axis (time axis) spacing between points in the input signal and the output signal, respectively.

Initialize the time scope to use the updated TimeDisplayOffet and SampleRate properties. Visualize the input and the resampled signals on the time scope. With the delay and scaling accounted for, you can see that signals are synchronized and have no delay with respect to each other.

FsIn = 44.1e2; 
[D,FsOut] = outputDelay(src,FsIn=FsIn);

tssync = timescope(NumInputPorts=2,...
            SampleRate=[FsIn FsOut], ...
            TimeDisplayOffset=[0, -D],...
            ChannelNames={'Input','Output'});
tssync(u,y);

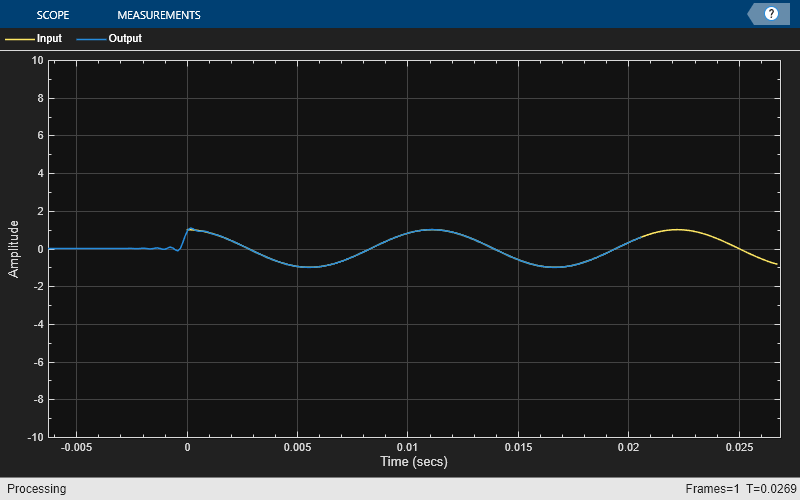
Compute Output Delay for Farrow Rate Converter

Open Live Script

Compute the output delay for a farrow rate converter, and use this delay value to plot the input sinusoidal signal and the rate converted signal on the same plot.

Create an input sinusoidal signal using the sin function. Initialize the dsp.FarrowRateConverter object to model the farrow rate converter.

u = sin(6*pi*(1:50)'/200);
FsIn = 48000;
frc = dsp.FarrowRateConverter(FsIn, 44100);

Compute the output delay of the rate converter using the outputDelay function.

[D, FsOut] = outputDelay(frc)

D = 
4.1667e-05

FsOut = 
44100

Resample the input using the farrow rate converter. Visualize the input signal and the resampled signal on the time scope. To account for the time delay and the scaling, set the TimeDisplayOffset and SampleRate properties of the time scope to [ $0 - D$ ] and [FsIn FsOut], respectively.

y = frc(u);
ts = timescope(NumInputPorts = 2, SampleRate = [FsIn FsOut], ...
    TimeDisplayOffset = [0, -D],...
    ChannelNames = {'Input','Output'}, ...
    TimeSpan = length(y)*1.1/FsIn, ...
    PlotType = 'stem');
ts(u, y);

Calculate Frequency Band for Nonlinear Phase Filters

Open Live Script

Nonlinear phase filters have a group delay that depends on the input frequency. Due to the nonlinear phase nature, such filters distort input signals. Therefore, the output of these filters cannot be obtained by shifting and scaling the input on the time domain. To use the outputDelay function to compute the output delay of such filters, the filters must have a relatively constant group delay over the input signal band.

Start by calculating the frequency band of two nonlinear fractional delay FIR filters with partially flat group delay. One filter has a higher bandwidth compared to the other filter. Note the effect of the higher bandwidth on the output delay and the input frequency band over which the function computes the delay.

Then, consider a multirate filter cascade that has a highly nonlinear group delay response over a given band but has a relatively flat group delay over other frequency bands. Increase the tolerance value that you specify to the outputDelay function and see the effect on the input frequency band that the function returns.

Fractional Delay FIR Filter with Nonlinear Phase and Partially Flat Group Delay

Since the fractional delay FIR filter has a nonlinear phase response, specify a center frequency around which the outputDelay function should compute the delay. When you specify the center frequency, the function returns an interval of frequencies (as the third output argument) over which the delay value is within the specified tolerance.

Design a fractional delay filter using the designFracDelayFIR function. Specify the filter to have a fractional delay of 1.25e-3 seconds and a passband coverage of 50%.

FsIn = 20;
Fc = 1;
FD = 1.25e-3;

nlPhaseFilterObj1 = dsp.FIRFilter(designFracDelayFIR(FD*FsIn, 0.5));

Using the outputDelay function, calculate the output delay around the center frequency of 1 Hz. Specify the input sample rate to 20 Hz and the tolerance to 0.01 (1%). In addition to the output delay, the function returns the input band over which the deviation in delay is up to 1% of D1.

[D1,~,B1] = outputDelay(nlPhaseFilterObj1,FsIn=FsIn,Fc=Fc,Tol=0.01)

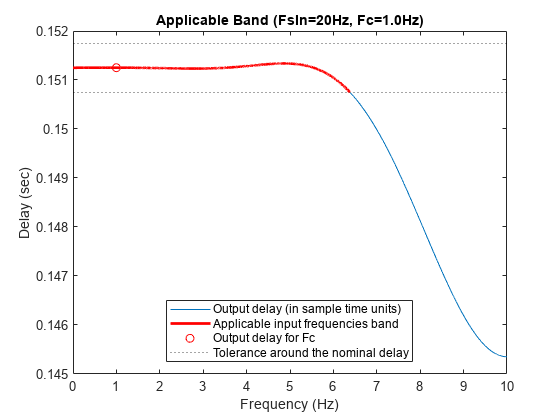
D1 = 
0.1513

B1 = 1×2

   -6.3794    6.3794

Use the grpdelay function to compute the group delay G of the filter and the frequencies W (in Hz) at which the group delay is evaluated. Specify the FFT length to 8192, and the sample rate to be the same as the input sample rate.

Plot the overall filter group delay. On the same figure, plot the input frequency band and the output delay value at the center frequency. The input frequency band indeed contains the center frequency.

[G1,W1] = nlPhaseFilterObj1.grpdelay(8192, FsIn); % Use 8192 FFT points to calculate the group delay
I1 = W1>=B1(1) & W1<=B1(2);  % Mask applicable frequencies

plot(W1,G1/FsIn);
hold on
plot(W1(I1), G1(I1)/FsIn, 'r', LineWidth=2);
plot(Fc, D1, 'ro');
yline(D1+0.01/FsIn*[-1 1],'k:');

title(sprintf('Applicable Band (FsIn=%iHz, Fc=%1.1fHz)',FsIn,Fc))
legend('Output delay (in sample time units)',...
    'Applicable input frequencies band',...
    'Output delay for Fc',...
    'Tolerance around the nominal delay', Location='best')
ylabel('Delay (sec)')
xlabel('Frequency (Hz)')
hold off

Comparing with Higher Bandwidth Design

Compare the previous design with a higher bandwidth fractional delay design. For more information on the bandwidth of a fractional-delay FIR filter, see designFracDelayFIR.

Design a fractional-delay FIR filter with the same fractional delay (1.25e-3 seconds) as the previous design but with a 70% bandwidth coverage.

nlPhaseFilterObj2 = dsp.FIRFilter(designFracDelayFIR(FD*FsIn, 0.7));

Measure the output delay of this alternative design. The output delay D2 is larger due to the longer FIR length, but the input band is also larger, allowing signals up to 7.2Hz (compared with only 6.4 Hz in the previous design).

[D2,~,B2] = outputDelay(nlPhaseFilterObj2,FsIn=FsIn,Fc=Fc,Tol=0.01)

D2 = 
0.2512

B2 = 1×2

   -7.2217    7.2217

[G2,W2] = nlPhaseFilterObj2.grpdelay(8192, FsIn);

Plot the group delay response of the alternative design against the design with a 50% coverage.

I2 = W2>=B2(1) & W2<=B2(2);  % Mask applicable frequencies

plot(W1,G1/FsIn);
hold on
plot(W2,G2/FsIn);
plot(W1(I1), G1(I1)/FsIn, 'r', LineWidth=2);
plot(W2(I2), G2(I2)/FsIn, 'm', LineWidth=2);
title(sprintf('Applicable Band (FsIn=%iHz, Fc=%1.1fHz)',FsIn,Fc))
legend('Output delay (in sample time units) of design 1',...
    'Output delay (in sample time units) of design 2',...
    'Applicable input frequencies band of design 1',...
    'Applicable input frequencies band of design 2', ...
    Location='best')
ylabel('Delay (sec)')
xlabel('Frequency (Hz)')
hold off

Figure contains an axes object. The axes object with title Applicable Band (FsIn=20Hz, Fc=1.0Hz), xlabel Frequency (Hz), ylabel Delay (sec) contains 4 objects of type line. These objects represent Output delay (in sample time units) of design 1, Output delay (in sample time units) of design 2, Applicable input frequencies band of design 1, Applicable input frequencies band of design 2.

Multirate Filter Cascade with Nonlinear Phase

Design a two-stage filter cascade that contains a stable IIR lowpass (which has a nonlinear phase) followed by an FIR decimator with a rate conversion factor of 2.

FsIn = 10;
Fc = 1.5;
LP = dsp.LowpassFilter(FilterType='IIR',SampleRate=FsIn,PassbandFrequency=2.3,StopbandFrequency=2.7);
nlPhaseCascadeObj = cascade(LP, dsp.FIRDecimator(2));

Measure the output delay, output sample rate, and the input frequency band for this cascade using a narrowband input signal with a carrier frequency of 1.5Hz. Set the tolerance to 0.001 samples. The function returns an output sample rate of 5 Hz (which is half the input sample rate of 10 Hz, owing to the half-rate decimator).

[D,FsOut,B] = outputDelay(nlPhaseCascadeObj, Fc=Fc, Tol=0.001)

D = 
2.9209

FsOut = 
5

B = 1×2

    1.5000    1.5000

The band the function returns is a trivial band. That is, it contains a single point (the left and right boundaries are the same). This means that a tolerance value of 0.001 is too small.

To fix that, increase the tolerance to 0.05 seconds (0.5 of the input sample time). While the delay and the output sample rate do not change, the band is now nontrivial, and it contains the center frequency. The band is also relatively narrow due to the highly nonlinear phase nature of the IIR design.

[D1,FsOut1,B1] = outputDelay(nlPhaseCascadeObj, Fc=Fc, Tol=0.5)

D1 = 
2.9209

FsOut1 = 
5

B1 = 1×2

    1.3562    1.5967

Increase the tolerance value to 2. The band now increases even more as you have specified a more lax tolerance.

[D2,FsOut2,B2] = outputDelay(nlPhaseCascadeObj, Fc=Fc, Tol=2)

D2 = 
2.9209

FsOut2 = 
5

B2 = 1×2

    0.4565    1.7786

[G,W] = nlPhaseCascadeObj.grpdelay(8192, FsIn);
I1 = W>=B1(1) & W<=B1(2);  % Mask applicable frequencies
I2 = W>=B2(1) & W<=B2(2);  % Mask applicable frequencies

plot(W,G/FsIn);
hold on
plot(W(I2), G(I2)/FsIn, Color=[0.6 0.1 0.6], LineWidth=2);
plot(W(I1), G(I1)/FsIn, Color=[0 0.7 0.7], LineWidth=4);
plot(Fc, D1, 'ro');
title(sprintf('Applicable Band (FsIn=%iHz, Fc=%1.1fHz)',FsIn,Fc))
legend('Output delay (in sample time units)',...
    'Applicable input frequencies band with Tol=1',...
    'Applicable input frequencies band with Tol=0.5',...
    'Output delay for Fc',...
    Location='best')
ylabel('Delay (sec)')
xlabel('Frequency (Hz)')
hold off

Input Arguments

collapse all

`sysobj` — Input filter
filter System object™

Input filter, specified as one of the following filter System objects:

Name-Value Arguments

Specify optional pairs of arguments as Name1=Value1,...,NameN=ValueN, where Name is the argument name and Value is the corresponding value. Name-value arguments must appear after other arguments, but the order of the pairs does not matter.

Example: FsIn=48000, Fc=-10.3, Tol=0.01, FFTLength=100

`FsIn` — Input sample rate
`1` (default) | positive scalar

Input sample rate of the filter object sysobj, specified as a positive scalar.

If you do not specify FsIn, the function uses the input sample rate specified in the built-in input sample rate property of the filter object if it exists, otherwise the function uses the default rate of 1.

Specify FsIn when you want to override the input sample rate specified in the filter object.

`Fc` — Carrier frequency
`0` (default) | real scalar

Carrier frequency from which the function derives the group delay of the convolution stages, specified as a real scalar. Specify Fc when the filter object sysobj has stages with a nonlinear phase.

For filters with a nonlinear phase (a varying group delay), the delay value D the outputDelay function returns depends on the input frequency. For more details, see Linear and Nonlinear Phase Filters. For an example, see Calculate Frequency Band for Nonlinear Phase Filters.

If you do not specify Fc, the function uses the default center frequency of 0 for most filters except the bandpass and highpass filters. Make sure that the absolute value of the carrier frequency is not larger than the Nyquist frequency. That is, $| f c | \leq F s I n / 2$ , where FsIn is the input sample rate of the filter object.

`Tol` — Tolerance of estimated delay
`0.05` (default) | real scalar

Tolerance of the estimated delay value D, specified as a real scalar. Specify Tol when you want to calculate the input band B.

When you specify a tolerance Tol, the function can estimate a band of input frequencies B for which the delay is close to D up to a given tolerance Tol. That is, $| D (f) - D | \leq T o l / F s I n$ , where f is a frequency in the band given by the B vector.

When you use the following signature, the function uses the default 5% tolerance (in input sample units) of D.

[D,FsOut,B] = outputDelay(sysobj,Fc=fc)

Alternatively, you can specify the tolerance value using the Tol argument.

[D,FsOut,B] = outputDelay(sysobj,Fc=fc,Tol=T)

`FFTLength` — FFT length
`8192` (default) | nonnegative integer

FFT length, specified as a nonnegative integer. Specify FFTLength when you want to calculate the input band B.

This value determines the frequency resolution with which the function estimates the input frequency band B. Higher the FFT length, the higher is the frequency resolution and accuracy of B.

Output Arguments

collapse all

`D` — Output delay
nonnegative scalar

Output or resampling delay of the multirate filter, returned as a nonnegative scalar.

The delay value D is determined by the group delay of the convolution filter stages, and the value depends on the filter structure, filter order, and rate conversion factors. When the filter has a nonlinear phase, the delay value also depends on the input signal.

For filters with a linear phase (that is, a flat group delay), the value of D applies to all inputs. For filters with a nonlinear phase (that is, a varying group delay), the delay value D depends on the input frequencies.

`FsOut` — Output sample rate
positive scalar

Output sample rate of the multirate filter object for the given input sample rate FsIn, returned as a positive scalar.

`B` — Estimated input frequency band
two-element row vector

Estimated input frequency band [f₁ f₂] over which the delay value is within tolerance Tol (in input sample units) of D, returned as a two-element row vector. If you do not specify Tol, the function uses a tolerance value of 0.05 (or 5%).

The frequency band stretches from f₁ counterclockwise to f₂. That is, if f₂ > f₁, then the band is {f₁<f<f₂}. If f₂ < f₁, then the band wraps around the Nyquist frequency, that is the union of {−FsIn/2<f<f₂} and {f₁<f<FsIn/2}. If f₁=f₂, then the band has a single frequency due to the FFT resolution being too coarse. In such cases, increase the value of FFTLength or the tolerance Tol.

Band measurement is available only for systems that can be reduced to a rational rate converter. For a linear phase system, the band B is always full, $B = [- F s I n / 2, F s I n / 2]$ and the delay D is applicable for all input frequencies (flat group delay).

More About

collapse all

Multirate Filters

A multirate filter is any cascade combining upsampling, downsampling, and convolution filters (FIR or IIR).

Most filter System objects in DSP System Toolbox™ are multirate filters. For example, dsp.FIRDecimator(5) is the multirate filter H(z) followed by a downsampler that has a downsampling ratio of 5.

Single-rate filters are special cases of multirate filters with a rate conversion factor of 1. Single-stage filters are special cases of cascades of multirate filters. For example, dsp.LowpassFilter is a single-rate, single-stage filter of the form H(z).

Multirate Filters as Resampling Systems

The outputDelay function assumes that the multirate filter sysobj models a resampling system. The output of the resampling system is a filtered and resampled version of the input, and hence has a different rate compared to the input.

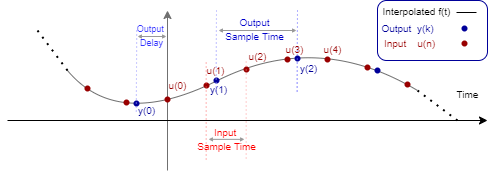
A resampling system interpolates the input u(n) to a continuous domain function f(t) that approximates the input.

$u (n) \approx f (n / F s I n)$

The output is then sampled from f(t) on a different time scale.

$y (k) = f (k / F s O u t - D)$

The values FsIn and FsOut are the input and output sample rates, respectively, and D is the resampling or output delay.

This graph overlays the input and output sequences on the same plot, shows the input and output sample times, and also shows the output delay that the function returns.

Graph of f(t) with input u(n) and output y(k) marked.

For examples that demonstrate the effect of the resampling delay and scaling in multirate filters, see Compute Output Delay of Filter Cascade and Time Delay and Scaling in Multirate DSP Filters.

Output Delay and Group Delay

The output delay and the group delay are related to each other.

The output or resampling delay is the delay of the signal in time units as it goes through a convolution filter (FIR or IIR). For a single-rate filter, the output delay (D) and the group delay ( $τ_{g}$ ) are scaled by the sample rate, $D = τ_{g} / F s I n$ . If the filter has a linear phase, both the output delay and the group delay do not depend on the input frequency. However, if the filter has nonlinear phase, then the group delay and the output delay depend on the input frequency.

This figure shows the impulse response of a symmetric 24-tap FIR filter. You can see that the output delay and the group delay are equivalent quantities in different scales.

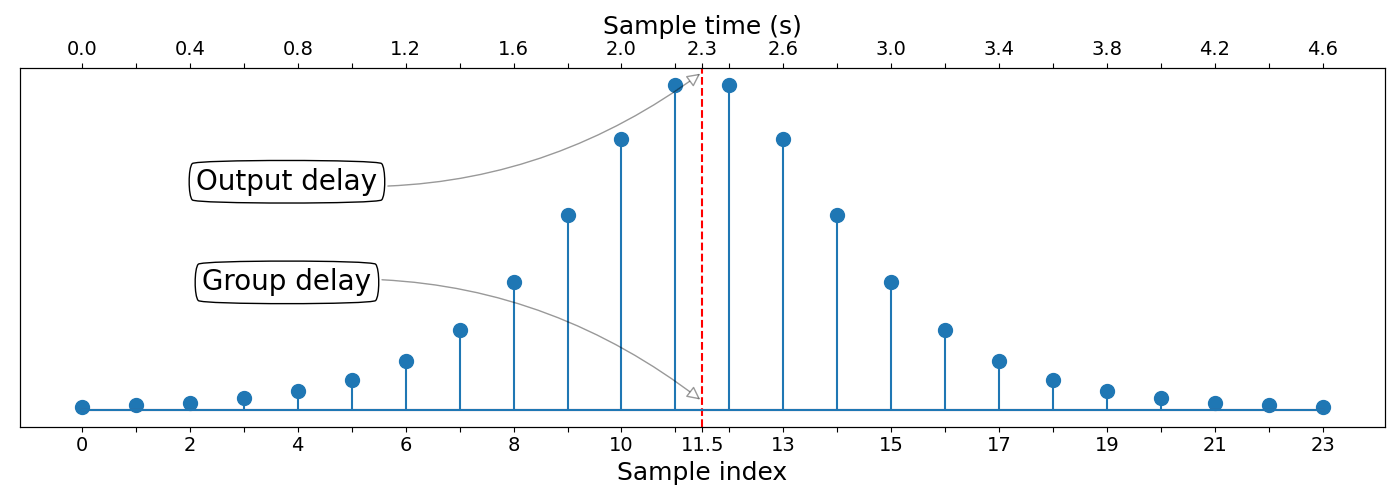
If the filter is a multirate filter, the output delay is the total delay that the filter accumulates on all stages of the cascade. The output sample rate FsOut of each stage becomes the input sample rate FsIn of the subsequent stage. The function scales the delay values accumulated over each stage by the rate conversion factors of the individual stages.

The group delay is defined only for single-rate filters while the output delay is defined for both single-rate and multirate filters.

The group delay refers to the average delay of the convolution filter (FIR or IIR) as a function of frequency. It is computed as the negative first derivative of the phase response of the filter. If the frequency response of a filter is H(e^jω), then the group delay is

$τ_{g} (ω) = - \frac{d θ (ω)}{d ω},$

where θ(ω) is the phase, or argument, of H(e^jω).

If the filter is a linear phase filter, the group delay response is flat. The output delay D does not depend on input frequency. If the filter is a nonlinear phase filter, the group delay response varies with frequency and the delay value D is valid only for bandlimited inputs around a carrier frequency Fc. The function determines the edges of the frequency band B such that the group delay over this frequency region is approximately constant. For more information, see Linear and Nonlinear Phase Filters. For an example, see Time Delay and Scaling in Multirate DSP Filters.

Linear and Nonlinear Phase Filters

Depending on the group delay of the filter stages (whether flat or varies with frequency), the outputDelay function can operate in two modes.

If all the filter stages have a linear phase (flat group delay), then the outputDelay function operates in the full band mode. If the individual filter stages have a nonlinear phase but can be reordered through noble identity operations such that the equivalent stage has a linear phase, then the outputDelay function operates in the full band mode and you do not need to specify the carrier frequency Fc.

For an example of nonlinear filter stages having a linear phase equivalent, see A Nonlinear Phase Multirate Filter with Linear Phase Equivalent.

If one or more stages have a nonlinear phase, and the filter does not have a linear phase equivalent, then the outputDelay function operates in the bandlimited mode. In the bandlimited mode, the function requires you to specify the input center frequency Fc in order to compute the delay.

Full-Band Mode in Linear Phase Filters

In the full band mode, the delay value D applies to all inputs. All symmetric filter designs work in this mode.

The outputDelay function uses the group delay of the filter stages to calculate the overall output delay. When the filters have a linear phase, the group delay of the filter does not vary with frequency. The band B is always full (flat group delay).

For symmetric filters, the output delay (D) can be thought of as the center of mass of the impulse response (h[k]), which can be obtained by the weighted sum:

$\begin{array}{l} D = \frac{1}{F s I n} \cdot τ_{g}, \\ D = \frac{1}{F s I n} \cdot \frac{\sum_{k = 0}^{L - 1} k \cdot h [k]}{\sum_{j = 0}^{L - 1} h [j]} \end{array}$

where $τ_{g}$ is the group delay of the filter, and L is the length of the filter.

The function obtains the output delay by scaling the center of mass with the sample time. For an example, see Time Delay and Scaling in Multirate DSP Filters.

This center-of-mass delay formulation can be generalized for asymmetric filters, where it takes the form of group delay. Symmetric and anti-symmetric filters have a linear phase response, hence their group delay response is constant and does not depend on frequency. Filters with a varying group delay (nonlinear phase filters) can exhibit distortion on the time domain.

Bandlimited Mode for Nonlinear Phase Filters

In the bandlimited mode, the outputDelay function calculates the delay D for the input frequency Fc. The function uses this mode with filters that have nonlinear phase stages. Many causal and stable rational IIR filters have a nonlinear phase, and therefore have a varying group delay. Generally, those filters distort input signals, which breaks the resampling model described in Multirate Filters. In such cases, the resampling model and the delay value D are valid only for bandlimited inputs around Fc. The function determines the width of the frequency band B such that the group delay over this frequency region is approximately constant. Use the grpdelay function to inspect the flatness of the group delay of the filter stages.

Assume that the input is a narrowband signal centered around some carrier frequency ω_c = 2πFc. The resampling model is slightly different in this case, where the input is

$u (n) \approx f (n / F s I n) \cdot \cos (ω_{c} n),$

and the output is given by

$y (k) \approx f (k / F s O u t - D) \cdot \cos (ω_{c} (k / F s O u t - D_{p})) .$

The baseband is delayed by output delay D, which is calculated using the group delay specific to the input frequency. The carrier, however, experiences a different delay, D_p, which is obtained by the phase delay of the filter rather than its group delay.

You can specify the input carrier frequency through the input argument Fc. The outputDelay function can also calculate the interval of input frequencies B that the value of D is applicable up to a certain tolerance. This band is returned as the third return value of the function (with the second one being the output sample rate FsOut). The tolerance (in sample time units) can be specified using the Tol argument.

To determine if a filter object is linear, use the islinphase function.

A Nonlinear Phase Multirate Filter with Linear Phase Equivalent

Consider the multirate filter cascade below with nonlinear phase filter stages Q(z) and R(z).

The noble identify for decimation is given by:

Apply the noble identity for decimation on R(z). The product Q(z)R(z²) is a linear phase system.

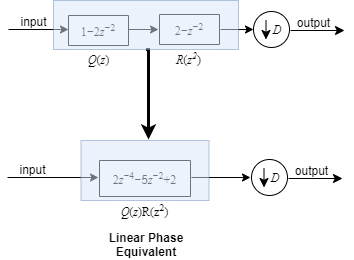
Even though the individual filter stages have a nonlinear phase, the combined equivalent filter after applying the noble identify has a linear phase. The outputDelay function treats this filter as a linear phase filter.

All combinations of nonlinear phase stages cannot be reordered to form linear phase equivalents. The function treats such filters as nonlinear filters and operates in the bandlimited mode.

Version History

Introduced in R2022a

expand all

R2024b: Support for `dsp.VariableFIRDecimator` and `dsp.VariableFIRInterpolator` Objects

Starting in R2024b, the outputDelay function supports the dsp.VariableFIRDecimator and dsp.VariableFIRInterpolator objects.

R2024b: `dsp.BiquadFilter` object warns

The dsp.BiquadFilter object issues a warning and will be removed in a future release. Use the dsp.SOSFilter object instead. For more information on how to replace your existing code, see the Compatibility Considerations section in the dsp.BiquadFilter reference page.

R2024b: Support for `dsp.DCBlocker` object

Starting in R2024b, this function supports the dsp.DCBlocker object.

R2023b: Support for `dsp.ParallelFilter` and `dsp.Delay` Objects

Starting in R2023b, the outputDelay analysis function supports the dsp.ParallelFilter and the dsp.Delay objects.

R2023b: `dsp.BiquadFilter` object will be removed

The dsp.BiquadFilter object will be removed in a future release. Use the dsp.SOSFilter object instead.

outputDelay

Syntax

Description

Examples

Compute Output Delay of Filter Cascade

Compute Output Delay for Farrow Rate Converter

Calculate Frequency Band for Nonlinear Phase Filters

Input Arguments

`sysobj` — Input filter
filter System object™

Name-Value Arguments

`FsIn` — Input sample rate
`1` (default) | positive scalar

`Fc` — Carrier frequency
`0` (default) | real scalar

`Tol` — Tolerance of estimated delay
`0.05` (default) | real scalar

`FFTLength` — FFT length
`8192` (default) | nonnegative integer

Output Arguments

`D` — Output delay
nonnegative scalar

`FsOut` — Output sample rate
positive scalar

`B` — Estimated input frequency band
two-element row vector

More About

Multirate Filters

Output Delay and Group Delay

Linear and Nonlinear Phase Filters

A Nonlinear Phase Multirate Filter with Linear Phase Equivalent

Version History

R2024b: Support for `dsp.VariableFIRDecimator` and `dsp.VariableFIRInterpolator` Objects

R2024b: `dsp.BiquadFilter` object warns

R2024b: Support for `dsp.DCBlocker` object

R2023b: Support for `dsp.ParallelFilter` and `dsp.Delay` Objects

R2023b: `dsp.BiquadFilter` object will be removed

See Also

Topics

outputDelay

Syntax

Description

Examples

Compute Output Delay of Filter Cascade

Compute Output Delay for Farrow Rate Converter

Calculate Frequency Band for Nonlinear Phase Filters

Input Arguments

sysobj — Input filter filter System object™

Name-Value Arguments

FsIn — Input sample rate 1 (default) | positive scalar

Fc — Carrier frequency 0 (default) | real scalar

Tol — Tolerance of estimated delay 0.05 (default) | real scalar

FFTLength — FFT length 8192 (default) | nonnegative integer

Output Arguments

D — Output delay nonnegative scalar

FsOut — Output sample rate positive scalar

B — Estimated input frequency band two-element row vector

More About

Multirate Filters

Output Delay and Group Delay

Linear and Nonlinear Phase Filters

A Nonlinear Phase Multirate Filter with Linear Phase Equivalent

Version History

R2024b: Support for dsp.VariableFIRDecimator and dsp.VariableFIRInterpolator Objects

R2024b: dsp.BiquadFilter object warns

R2024b: Support for dsp.DCBlocker object

R2023b: Support for dsp.ParallelFilter and dsp.Delay Objects

R2023b: dsp.BiquadFilter object will be removed

See Also

Topics

`sysobj` — Input filter
filter System object™

`FsIn` — Input sample rate
`1` (default) | positive scalar

`Fc` — Carrier frequency
`0` (default) | real scalar

`Tol` — Tolerance of estimated delay
`0.05` (default) | real scalar

`FFTLength` — FFT length
`8192` (default) | nonnegative integer

`D` — Output delay
nonnegative scalar

`FsOut` — Output sample rate
positive scalar

`B` — Estimated input frequency band
two-element row vector

R2024b: Support for `dsp.VariableFIRDecimator` and `dsp.VariableFIRInterpolator` Objects

R2024b: `dsp.BiquadFilter` object warns

R2024b: Support for `dsp.DCBlocker` object

R2023b: Support for `dsp.ParallelFilter` and `dsp.Delay` Objects

R2023b: `dsp.BiquadFilter` object will be removed