dsp.IIRHalfbandDecimator

Decimate by factor of two using polyphase IIR

Description

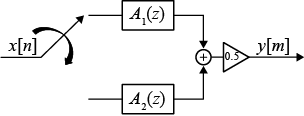
The dsp.IIRHalfbandDecimator System object™ performs efficient polyphase decimation of the input signal by a factor of two. To design the halfband filter, you can specify the object to use an elliptic design or a quasi-linear phase design. The object uses these design methods to compute the filter coefficients. To filter the inputs, the object uses a polyphase structure. The allpass filters in the polyphase structure are in a minimum multiplier form.

Elliptic design introduces nonlinear phase and creates the filter using fewer coefficients than quasi linear design. Quasi-linear phase design overcomes phase nonlinearity at the cost of additional coefficients.

Alternatively, instead of designing the halfband filter using a design method, you can specify the filter coefficients directly. When you choose this option, the allpass filters in the two branches of the polyphase implementation can be in a minimum multiplier form or in a wave digital form.

You can also use the dsp.IIRHalfbandDecimator object to implement the analysis portion of a two-band filter bank to filter a signal into lowpass and highpass subbands.

To filter and downsample your data:

Create the dsp.IIRHalfbandDecimator object and set its properties.
Call the object with arguments, as if it were a function.

To learn more about how System objects work, see What Are System Objects?

Creation

Syntax

iirhalfbanddecim = dsp.IIRHalfbandDecimator

iirhalfbanddecim = dsp.IIRHalfbandDecimator(Name=Value)

Description

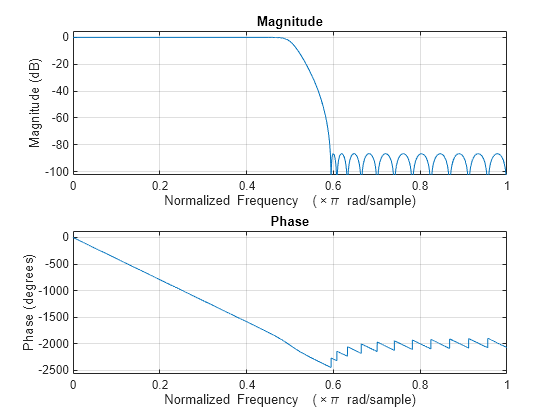
iirhalfbanddecim = dsp.IIRHalfbandDecimator returns a halfband decimator, iirhalfbanddecim, with the default settings. Under the default settings, the System object filters and downsamples the input data with a halfband frequency of 22050 Hz, a transition width of 4100 Hz, and a stopband attenuation of 80 dB.

iirhalfbanddecim = dsp.IIRHalfbandDecimator(Name=Value) returns an IIR halfband decimator, with additional properties specified by one or more Name-Value pair arguments.

Example: iirhalfbanddecim = dsp.IIRHalfbandDecimator(Specification="Filter order and stopband attenuation") creates an IIR halfband decimator object with filter order set to 9 and stopband attenuation set to 80 dB.

example

Properties

expand all

Unless otherwise indicated, properties are nontunable, which means you cannot change their values after calling the object. Objects lock when you call them, and the release function unlocks them.

If a property is tunable, you can change its value at any time.

For more information on changing property values, see System Design in MATLAB Using System Objects.

Main Properties

`Specification` — Filter design parameters
`"Transition width and stopband attenuation"` (default) | `"Filter order and stopband attenuation"` | `"Filter order and transition width"` | `"Coefficients"`

Filter design parameters, specified as a character vector. When you set Specification to one of the filter design options, you can specify the filter design parameters using the corresponding FilterOrder, StopbandAttenuation, and TransitionWidth properties. Also, you can specify the design method using DesignMethod. When you set Specification to "Coefficients", you can specify the coefficients directly.

`FilterOrder` — Order of the IIR halfband filter
9 (default) | positive scalar integer

Order of the IIR halfband filter, specified as a positive scalar integer. If you set DesignMethod to "Elliptic", then FilterOrder must be an odd integer greater than one. If you set DesignMethod to "Quasi-linear phase", then FilterOrder must be a multiple of four.

Dependencies

To enable this property, set Specification to "Filter order and stopband attenuation" or "Filter order and transition width".

`StopbandAttenuation` — Minimum attenuation needed in stopband
80 (default) | positive real scalar

Minimum attenuation needed in the stopband of the IIR halfband filter, specified as a positive real scalar. Units are in dB.

Dependencies

To enable this property, set Specification to "Filter order and stopband attenuation" or "Transition width and stopband attenuation".

Data Types: single | double

`TransitionWidth` — Transition width
4100 (default) | positive real scalar

Transition width of the IIR halfband filter, specified as a positive real scalar or in normalized frequency units (since R2023b).

If you set the NormalizedFrequency property to:

false –– The value of the transition width is in Hz and must be less than half the SampleRate property value.
true –– The value of the transition width is in normalized frequency units. The value must be a positive scalar less than 1.0.
When you set the NormalizedFrequency property to true while creating the object and you do not set the transition width, the object sets the default transition width to normalized frequency units using the default sample rate of 44100 Hz.
When you set the NormalizedFrequency property to true after you create the object, you must specify the transition width in normalized units before you run the object algorithm. To specify the normalized frequency value, set NormalizedFrequency to true and manually convert the frequency value in Hz to the normalized value using the input sample rate in Hz. For example, if the input sample rate Fs is 44100 Hz, the corresponding transition width value in normalized units is TW_Hz/(Fs/2).
```
iirhalfbanddecim = dsp.IIRHalfbandDecimator;
iirhalfbanddecim.NormalizedFrequency = true;
iirhalfbanddecim.TransitionWidth = 4100/(44100/2)
```

(since R2023b)

Dependencies

To enable this property, set Specification to "Transition width and stopband attenuation" or "Filter order and transition width".

Data Types: single | double

`DesignMethod` — Design method
`"Elliptic"` (default) | `"Quasi-linear phase"`

Design method for the IIR halfband filter, specified as "Elliptic" or "Quasi-linear phase". When you set this property to "Quasi-linear phase", the first branch of the polyphase structure is a pure delay, which results in an approximately linear phase response.

Dependencies

To enable this property, set Specification to any accepted value except "Coefficients".

`NormalizedFrequency` — Flag to set frequencies in normalized units
`false` (default) | `true`

Since R2023b

Flag to set frequencies in normalized units, specified as one of these values:

true –– The transition width must be in the normalized frequency units and less than 1.0.
When you set the NormalizedFrequency property to true while creating the object and you do not set the transition width, the object sets the default transition width to normalized frequency units using the default sample rate of 44100 Hz.
When you set the NormalizedFrequency property to true after you create the object, you must specify the transition width in normalized units before you run the object algorithm. To specify the normalized frequency value, set NormalizedFrequency to true and manually convert the frequency value in Hz to the normalized value using the input sample rate in Hz. For example, if the input sample rate Fs is 44100 Hz, the corresponding transition width value in normalized units is TW_Hz/(Fs/2).
```
iirhalfbanddecim = dsp.IIRHalfbandDecimator;
iirhalfbanddecim.NormalizedFrequency = true;
iirhalfbanddecim.TransitionWidth = 4100/(44100/2)
```
false –– The transition width is in Hz. You can specify the input sample rate through the SampleRate property.

Dependency

To enable this property, set Specification to any accepted value except "Coefficients".

Data Types: logical

`SampleRate` — Input sample rate
44100 (default) | positive real scalar

Input sample rate in Hz, specified as a positive real scalar.

Dependency

To enable this property, set:

Specification to any accepted value except "Coefficients".
NormalizedFrequency to false. (since R2023b)

Data Types: single | double

`Structure` — Internal allpass filter implementation structure
`"Minimum multiplier"` (default) | `"Wave Digital Filter"`

Internal allpass filter implementation structure, specified as "Minimum multiplier" or "Wave Digital Filter".

This property is not tunable.

Dependencies

To enable this property, set Specification to "Coefficients". Each structure uses a different coefficients set, independently stored in the corresponding object property.

`AllpassCoefficients1` — Allpass polynomial filter coefficients of first branch
`[0.1284563; 0.7906755]` (default) | `[0.1284563 0.1534; 0.7906755 0.6745]`

Allpass polynomial filter coefficients of the first branch, specified as an N-by-1 or N-by-2 matrix. N is the number of first-order or second-order allpass sections.

Tunable: Yes

Dependencies

To enable this property, set Specification to "Coefficients" and Structure to "Minimum multiplier".

`AllpassCoefficients2` — Allpass polynomial filter coefficients of second branch
`[0.4295667]` (default) | `[0.7906755 0.1534]`

Allpass polynomial filter coefficients of the second branch, specified as an N-by-1 or N-by-2 matrix. N is the number of first-order or second-order allpass sections.

Tunable: Yes

Dependencies

To enable this property, set Specification to "Coefficients" and Structure to "Minimum multiplier".

`WDFCoefficients1` — Allpass filter coefficients of first branch in Wave Digital Filter form
`[0.1284563; 0.7906755]` (default) | `[0.1284563 0.1534; 0.7906755 0.6745]`

Allpass filter coefficients of the first branch in Wave Digital Filter form, specified as an N-by-1 or N-by-2 matrix. N is the number of first-order or second-order allpass sections. Each element must have an absolute value less than or equal to 1.

This property is not tunable.

Dependencies

To enable this property, set Specification to "Coefficients" and Structure to "Wave Digital Filter".

`WDFCoefficients2` — Allpass filter coefficients of second branch in Wave Digital Filter form
`[0.4295667]` (default) | `[0.7906755 0.1534]`

Allpass filter coefficients of the second branch in Wave Digital Filter form, specified as the comma-separated pair consisting of 'WDFCoefficients2' and a N-by-1 or N-by-2 matrix. N is the number of first-order or second-order allpass sections. Each element must have an absolute value less than or equal to 1.

This property is not tunable.

Dependencies

To enable this property, set Specification to "Coefficients" and Structure to "Wave Digital Filter".

`HasPureDelayBranch` — Make first branch a pure delay
`false` (default) | `true`

Flag to make the first allpass branch a delay, specified as a logical scalar. When this property is true, the first branch is treated as a pure delay and the properties AllpassCoefficients1 and WDFCoefficients1 do not apply.

This property is not tunable.

Dependencies

To enable this property, set Specification to "Coefficients".

`Delay` — Length of delay
`1` (default) | finite positive scalar

Length of the first branch delay, specified as a finite positive scalar. The value of this property specifies the number of samples by which you can delay the input to the first branch.

This property is not tunable.

Dependencies

To enable this property, set Specification to "Coefficients" and HasPureDelayBranch to 1.

Data Types: single | double

`HasTrailingFirstOrderSection` — Treat the last section of the second branch as first order
`false` (default) | `true`

Option to treat the last section of the second branch as first order, specified as a logical scalar. When this property is 1 and the coefficients of the second branch are in an N-by-2 matrix, the object ignores the second element of the last row of the matrix. The last section of the second branch then becomes a first-order section. When this property is set to 0, the last section of the second branch is a second-order section. When the coefficients of the second branch are in an N-by-1 matrix, this property is ignored.

This property is not tunable.

Dependencies

To enable this property, set Specification to "Coefficients".

Code Generation Properties

`AllowArbitraryInputLength` — Allow arbitrary input length in generated code
`false` (default) | `true`

Allow arbitrary frame length for fixed-size input signals in the generated code, specified as true or false. When you specify:

true –– The input frame length does not have to be a multiple of the decimation factor 2. The output of the object in the generated code is a variable-size array.
false –– The input frame length must be a multiple of the decimation factor 2.

When you specify variable-size signals, the input frame length can be arbitrary and the object ignores this property in the generated code. When you run this object in MATLAB^®, the object supports arbitrary input frame lengths for fixed-size and variable-size signals and this property does not affect the object behavior.

Data Types: logical

Usage

Syntax

ylow = iirhalfbanddecim(x)

[ylow,yhigh] = iirhalfbanddecim(x)

Description

ylow = iirhalfbanddecim(x) filters the input signal, x, using the IIR halfband filter, iirhalfbanddecim, and downsamples the output by a factor of 2.

example

[ylow,yhigh] = iirhalfbanddecim(x) computes the ylow and yhigh, of the analysis filter bank, iirhalfbanddecim for input x. A Ki-by-N input matrix is treated as N independent channels. The System object generates two power-complementary output signals by adding and subtracting the two polyphase branch outputs respectively. ylow and yhigh are of the same size and data type.

example

Input Arguments

expand all

`x` — Data input
column vector | matrix

Data input, specified as a column vector or a matrix. If the input is a matrix, each column is treated as an independent channel.

The number of rows in the input signal Ki can be arbitrary and does not have to be a multiple of 2. (since R2023b)

This object supports variable-size input signal, that is, the frame length (number of rows) of the signal can change even when the object is locked. However, the number of channels (columns) must remain constant.

Data Types: single | double
Complex Number Support: Yes

Output Arguments

expand all

`ylow` — Lowpass subband of decimator output
column vector | matrix

Lowpass subband of decimator output, returned as a column vector or a matrix. The output, ylow is a lowpass halfband filtered and downsampled version of the input x. Due to the halfband nature of the filter, the downsampling factor is always 2.

When the input is of size K_i-by-N, and K_i is not a multiple of 2, the lowpass subband has an upper bound size of ceil(K_i/2)-by-N. (since R2023b)

If K_i is a multiple of 2, then the lowpass subband is of size (K_i/2)-by-N. The number of channels (columns) does not change.

Data Types: single | double
Complex Number Support: Yes

`yhigh` — Highpass subband of decimator output
column vector | matrix

Highpass subband of decimator output, returned as a column vector or a matrix. The output, yhigh is a highpass halfband filtered and downsampled version of the input x. Due to the halfband nature of the filter, the downsampling factor is always 2.

When the input is of size K_i-by-N, and K_i is not a multiple of 2, the highpass subband has an upper bound size of ceil(K_i/2)-by-N. (since R2023b)

If K_i is a multiple of 2, then the highpass subband is of size (K_i/2)-by-N. The number of channels (columns) does not change.

Data Types: single | double
Complex Number Support: Yes

Object Functions

To use an object function, specify the System object as the first input argument. For example, to release system resources of a System object named obj, use this syntax:

release(obj)

expand all

Specific to `dsp.IIRHalfbandDecimator`

`freqz`	Frequency response of discrete-time filter System object
`freqzmr`	Compute DTFT approximation of impulse response of multirate or single-rate filter
`filterAnalyzer`	Analyze filters with Filter Analyzer app
`info`	Information about filter System object
`cost`	Estimate cost of implementing filter System object
`polyphase`	Polyphase decomposition of multirate filter
`outputDelay`	Determine output delay of single-rate or multirate filter

Common to All System Objects

`step`	Run System object algorithm
`release`	Release resources and allow changes to System object property values and input characteristics
`reset`	Reset internal states of System object

Examples

collapse all

Frequency Response of Quasi-Linear Phase IIR Halfband Decimator

Open Live Script

Create a minimum-order lowpass IIR halfband decimation filter. The filter has a transition width of 0.1859 in normalized frequency units and a stopband attenuation of 80 dB.

IIRHalfbandDecim = dsp.IIRHalfbandDecimator(...
    NormalizedFrequency=true,...
    TransitionWidth=0.1859,...
    DesignMethod='Quasi-linear phase')

IIRHalfbandDecim = 
  dsp.IIRHalfbandDecimator with properties:

   Main
          Specification: 'Transition width and stopband attenuation'
        TransitionWidth: 0.1859
    StopbandAttenuation: 80
           DesignMethod: 'Quasi-linear phase'
    NormalizedFrequency: true

  Use get to show all properties

Obtain the filter coefficients.

c = coeffs(IIRHalfbandDecim);

Plot the magnitude and phase response.

freqz(IIRHalfbandDecim)

$Figure contains 2 axes objects. Axes object 1 with title Phase, xlabel Normalized Frequency (\times\pi rad/sample), ylabel Phase (degrees) contains an object of type line. Axes object 2 with title Magnitude, xlabel Normalized Frequency (\times\pi rad/sample), ylabel Magnitude (dB) contains an object of type line.$

Extract Low Frequency Subband from Speech

Open Live Script

Use a halfband analysis filter bank and interpolation filter to extract the low frequency subband from a speech signal.

Note: The audioDeviceWriter System object™ is not supported in MATLAB Online.

Set up the audio file reader, the analysis filter bank, the audio device writer, and the interpolation filter. The sampling rate of the audio data is 22050 Hz. The halfband filter has an order of 21 and a transition width of 2 kHz.

afr = dsp.AudioFileReader('speech_dft.mp3',SamplesPerFrame=1024);

filterspec = "Filter order and transition width";
Order = 21;
TW = 2000;

IIRHalfbandDecim = dsp.IIRHalfbandDecimator(...
    Specification=filterspec,FilterOrder=Order,...
    TransitionWidth=TW,SampleRate=afr.SampleRate);

IIRHalfbandInterp = dsp.IIRHalfbandInterpolator(...
    Specification=filterspec,FilterOrder=Order,...
    TransitionWidth=TW,SampleRate=afr.SampleRate/2);

ap = audioDeviceWriter(SampleRate=afr.SampleRate);

View the magnitude response of the halfband filter.

filterAnalyzer(IIRHalfbandDecim)

Read the speech signal from the audio file in frames of 1024 samples. Filter the speech signal into lowpass and highpass subbands with a halfband frequency of 5512.5 Hz. Reconstruct a lowpass approximation of the speech signal by interpolating the lowpass subband. Play the filtered output.

while ~isDone(afr)
  audioframe = afr();
  xlo = IIRHalfbandDecim(audioframe);
  ylow = IIRHalfbandInterp(xlo);
  ap(ylow);
end

Wait until the audio file ends, and then close the input file and release the audio output resource.

release(afr);           
release(ap);

Design and Implement IIR Halfband Decimator

Open Live Script

Design an elliptic IIR halfband decimator object of order 31 and a transition width of 0.1 using the designHalfbandIIR function. Set the Verbose argument to true.

hbIIR = designHalfbandIIR(FilterOrder=31,SystemObject=true,...
    Structure='decim',Verbose=true)

designHalfbandIIR(FilterOrder=31, DesignMethod="butter", Structure="decim", Datatype="double", SystemObject=true, Passband="lowpass")

hbIIR = 
  dsp.IIRHalfbandDecimator with properties:

   Main
                   Specification: 'Coefficients'
                       Structure: 'Minimum multiplier'
              HasPureDelayBranch: false
            AllpassCoefficients1: [8x1 double]
            AllpassCoefficients2: [7x1 double]
    HasTrailingFirstOrderSection: false

  Use get to show all properties

Create a dsp.DynamicFilterVisualizer object and visualize the magnitude response of the filter.

dfv = dsp.DynamicFilterVisualizer(NormalizedFrequency=true,YLimits=[-400 200]);
dfv(hbIIR);

The input is a cosine wave.

Fs = 1;
Fc = 0.03;
input = cos(2*pi*Fc*(0:39)'/Fs);

Decimate the cosine signal using the IIR halfband decimator.

output = hbIIR(input);

Plot the original and decimated signals. In order to plot the two signals in the same plot, you must account for the output delay introduced by the IIR halfband decimator and the scaling introduced by the filter. Use the outputDelay function to compute the delay introduced by the decimator. Shift the output by this delay value.

Visualize the input and the resampled signals. Due to the decimation factor of 2, the output samples coincide with every other input sample.

[delay,FsOut] = outputDelay(hbIIR,FsIn=Fs,Fc=Fc)

delay = 
9.9900

FsOut = 
0.5000

nInput = (0:length(input)-1);
tOutput = (0:length(output)-1)/FsOut-delay;
stem(tOutput,output,'filled',MarkerSize=4); hold on;
stem(nInput,input); hold off;
xlim([-10,25])
legend('Decimated by 2','Input signal','Location','best');

Figure contains an axes object. The axes object contains 2 objects of type stem. These objects represent Decimated by 2, Input signal.

Two-Channel Filter Bank

Open Live Script

Use a halfband decimator and interpolator to implement a two-channel filter bank. This example uses an audio file input and shows that the power spectrum of the filter bank output does not differ significantly from the input.

Note: The audioDeviceWriter System object™ is not supported in MATLAB Online.

Set up the audio file reader and audio device writer. Construct the IIR halfband decimator and interpolator. Finally, set up the spectrum analyzer to display the power spectra of the filter-bank input and output.

AF = dsp.AudioFileReader('speech_dft.mp3',SamplesPerFrame=1024);
AP = audioDeviceWriter(SampleRate=AF.SampleRate);

filterspec = "Filter order and transition width";
Order = 51;
TW = 2000;

IIRHalfbandDecim = dsp.IIRHalfbandDecimator(...
    Specification=filterspec,FilterOrder=Order,...
    TransitionWidth=TW,SampleRate=AF.SampleRate);

IIRHalfbandInterp = dsp.IIRHalfbandInterpolator(...
    Specification=filterspec,FilterOrder=Order,...
    TransitionWidth=TW,SampleRate=AF.SampleRate/2,...
    FilterBankInputPort=true);

SpecAna = spectrumAnalyzer(SampleRate=AF.SampleRate,...
    PlotAsTwoSidedSpectrum=false,...
    ShowLegend=true,...
    ChannelNames={'Input signal','Filtered output signal'});

Read the audio 1024 samples at a time. Filter the input to obtain the lowpass and highpass subband signals decimated by a factor of two. This is the analysis filter bank. Use the halfband interpolator as the synthesis filter bank. Display the running power spectrum of the audio input and the output of the synthesis filter bank. Play the output.

while ~isDone(AF)
    audioInput = AF();
    [xlo,xhigh] = IIRHalfbandDecim(audioInput);
    audioOutput = IIRHalfbandInterp(xlo,xhigh);
    spectrumInput = [audioInput audioOutput];
    SpecAna(spectrumInput);
    AP(audioOutput);
end

release(AF);
release(AP);
release(SpecAna);

Filter Input into Lowpass and Highpass Subbands

Open Live Script

Create a halfband decimator. Use a minimum-order design with a transition width of 0.0952 in normalized frequency units and a stopband attenuation of 60 dB.

IIRHalfbanddecim = dsp.IIRHalfbandDecimator(...
    NormalizedFrequency=true,...
    Specification='Transition width and stopband attenuation',...
    TransitionWidth=0.0952,...
    StopbandAttenuation=60);

Filter a two-channel input into lowpass and highpass subbands. The input signal can be of arbitrary frame size, that is, the number of input rows does not have to be a multiple of 2.

x = randn(1025,2);
[ylow,yhigh] = IIRHalfbanddecim(x);

Algorithms

expand all

Polyphase Implementation with Halfband Filters

When you filter your signal, the IIR halfband decimator uses an efficient polyphase implementation for halfband filters. You can use the polyphase implementation to move the downsample operation before filtering. This change enables you to filter at a lower sampling rate.

IIR halfband filters are generally modeled using two parallel allpass filter branches.

$H (z) = 0.5 * [A_{1} (z^{2}) + z^{- 1} A_{2} (z^{2})]$

Elliptic Design

The allpass filters for elliptic IIR halfband filter are given as

$A_{1} (z) = \prod_{k = 1}^{K_{1}} \frac{a_{k}^{(1)} + z^{- 1}}{1 + a_{k}^{(1)} z^{- 1}}$

$A_{2} (z) = \prod_{k = 1}^{K_{2}} \frac{a_{k}^{(2)} + z^{- 1}}{1 + a_{k}^{(2)} z^{- 1}}$

Quasi-Linear Phase Design

To achieve a near-linear phase response for IIR halfband filters, make one of the branches a pure delay. In this design, the cost of the filter increases.

The allpass filters for the quasi-linear phase IIR halfband filter are

$A_{1} (z) = z^{- k}$

where k is the length of the delay.

$A_{2} (z) = \prod_{K = 1}^{K_{2}^{(1)}} \frac{a_{k} + z^{- 1}}{1 + a_{k} z^{- 1}} \prod_{K = 1}^{K_{2}^{(2)}} \frac{c_{k} + b_{k} z^{- 1} + z^{- 2}}{1 + b_{k} z^{- 1} + c_{k} z^{- 2}}$

where N is the order of the IIR halfband filter.

You can represent filtering the input signal and then downsampling it by 2 using this figure.

Using the multirate noble identity for downsampling, you can move the downsampling operation before the filtering operation. This change enables you to filter at a lower rate.

To implement the halfband decimator efficiently, this algorithm replaces the delay block and downsampling operator with a commutator switch. When the first input sample is delivered, the commutator switch feeds this input to the first branch and the halfband decimator computes the first output value. As more input samples come in, the switch delivers one sample at a time to each branch alternatively. The decimator generates output every time the first branch generates an output. This halves the sampling rate of the input signal.

Analysis Filter Bank

The transfer function of the complementary highpass filter branch of the analysis filter bank is given by:

$G (z) = 0.5 * [A_{1} (z^{2}) - z^{- 1} A_{2} (z^{2})]$

You can represent the analysis filter bank as in this diagram.

The IIR halfband decimator generates two power-complementary output signals by adding and subtracting the two polyphase branch outputs respectively.

For more information on filter banks, see Overview of Filter Banks.

To summarize, the IIR halfband decimator:

Decimates the input prior to filtering.
Acts as an analysis filter bank.
Has a nonlinear phase response and uses few coefficients with the elliptic design method.
Has near-linear phase response at the cost of additional coefficients with the quasi-linear phase design method, where one of the branches is a pure delay

References

[1] Lang, M. Allpass Filter Design and Applications. IEEE Transactions on Signal Processing. Vol. 46, No. 9, Sept 1998, pp. 2505–2514.

[2] Harris, F.J. Multirate Signal Processing for Communication Systems. Prentice Hall. 2004, pp. 208–209.

[3] Regalia, Phillip A., Sanjit K. Mitra, and P. P. Vaidyanathan. "The Digital All-Pass Filter: A Versatile Signal Processing Building Block." Proceedings of the IEEE. Vol. 76, Number 1, 1988, pp. 19-37.

Extended Capabilities

C/C++ Code Generation
Generate C and C++ code using MATLAB® Coder™.

Usage notes and limitations:

See System Objects in MATLAB Code Generation (MATLAB Coder).

This object supports code generation for ARM^® Cortex^®-M and ARM Cortex-A processors.

Version History

Introduced in R2015b

expand all

R2023b: Support for normalized frequencies

When you set the NormalizedFrequency property to true, you must specify the transition width in normalized frequency units (0 to 1).

When you set the NormalizedFrequency property to true while creating the object and you do not set the transition width, the object automatically sets the default transition width to normalized frequency units using the default sample rate of 44100 Hz.

iirhalfbanddecim = dsp.IIRHalfbandDecimator(NormalizedFrequency=true)

iirhalfbanddecim = 
  dsp.IIRHalfbandDecimator with properties:

          Specification: 'Transition width and stopband attenuation'
        TransitionWidth: 0.1859
    StopbandAttenuation: 80
           DesignMethod: 'Elliptic'
    NormalizedFrequency: true

When you set the NormalizedFrequency property to true after you create the object, you must specify the transition width in normalized units before you run the object algorithm.

iirhalfbanddecim = dsp.IIRHalfbandDecimator

iirhalfbanddecim = 
  dsp.IIRHalfbandDecimator with properties:

          Specification: 'Transition width and stopband attenuation'
        TransitionWidth: 4100
    StopbandAttenuation: 80
           DesignMethod: 'Elliptic'
    NormalizedFrequency: false
             SampleRate: 44100

To specify the normalized frequency values, set NormalizedFrequency to true and manually convert the frequency values in Hz to normalized values using the input sample rate in Hz. For example, if the input sample rate is 44100 Hz, you can compute the corresponding values in normalized units using these equations.

iirhalfbanddecim.NormalizedFrequency = true;
iirhalfbanddecim.TransitionWidth = 4100/(44100/2)

iirhalfbanddecim = 
  dsp.IIRHalfbandDecimator with properties:

          Specification: 'Transition width and stopband attenuation'
        TransitionWidth: 0.1859
    StopbandAttenuation: 80
           DesignMethod: 'Elliptic'
    NormalizedFrequency: true

R2023b: Support for arbitrary input frame length

This object supports an input signal with an arbitrary frame length, so the input frame length does not have to be a multiple of the decimation factor 2.

When you generate code, to support arbitrary frame length for fixed-size signals, you must set the AllowArbitraryInputLength property to true while generating code.

dsp.IIRHalfbandDecimator

Description

Creation

Syntax

Description

Properties

Main Properties

Specification — Filter design parameters "Transition width and stopband attenuation" (default) | "Filter order and stopband attenuation" | "Filter order and transition width" | "Coefficients"

FilterOrder — Order of the IIR halfband filter 9 (default) | positive scalar integer

Dependencies

StopbandAttenuation — Minimum attenuation needed in stopband 80 (default) | positive real scalar

Dependencies

TransitionWidth — Transition width 4100 (default) | positive real scalar

Dependencies

DesignMethod — Design method "Elliptic" (default) | "Quasi-linear phase"

Dependencies

NormalizedFrequency — Flag to set frequencies in normalized units false (default) | true

Dependency

SampleRate — Input sample rate 44100 (default) | positive real scalar

Dependency

Structure — Internal allpass filter implementation structure "Minimum multiplier" (default) | "Wave Digital Filter"

Dependencies

AllpassCoefficients1 — Allpass polynomial filter coefficients of first branch [0.1284563; 0.7906755] (default) | [0.1284563 0.1534; 0.7906755 0.6745]

Dependencies

AllpassCoefficients2 — Allpass polynomial filter coefficients of second branch [0.4295667] (default) | [0.7906755 0.1534]

Dependencies

WDFCoefficients1 — Allpass filter coefficients of first branch in Wave Digital Filter form [0.1284563; 0.7906755] (default) | [0.1284563 0.1534; 0.7906755 0.6745]

Dependencies

WDFCoefficients2 — Allpass filter coefficients of second branch in Wave Digital Filter form [0.4295667] (default) | [0.7906755 0.1534]

Dependencies

HasPureDelayBranch — Make first branch a pure delay false (default) | true

Dependencies

Delay — Length of delay 1 (default) | finite positive scalar

Dependencies

HasTrailingFirstOrderSection — Treat the last section of the second branch as first order false (default) | true

Dependencies

Code Generation Properties

AllowArbitraryInputLength — Allow arbitrary input length in generated code false (default) | true

Usage

Syntax

Description

Input Arguments

x — Data input column vector | matrix

Output Arguments

ylow — Lowpass subband of decimator output column vector | matrix

yhigh — Highpass subband of decimator output column vector | matrix

Object Functions

Specific to dsp.IIRHalfbandDecimator

Common to All System Objects

Examples

Frequency Response of Quasi-Linear Phase IIR Halfband Decimator

Extract Low Frequency Subband from Speech

Design and Implement IIR Halfband Decimator

Two-Channel Filter Bank

Filter Input into Lowpass and Highpass Subbands

Algorithms

Polyphase Implementation with Halfband Filters

References

Extended Capabilities

C/C++ Code Generation Generate C and C++ code using MATLAB® Coder™.

Version History

R2023b: Support for normalized frequencies

R2023b: Support for arbitrary input frame length

See Also

Functions

Objects

Blocks

Topics

`Specification` — Filter design parameters
`"Transition width and stopband attenuation"` (default) | `"Filter order and stopband attenuation"` | `"Filter order and transition width"` | `"Coefficients"`

`FilterOrder` — Order of the IIR halfband filter
9 (default) | positive scalar integer

`StopbandAttenuation` — Minimum attenuation needed in stopband
80 (default) | positive real scalar

`TransitionWidth` — Transition width
4100 (default) | positive real scalar

`DesignMethod` — Design method
`"Elliptic"` (default) | `"Quasi-linear phase"`

`NormalizedFrequency` — Flag to set frequencies in normalized units
`false` (default) | `true`

`SampleRate` — Input sample rate
44100 (default) | positive real scalar

`Structure` — Internal allpass filter implementation structure
`"Minimum multiplier"` (default) | `"Wave Digital Filter"`

`AllpassCoefficients1` — Allpass polynomial filter coefficients of first branch
`[0.1284563; 0.7906755]` (default) | `[0.1284563 0.1534; 0.7906755 0.6745]`

`AllpassCoefficients2` — Allpass polynomial filter coefficients of second branch
`[0.4295667]` (default) | `[0.7906755 0.1534]`

`WDFCoefficients1` — Allpass filter coefficients of first branch in Wave Digital Filter form
`[0.1284563; 0.7906755]` (default) | `[0.1284563 0.1534; 0.7906755 0.6745]`

`WDFCoefficients2` — Allpass filter coefficients of second branch in Wave Digital Filter form
`[0.4295667]` (default) | `[0.7906755 0.1534]`

`HasPureDelayBranch` — Make first branch a pure delay
`false` (default) | `true`

`Delay` — Length of delay
`1` (default) | finite positive scalar

`HasTrailingFirstOrderSection` — Treat the last section of the second branch as first order
`false` (default) | `true`

`AllowArbitraryInputLength` — Allow arbitrary input length in generated code
`false` (default) | `true`

`x` — Data input
column vector | matrix

`ylow` — Lowpass subband of decimator output
column vector | matrix

`yhigh` — Highpass subband of decimator output
column vector | matrix

Specific to `dsp.IIRHalfbandDecimator`

C/C++ Code Generation
Generate C and C++ code using MATLAB® Coder™.