dsp.CICCompensationDecimator

Compensate for CIC decimation filter using FIR decimator

Description

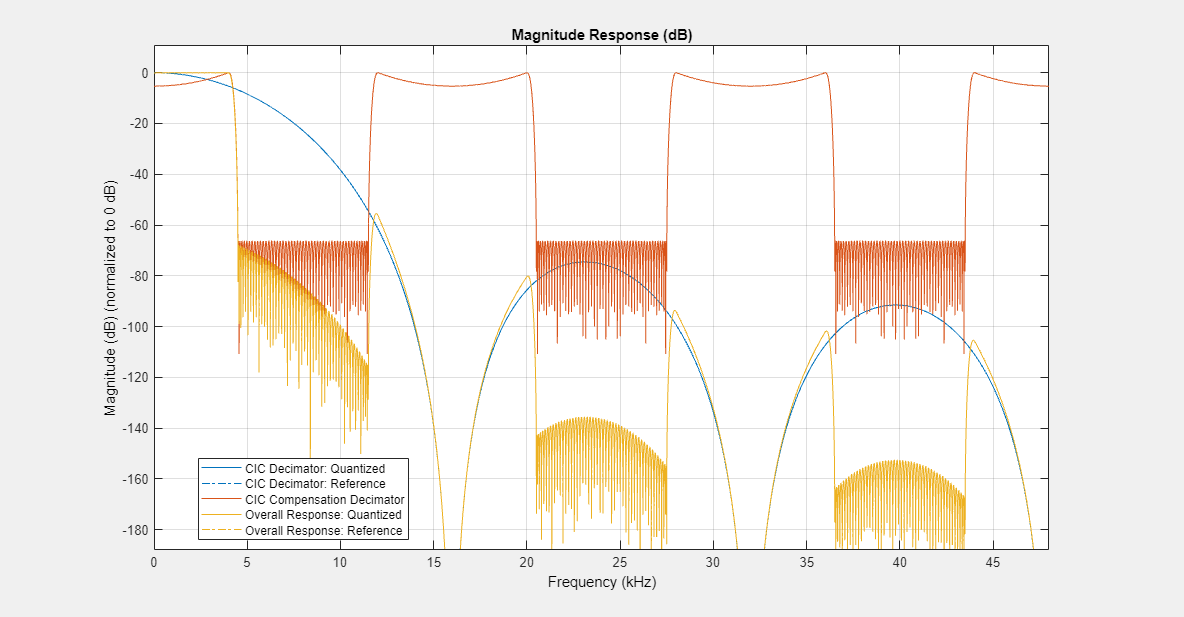
You can compensate for the shortcomings of a CIC decimator, namely its passband droop and wide transition region, by following it with a compensation decimator. This System object™ lets you design and use such a filter.

To compensate for the shortcomings of a CIC filter using an FIR decimator:

Create the dsp.CICCompensationDecimator object and set its properties.
Call the object with arguments, as if it were a function.

To learn more about how System objects work, see What Are System Objects?

Creation

Syntax

ciccompdec = dsp.CICCompensationDecimator

ciccompdec = dsp.CICCompensationDecimator(decim)

ciccompdec = dsp.CICCompensationDecimator(cic)

ciccompdec = dsp.CICCompensationDecimator(cic,decim)

ciccompdec = dsp.CICCompensationDecimator(___,Name=Value)

Description

ciccompdec = dsp.CICCompensationDecimator returns a System object, ciccompdec, that applies an FIR decimator to each channel of an input signal. Using the properties of the object, the decimation filter can be designed to compensate for a preceding CIC filter.

ciccompdec = dsp.CICCompensationDecimator(decim) returns a CIC compensation decimator System object, with the DecimationFactor property set to decim.

ciccompdec = dsp.CICCompensationDecimator(cic) returns a CIC compensation decimator System object, with the CICRateChangeFactor, CICNumSections, and CICDifferentialDelay properties specified in the dsp.CICDecimator System object, cic.

ciccompdec = dsp.CICCompensationDecimator(cic,decim) returns a CIC compensation decimator System object, ciccompdec, with the CICRateChangeFactor, CICNumSections, and CICDifferentialDelay properties specified in the dsp.CICDecimator System object cic, and the DecimationFactor property set to decim.

ciccompdec = dsp.CICCompensationDecimator(___,Name=Value) returns a CIC compensation decimator object with properties specified by one or more name-value pair arguments. Unspecified properties have default values.

example

Properties

expand all

Unless otherwise indicated, properties are nontunable, which means you cannot change their values after calling the object. Objects lock when you call them, and the release function unlocks them.

If a property is tunable, you can change its value at any time.

For more information on changing property values, see System Design in MATLAB Using System Objects.

`CICRateChangeFactor` — Rate-change factor of the CIC filter being compensated
`2` (default) | positive integer scalar

Specify the rate-change factor of the CIC filter being compensated as a positive integer scalar.

`CICNumSections` — Number of sections of the CIC filter being compensated
`2` (default) | positive integer scalar

Specify the number of sections of the CIC filter being compensated as a positive integer scalar.

`CICDifferentialDelay` — Differential delay of the CIC filter being compensated
`1` (default) | positive integer scalar

Specify the differential delay of the CIC filter being compensated as a positive integer scalar.

`DecimationFactor` — Decimation factor of compensator
`2` (default) | positive integer scalar

Specify the decimation factor of the compensator System object as a positive integer scalar.

`NormalizedFrequency` — Option to set frequencies in normalized units
`false` (default) | `true`

Since R2024a

Option to set frequencies in normalized units, specified as one of these values:

true –– The passband frequency Fpass and stopband frequency Fstop must be in the normalized frequency units and must be in the range Fpass < Fstop < 1.0.

When you set the NormalizedFrequency property to true while creating the object and you do not set the passband and stopband frequencies, the object automatically sets the default values to normalized frequency units using the default sample rate of 1200 kHz.

ciccompdec = dsp.CICCompensationDecimator(NormalizedFrequency=true)

ciccompdec = 
  dsp.CICCompensationDecimator with properties:

      CICRateChangeFactor: 2
           CICNumSections: 2
     CICDifferentialDelay: 1
         DecimationFactor: 2
      NormalizedFrequency: true
    DesignForMinimumOrder: true
        PassbandFrequency: 0.1667
        StopbandFrequency: 0.6667
           PassbandRipple: 0.1000
      StopbandAttenuation: 60

When you set the NormalizedFrequency property to true after you create the object, you must specify the passband and stopband frequencies in normalized units before you run the object algorithm.

ciccompdec = dsp.CICCompensationDecimator

ciccompdec = 
  dsp.CICCompensationDecimator with properties:

      CICRateChangeFactor: 2
           CICNumSections: 2
     CICDifferentialDelay: 1
         DecimationFactor: 2
      NormalizedFrequency: false
    DesignForMinimumOrder: true
        PassbandFrequency: 100000
        StopbandFrequency: 400000
           PassbandRipple: 0.1000
      StopbandAttenuation: 60
               SampleRate: 1200000

To specify the normalized frequency value, set NormalizedFrequency to true and manually convert the frequency value in Hz to the normalized value using the input sample rate in Hz. For example, if the input sample rate Fs is 1200 kHz, the corresponding passband frequency value in normalized units is Fpass_Hz/(Fs/2) and the corresponding stopband frequency in normalized units is Fstop_Hz/(Fs/2).

ciccompdec = dsp.CICCompensationDecimator;
ciccompdec.NormalizedFrequency = true;
ciccompdec.PassbandFrequency = 100000/(1200000/2);
ciccompdec.StopbandFrequency = 400000/(1200000/2)

ciccompdec = 
  dsp.CICCompensationDecimator with properties:

      CICRateChangeFactor: 2
           CICNumSections: 2
     CICDifferentialDelay: 1
         DecimationFactor: 2
      NormalizedFrequency: true
    DesignForMinimumOrder: true
        PassbandFrequency: 0.1667
        StopbandFrequency: 0.6667
           PassbandRipple: 0.1000
      StopbandAttenuation: 60

false –– The passband and stopband frequency values are in Hz. You can specify the input sample rate through the SampleRate property.

Data Types: logical

`DesignForMinimumOrder` — Design filter of minimum order or of specified order
`true` (default) | `false`

Specify whether to design a filter of minimum order or a filter of specified order as a logical scalar. The default is true, which corresponds to a filter of minimum order.

`FilterOrder` — Order of decimation compensator filter
12 (default) | positive integer scalar

Specify the order of the decimation compensator filter as a positive integer scalar.

Dependencies

To enable this property, set the DesignForMinimumOrder property to false.

`PassbandFrequency` — Passband edge frequency
`100000` (default) | positive real scalar

Passband edge frequency Fpass, specified as a positive real scalar in Hz or in normalized frequency units (since R2024a).

If you set the NormalizedFrequency property to:

false –– The value of the passband frequency is in Hz and must be in the range Fpass < Fstop < Fs/2, where Fstop is the stopband frequency and Fs is the input sample rate.

true –– The value of the passband frequency is in normalized frequency units and must be in the range Fpass < Fstop < 1.0.

When you set the NormalizedFrequency property to true while creating the object and you do not set the passband frequency, the object automatically sets the default passband frequency to normalized frequency units using the default sample rate of 1200 kHz.

ciccompdec = dsp.CICCompensationDecimator(NormalizedFrequency=true)

ciccompdec = 
  dsp.CICCompensationDecimator with properties:

      CICRateChangeFactor: 2
           CICNumSections: 2
     CICDifferentialDelay: 1
         DecimationFactor: 2
      NormalizedFrequency: true
    DesignForMinimumOrder: true
        PassbandFrequency: 0.1667
        StopbandFrequency: 0.6667
           PassbandRipple: 0.1000
      StopbandAttenuation: 60

When you set the NormalizedFrequency property to true after you create the object, you must specify the passband frequency in normalized units before you run the object algorithm.

ciccompdec = dsp.CICCompensationDecimator

ciccompdec = 
  dsp.CICCompensationDecimator with properties:

      CICRateChangeFactor: 2
           CICNumSections: 2
     CICDifferentialDelay: 1
         DecimationFactor: 2
      NormalizedFrequency: false
    DesignForMinimumOrder: true
        PassbandFrequency: 100000
        StopbandFrequency: 400000
           PassbandRipple: 0.1000
      StopbandAttenuation: 60
               SampleRate: 1200000

To specify the normalized frequency value, set NormalizedFrequency to true and manually convert the frequency value in Hz to the normalized value using half the input sample rate in Hz. For example, if the input sample rate Fs is 1200 kHz, the corresponding passband frequency value in normalized units is Fpass_Hz/(Fs/2).

ciccompdec.NormalizedFrequency = true;
ciccompdec.PassbandFrequency = 100000/(1200000/2)

ciccompdec = 
  dsp.CICCompensationDecimator with properties:

      CICRateChangeFactor: 2
           CICNumSections: 2
     CICDifferentialDelay: 1
         DecimationFactor: 2
      NormalizedFrequency: true
    DesignForMinimumOrder: true
        PassbandFrequency: 0.1667
        StopbandFrequency: 400000
           PassbandRipple: 0.1000
      StopbandAttenuation: 60

(since R2024a)

`StopbandFrequency` — Stopband edge frequency
`400000` (default) | positive real scalar

Stopband edge frequency Fstop, specified as a positive real scalar in Hz or in normalized frequency units (since R2024a).

If you set the NormalizedFrequency property to:

false –– The value of the stopband frequency is in Hz and must be in the range Fpass < Fstop < Fs/2, where Fpass is the passband frequency and Fs is the input sample rate.

true –– The value of the stopband frequency is in normalized frequency units and must be in the range Fpass < Fstop < 1.0.

When you set the NormalizedFrequency property to true while creating the object and you do not set the stopband frequency, the object automatically sets the default stopband frequency to normalized frequency units using the default sample rate of 1200 kHz.

ciccompdec = dsp.CICCompensationDecimator(NormalizedFrequency=true)

ciccompdec = 
  dsp.CICCompensationDecimator with properties:

      CICRateChangeFactor: 2
           CICNumSections: 2
     CICDifferentialDelay: 1
         DecimationFactor: 2
      NormalizedFrequency: true
    DesignForMinimumOrder: true
        PassbandFrequency: 0.1667
        StopbandFrequency: 0.6667
           PassbandRipple: 0.1000
      StopbandAttenuation: 60

When you set the NormalizedFrequency property to true after you create the object, you must specify the passband frequency in normalized units before you run the object algorithm.

ciccompdec = dsp.CICCompensationDecimator

ciccompdec = 
  dsp.CICCompensationDecimator with properties:

      CICRateChangeFactor: 2
           CICNumSections: 2
     CICDifferentialDelay: 1
         DecimationFactor: 2
      NormalizedFrequency: false
    DesignForMinimumOrder: true
        PassbandFrequency: 100000
        StopbandFrequency: 400000
           PassbandRipple: 0.1000
      StopbandAttenuation: 60
               SampleRate: 1200000

To specify the normalized frequency value, set NormalizedFrequency to true and manually convert the frequency value in Hz to the normalized value using half the input sample rate in Hz. For example, if the input sample rate Fs is 1200 kHz, the corresponding stopband frequency value in normalized units is Fstop_Hz/(Fs/2).

ciccompdec.NormalizedFrequency = true;
ciccompdec.StopbandFrequency = 400000/(1200000/2)

ciccompdec = 
  dsp.CICCompensationDecimator with properties:

      CICRateChangeFactor: 2
           CICNumSections: 2
     CICDifferentialDelay: 1
         DecimationFactor: 2
      NormalizedFrequency: true
    DesignForMinimumOrder: true
        PassbandFrequency: 100000
        StopbandFrequency: 0.6667
           PassbandRipple: 0.1000
      StopbandAttenuation: 60

(since R2024a)

`PassbandRipple` — Filter passband ripple in decibels
`0.1` (default) | positive real scalar

Specify the filter passband ripple as a positive real scalar expressed in decibels.

`StopbandAttenuation` — Filter stopband attenuation in decibels
`60` (default) | positive real scalar

Specify the filter stopband attenuation as a positive real scalar expressed in decibels.

`SampleRate` — Input sample rate in hertz
`1200000` (default) | positive real scalar

Specify the input sample rate Fs as a positive real scalar expressed in hertz.

Dependencies

To enable this property, set the NormalizedFrequency property to false.

Data Types: single | double

Fixed-Point Properties

`RoundingMethod` — Rounding method for output fixed-point operations
`'Floor'` (default) | `'Ceiling'` | `'Convergent'` | `'Nearest'` | `'Round'` | `'Simplest'` | `'Zero'`

Rounding method for output fixed-point operations, specified as a character vector. For more information on the rounding modes, see Precision and Range.

`CoefficientsDataType` — Word and fraction lengths of coefficients
`numerictype(1,16)` (default) | `numerictype` object

Word and fraction lengths of coefficients, specified as a signed or unsigned numerictype object. The default, numerictype(1,16) corresponds to a signed numeric type object with 16-bit coefficients and a fraction length determined based on the coefficient values, to give the best possible precision.

This property is not tunable.

Word length of the output is same as the word length of the input. Fraction length of the output is computed such that the entire dynamic range of the output can be represented without overflow. For details on how the fraction length of the output is computed, see Fixed-Point Precision Rules for Avoiding Overflow in FIR Filters.

Usage

Syntax

y = ciccompdecim(x)

Description

y = ciccompdecim(x) returns the filtered and downsampled values, y, of the input signal, x.

example

Input Arguments

expand all

`x` — Data input
vector | matrix

Data input, specified as a vector or a matrix. The System object treats a K_i-by-N input matrix as N independent channels, decimating each channel over the first dimension.

The number of input rows K_i can be arbitrary and does not have to be a multiple of the decimation factor.

This object supports variable-size input signals, that is, the frame length (number of rows) of the signal can change even when the object is locked. However, the number of channels (columns) must remain constant.

This object does not support complex unsigned fixed-point data.

Output Arguments

expand all

`y` — Filtered and downsampled signal
vector | matrix

Filtered and downsampled signal, returned as a vector or matrix.

When the input is of size K_i-by-N, and K_i is not a multiple of the decimation factor M, the output signal has an upper bound size of ceil(K_i/M)-by-N. If K_i is a multiple of the decimation factor, then the output is of size (K_i/M)-by-N. The number of channels (columns) does not change.

Object Functions

To use an object function, specify the System object as the first input argument. For example, to release system resources of a System object named obj, use this syntax:

release(obj)

expand all

Specific to `dsp.CICCompensationDecimator`

`freqz`	Frequency response of discrete-time filter System object
`freqzmr`	Compute DTFT approximation of impulse response of multirate or single-rate filter
`filterAnalyzer`	Analyze filters with Filter Analyzer app
`info`	Information about filter System object
`cost`	Estimate cost of implementing filter System object
`coeffs`	Returns the filter System object coefficients in a structure
`outputDelay`	Determine output delay of single-rate or multirate filter
`polyphase`	Polyphase decomposition of multirate filter
`generatehdl`	Generate HDL code for quantized DSP filter (requires Filter Design HDL Coder) (To be removed)

Common to All System Objects

`step`	Run System object algorithm
`release`	Release resources and allow changes to System object property values and input characteristics
`reset`	Reset internal states of System object

Examples

collapse all

Impulse and Frequency Response of CIC Compensation Decimator

Open Live Script

Create a dsp.CICCompensationDecimator object with default settings. While creating the object, set the NormalizedFrequency property to true so that the passband and the stopband frequencies are in normalized frequency units.

CICCompDecim = dsp.CICCompensationDecimator(...
    NormalizedFrequency=true)

CICCompDecim = 
  dsp.CICCompensationDecimator with properties:

      CICRateChangeFactor: 2
           CICNumSections: 2
     CICDifferentialDelay: 1
         DecimationFactor: 2
      NormalizedFrequency: true
    DesignForMinimumOrder: true
        PassbandFrequency: 0.1667
        StopbandFrequency: 0.6667
           PassbandRipple: 0.1000
      StopbandAttenuation: 60

  Use get to show all properties

Plot the impulse response.

impz(CICCompDecim)

Figure contains an axes object. The axes object with title Impulse Response, xlabel n (samples), ylabel Amplitude contains an object of type stem.

Plot the magnitude and phase responses.

freqz(CICCompDecim)

$Figure contains 2 axes objects. Axes object 1 with title Phase, xlabel Normalized Frequency (\times\pi rad/sample), ylabel Phase (degrees) contains an object of type line. Axes object 2 with title Magnitude, xlabel Normalized Frequency (\times\pi rad/sample), ylabel Magnitude (dB) contains an object of type line.$

Compensation Decimator Design

This example uses:

Open Live Script

Design a compensation decimator for an existing CIC decimator having six sections and a decimation factor of 6.

CICDecim = dsp.CICDecimator(DecimationFactor=6,...
    NumSections=6)

CICDecim = 
  dsp.CICDecimator with properties:

      DecimationFactor: 6
     DifferentialDelay: 1
           NumSections: 6
    FixedPointDataType: 'Full precision'

Construct the compensation decimator. Specify a decimation factor of 2, an input sample rate of 16 kHz, a passband frequency of 4 kHz, and a stopband frequency of 4.5 kHz.

fs = 16e3;
fPass = 4e3;
fStop = 4.5e3;

CICCompDecim = dsp.CICCompensationDecimator(CICDecim,...
    DecimationFactor=2,PassbandFrequency=fPass,...
    StopbandFrequency=fStop,SampleRate=fs)

CICCompDecim = 
  dsp.CICCompensationDecimator with properties:

      CICRateChangeFactor: 6
           CICNumSections: 6
     CICDifferentialDelay: 1
         DecimationFactor: 2
    DesignForMinimumOrder: true
        PassbandFrequency: 4000
        StopbandFrequency: 4500
           PassbandRipple: 0.1000
      StopbandAttenuation: 60
               SampleRate: 16000

  Show all properties

Visualize the frequency response of the cascade. Normalize all magnitude responses to 0 dB.

filtCasc = dsp.FilterCascade(CICDecim,CICCompDecim);

f = fvtool(CICDecim, CICCompDecim, filtCasc, ...
    Fs=[fs*6 fs fs*6]);

f.NormalizeMagnitudeto1 = 'on';
legend(f,'CIC Decimator','CIC Compensation Decimator', ...
    'Overall Response');

Figure Figure 2: Magnitude Response (dB) contains an axes object. The axes object with title Magnitude Response (dB), xlabel Frequency (kHz), ylabel Magnitude (dB) (normalized to 0 dB) contains 5 objects of type line. These objects represent CIC Decimator: Quantized, CIC Decimator: Reference, CIC Compensation Decimator, Overall Response: Quantized, Overall Response: Reference.

Apply the design to a 1200-sample random input signal. Store the decimated output along the first dimension of the y array.

x = dsp.SignalSource(fi(rand(1200,1),1,16,15),SamplesPerFrame=120);

y = fi(zeros(100,1),1,32,20);

for ind = 1:10
    x2 = CICDecim(x());
    y(((ind-1)*10)+1:ind*10,1) = CICCompDecim(x2);
end

Algorithms

The response of a CIC filter is given by:

$H_{c i c} (ω) = {[\frac{\sin (\frac{R D ω}{2})}{\sin (\frac{ω}{2})}]}^{N}$

R, D, and N are the rate change factor, the differential delay, and the number of sections in the CIC filter, respectively.

After decimation, the CIC response has the form:

$H_{c i c} (ω) = {[\frac{\sin (\frac{D ω}{2})}{\sin (\frac{ω}{2 R})}]}^{N}$

The normalized version of this last response is the one that the CIC compensator needs to compensate. Hence, the passband response of the CIC compensator should take the following form:

$H_{c i c c o m p} (ω) = {[R D \frac{\sin (\frac{ω}{2 R})}{\sin (\frac{D ω}{2})}]}^{N} for ω \leq ω_{p} < π$

where ω_p is the passband frequency of the CIC compensation filter.

Notice that when ω/2R ≪ π, the previous equation for Hciccomp(ω) can be simplified using the fact that sin(x) ≅ x:

$H_{c i c c o m p} (ω) \approx {[\frac{(\frac{D ω}{2})}{\sin (\frac{D ω}{2})}]}^{N} = {[s i n c (\frac{D ω}{2})]}^{- N} for ω \leq ω_{p} < π$

This previous equation is the inverse sinc approximation to the true inverse passband response of the CIC filter.

Extended Capabilities

C/C++ Code Generation
Generate C and C++ code using MATLAB® Coder™.

Usage notes and limitations:

See System Objects in MATLAB Code Generation (MATLAB Coder).
This object supports code generation for ARM^® Cortex^®-M and ARM Cortex-A processors.
In the code you generate from this object, the decimator output is a fixed-size signal if the input signal is fixed size and is a multiple of the decimation factor. If the input is not a multiple of the decimation factor or if the input is a variable-size signal, then the decimator output is of variable-size.

HDL Code Generation
Generate VHDL, Verilog and SystemVerilog code for FPGA and ASIC designs using HDL Coder™.

This object supports HDL code generation with the Filter Design HDL Coder™ product. For workflows and limitations, see Generate HDL Code for Filter System Objects (Filter Design HDL Coder).

Version History

Introduced in R2014b

expand all

R2024a: Support for normalized frequencies

When you set the NormalizedFrequency property to true, you must specify the passband frequency and stopband frequency in normalized frequency units (0 to 1). For more information, see the NormalizedFrequency property description.

R2023a: Support for arbitrary input frame length

This object supports an input signal with an arbitrary frame length, so the input frame length does not have to be a multiple of the decimation factor.

R2023a: Support for variable-size input signal

The input signal to this object can be a variable-size signal, that is, the frame length (number of rows) of the signal can change even when the object is locked. However, the number of channels (columns) must remain constant.

dsp.CICCompensationDecimator

Description

Creation

Syntax

Description

Properties

CICRateChangeFactor — Rate-change factor of the CIC filter being compensated 2 (default) | positive integer scalar

CICNumSections — Number of sections of the CIC filter being compensated 2 (default) | positive integer scalar

CICDifferentialDelay — Differential delay of the CIC filter being compensated 1 (default) | positive integer scalar

DecimationFactor — Decimation factor of compensator 2 (default) | positive integer scalar

NormalizedFrequency — Option to set frequencies in normalized units false (default) | true

DesignForMinimumOrder — Design filter of minimum order or of specified order true (default) | false

FilterOrder — Order of decimation compensator filter 12 (default) | positive integer scalar

Dependencies

PassbandFrequency — Passband edge frequency 100000 (default) | positive real scalar

StopbandFrequency — Stopband edge frequency 400000 (default) | positive real scalar

PassbandRipple — Filter passband ripple in decibels 0.1 (default) | positive real scalar

StopbandAttenuation — Filter stopband attenuation in decibels 60 (default) | positive real scalar

SampleRate — Input sample rate in hertz 1200000 (default) | positive real scalar

Dependencies

Fixed-Point Properties

RoundingMethod — Rounding method for output fixed-point operations 'Floor' (default) | 'Ceiling' | 'Convergent' | 'Nearest' | 'Round' | 'Simplest' | 'Zero'

CoefficientsDataType — Word and fraction lengths of coefficients numerictype(1,16) (default) | numerictype object

Usage

Syntax

Description

Input Arguments

x — Data input vector | matrix

Output Arguments

y — Filtered and downsampled signal vector | matrix

Object Functions

Specific to dsp.CICCompensationDecimator

Common to All System Objects

Examples

Impulse and Frequency Response of CIC Compensation Decimator

Compensation Decimator Design

Algorithms

Extended Capabilities

C/C++ Code Generation Generate C and C++ code using MATLAB® Coder™.

HDL Code Generation Generate VHDL, Verilog and SystemVerilog code for FPGA and ASIC designs using HDL Coder™.

Version History

R2024a: Support for normalized frequencies

R2023a: Support for arbitrary input frame length

R2023a: Support for variable-size input signal

See Also

Functions

Objects

Topics

`CICRateChangeFactor` — Rate-change factor of the CIC filter being compensated
`2` (default) | positive integer scalar

`CICNumSections` — Number of sections of the CIC filter being compensated
`2` (default) | positive integer scalar

`CICDifferentialDelay` — Differential delay of the CIC filter being compensated
`1` (default) | positive integer scalar

`DecimationFactor` — Decimation factor of compensator
`2` (default) | positive integer scalar

`NormalizedFrequency` — Option to set frequencies in normalized units
`false` (default) | `true`

`DesignForMinimumOrder` — Design filter of minimum order or of specified order
`true` (default) | `false`

`FilterOrder` — Order of decimation compensator filter
12 (default) | positive integer scalar

`PassbandFrequency` — Passband edge frequency
`100000` (default) | positive real scalar

`StopbandFrequency` — Stopband edge frequency
`400000` (default) | positive real scalar

`PassbandRipple` — Filter passband ripple in decibels
`0.1` (default) | positive real scalar

`StopbandAttenuation` — Filter stopband attenuation in decibels
`60` (default) | positive real scalar

`SampleRate` — Input sample rate in hertz
`1200000` (default) | positive real scalar

`RoundingMethod` — Rounding method for output fixed-point operations
`'Floor'` (default) | `'Ceiling'` | `'Convergent'` | `'Nearest'` | `'Round'` | `'Simplest'` | `'Zero'`

`CoefficientsDataType` — Word and fraction lengths of coefficients
`numerictype(1,16)` (default) | `numerictype` object

`x` — Data input
vector | matrix

`y` — Filtered and downsampled signal
vector | matrix

Specific to `dsp.CICCompensationDecimator`

C/C++ Code Generation
Generate C and C++ code using MATLAB® Coder™.

HDL Code Generation
Generate VHDL, Verilog and SystemVerilog code for FPGA and ASIC designs using HDL Coder™.