Outlier Removal Techniques with ECG Signals

Introduction

There are many different outlier removal techniques because a rigid definition of an outlier does not exist.

The three techniques explored in this example are:

ECG Signal Source

The ECG signal used in this example is taken from the MIT-BIH Arrhythmia Database. The signal is sampled at 360 Hz. The signal was shifted and scaled to convert it from the raw 12-bit ADC values to real-world values.

For more information on ECG signals, please see the example Real-Time ECG QRS Detection.

Setup

First, create a stream from the ECG signal using the dsp.MatFileReader. Next, create a scope to visualize the raw and filtered signals.

Fs = 360;
frameSize = 500;
fileName = "ecgsig.mat";
winLen = 13; % Window length for the filters.

fileReader = dsp.MatFileReader(Filename=fileName, ...
    VariableName="ecgsig",SamplesPerFrame=frameSize);
scope = timescope(SampleRate=Fs,TimeSpan=2, ...
    LayoutDimensions=[2 1], LineWidth=2);
scope.ActiveDisplay = 1;
scope.Title = "Raw Signal";
scope.YLimits = [-2 2];
scope.ActiveDisplay = 2;
scope.Title = "Filtered Signal";
scope.YLimits = [-2 2];

Outlier Removal Performance of Moving Average Filter

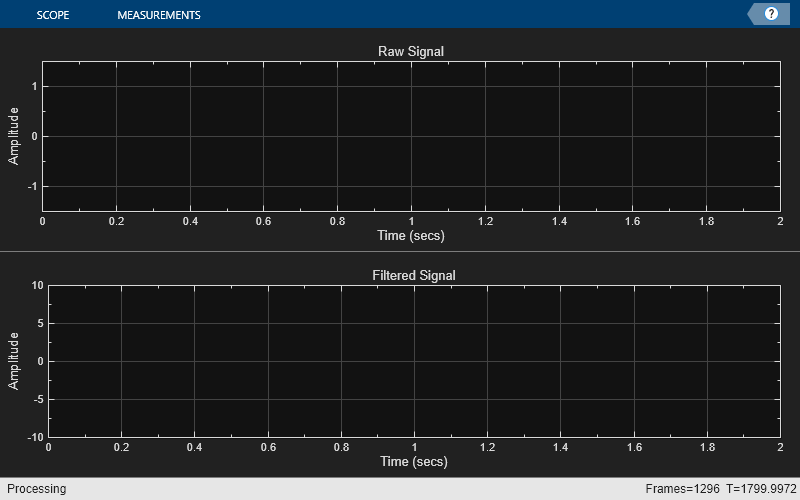
The moving average filter calculates a running mean on the specified window length. This is a relatively simple calculation compared to the other two filters. However, this will smooth both the signal and the outliers. This causes the peak in the ECG signal to be smoothed to roughly a third of its original magnitude.

movAvg = dsp.MovingAverage(winLen);
while ~isDone(fileReader)
    x = fileReader();
    y = movAvg(x);
    scope(x,y);
end
release(scope);

% Clean up
reset(fileReader);

Outlier Removal Performance of Median Filter

The Median Filter is sometimes a better choice since it is less sensitive to outliers than the Moving Average Filter. However, as can be seen in the scope below, it can cause "steps" to appear at extremes in the signal where the local median does not change. This means that the window length of the filter must be carefully considered.

medFilt = dsp.MedianFilter(winLen);
while ~isDone(fileReader)
    x = fileReader();
    y = medFilt(x);
    scope(x,y);
end
release(scope);

% Clean up
reset(fileReader);

Outlier Removal Performance of Hampel Filter

The Hampel Filter has an additional threshold parameter that can be set. Below, it is set to one, meaning that any sample that is more than one standard deviation away from the local median will be classified as an outlier. Both the threshold and the window length can be changed to remove outliers from the input signal without distorting the original signal.

thres = 1;
hampFilt = dsp.HampelFilter(winLen,thres);
while ~isDone(fileReader)
    x = fileReader();
    y = hampFilt(x);
    scope(x,y);
end
release(scope);

% Clean up
reset(fileReader);

Conclusion

All three of the above filters can be used for outlier removal. The noise distribution of the outliers and the window length both effect the filter's performance. This must be taken into consideration when selecting a filter for outlier removal in a specific application.