Specifying Univariate Lag Operator Polynomials Interactively

Consider building a predictive, univariate time series model (conditional mean, conditional variance, or regression model with ARMA errors) by using the Econometric Modeler app. After you choose candidate models for estimation (see Perform Exploratory Data Analysis), you can specify the model structure of each. To do so, on the Econometric Modeler tab, in the Models section, click a model or display the gallery of supported models and click the model you want.

This is a screen shot of the Models drop-down with multiple options for ARMA/ARIMA, GARCH, and Regression models. There are buttons below the heading for each general category of model that correspond to specific supported model types.

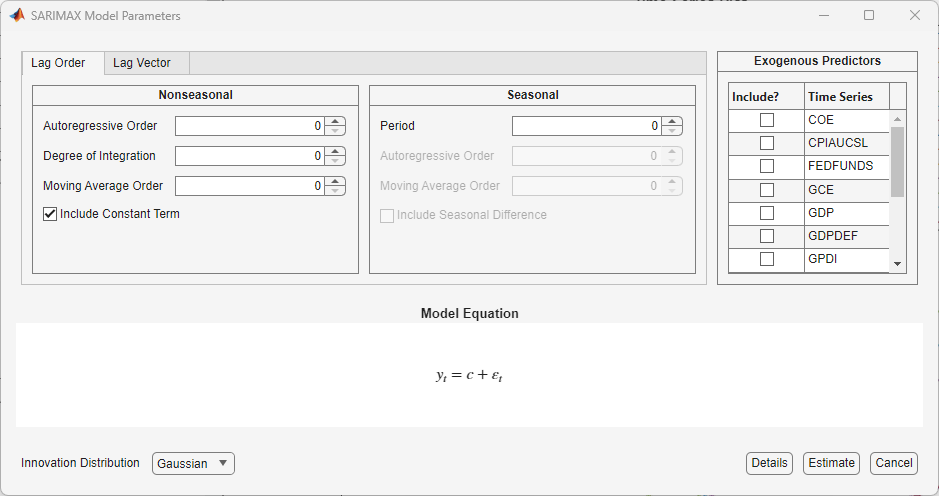
After you select a time series model, the Type Model Parameters dialog box appears, where Type is the model type. For example, if you select SARIMAX, then the SARIMAX Model Parameters dialog box appears.

SARIMAX Model Parameters dialog box showing parameter settings

For all dynamic models, Econometric Modeler supports two options to specify the lag operator polynomials. The adjustment options are on separate tabs: the Lag Order and Lag Vector tab. The Lag Order tab options offer a straight forward way to include consecutive lags from lag 1 and degrees of integration (see Specify Lag Structure Using Lag Order Tab). The Lag Vector tab options allow you to create flexible models (see Specify Lag Structure Using Lag Vector Tab).
The Type Model Parameters dialog box contains a Nonseasonal or Seasonal section. The Seasonal section is absent in strictly nonseasonal model dialog boxes. To specify the nonseasonal lag operator polynomial structure, use the parameters in the Nonseasonal section. To adjust the seasonal lag operator polynomial structure, including seasonality, use the parameters in the Seasonal section.
To specify the degrees of nonseasonal integration, in the Nonseasonal section, in the Degree of Integration box, type the degree, or click the appropriate arrow on .
To specify the seasonal periodicity for seasonal models, in the Seasonal section, in the Period box, type the periodicity, or click the appropriate arrow on . When the periodicity is greater than 0, you can specify the seasonal autoregressive or moving average polynomial order similarly, and you can specify one degree of seasonal integration by clicking the Include Seasonal Difference check box.
For verification, the model form appears in the Model Equation section. The model form updates to your specifications in real time.

Specify Lag Structure Using Lag Order Tab

On the Lag Order tab, in the Nonseasonal section, you can specify the orders of each lag operator polynomial in the nonseasonal component. In the appropriate lag polynomial order box (for example, the Autoregressive Order box), type the nonnegative integer order or click the appropriate arrow on . The app includes all consecutive lags from 1 through L in the polynomial, where L is the specified order.

For seasonal models, on the Lag Order tab, in the Seasonal section:

Specify the period in the season by entering the nonnegative integer period in the Period box or by clicking .
Specify the seasonal lag operator polynomial order. In the appropriate lag polynomial order box (for example, the Autoregressive Order box), type the nonnegative integer order ignoring seasonality or click . The lag operator exponents in the resulting polynomial are multiples of the specified period.

For example, if Period is 12 and Autoregressive Order in the Seasonal section is 3, then the seasonal autoregressive polynomial is $(1 - Φ_{4} L^{4} - Φ_{8} L^{8} - Φ_{12} L^{12})$ .

To specify seasonal integration, select the Include Seasonal Difference check box. A seasonal difference polynomial appears in the Model Equation section, and its lag operator exponent is equal to the specified period.

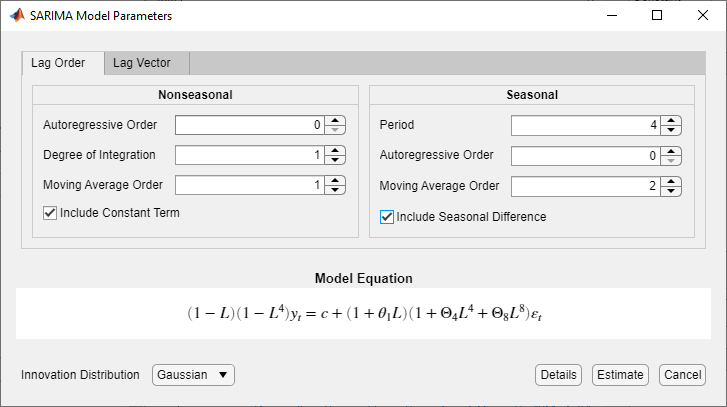
Consider a SARIMA(0,1,1)×(0,1,2)₄ model, a seasonal multiplicative ARIMA model with four periods in a season. To specify this model using the parameters in the Lag Order tab:

Select a time series variable in the Time Series pane.
On the Econometric Modeler tab, in the Models section, click the arrow > SARIMA.
In the SARIMA Model Parameters dialog box, on the Lag Order tab, enter these values for the corresponding parameters.
- In the Nonseasonal section, in the Degree of Integration box, type 1.
- In the Nonseasonal section, in the Moving Average Order box, type 1.
- In the Seasonal section, in the Period box, type 4. This value indicates a quarterly season.
- In the Seasonal section, in the Moving Average Order box, type 2. This action includes seasonal MA lags 4 and 8 in the equation.
- In the Seasonal section, select the Include Seasonal Difference check box.

SARIMA Model Parameters dialog box showing Lag Order tab with parameter settings

Specify Lag Structure Using Lag Vector Tab

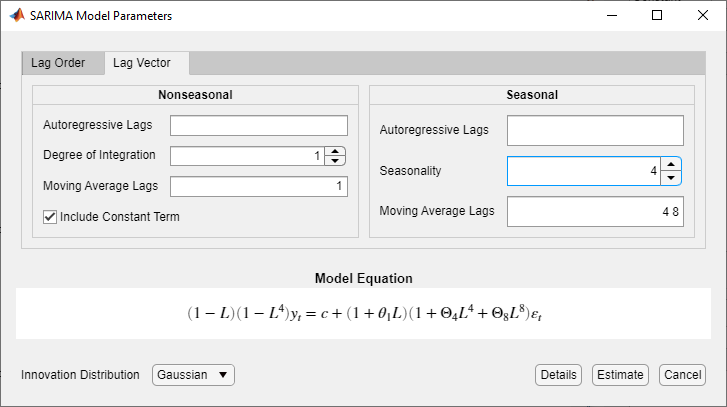
On the Lag Vector tab, you specify the lags in the corresponding seasonal or nonseasonal lag operator polynomial. This figure shows the Lag Vector tab in the SARIMA Model Parameters dialog box.

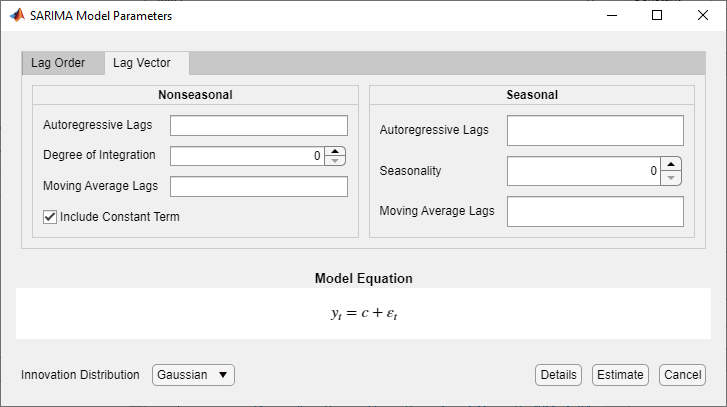
SARIMA Model Parameters dialog box showing Lag Vector tab with parameter settings

To specify the lags that comprise each lag operator polynomial, type a list of nonnegative, unique integers in the corresponding box. Separate values by commas or spaces, or use the colon operator (for example, 4:4:12).

Specify the seasonal-difference degree by typing a nonnegative integer in the Seasonality box or by clicking .

Consider a SARIMA(0,1,1)×(0,1,2)₄ model, a seasonal multiplicative ARIMA model with four periods in a season. To specify this model using the parameters in the Lag Vector tab:

Select a time series variable in the Time Series pane.
On the Econometric Modeler tab, in the Models section, click the arrow > SARIMA.
In the SARIMA Model Parameters dialog box, click the Lag Vector tab, then enter these values for the corresponding parameters.
- In the Nonseasonal section, in the Degree of Integration box, type 1.
- In the Nonseasonal section, in the Moving Average Lags box, type 1.
- In the Seasonal section, in the Seasonality box, type 4. Therefore, a seasonal-difference polynomial of degree 4 appears in the equation in the Model Equation section.
- In the Seasonal section, in the Moving Average Lags box, type 4 8. This action includes seasonal MA lags 4 and 8 in the equation.

SARIMA Model Parameters dialog box showing Lag Vector tab with parameter settings in the Nonseasonal and Seasonal sections