Main Content

Calibrate Shifted SABR Model Parameters for Swaption Instrument

Open Live Script

Calibrate model parameters for a Swaption instrument when you use a SABR pricing method.

Load Market Data

% Zero curve
ValuationDate = datetime("5-Mar-2016", 'Locale', 'en_US');
ZeroDates = datemnth(ValuationDate,[1 2 3 6 9 12*[1 2 3 4 5 6 7 8 9 10 12]])';
ZeroRates = [-0.33 -0.28 -0.24 -0.12 -0.08 -0.03 0.015 0.028 ...
    0.033 0.042 0.056 0.095 0.194 0.299 0.415 0.525]'/100;
Compounding = 1;
ZeroCurve = ratecurve("zero",ValuationDate,ZeroDates,ZeroRates,'Compounding',Compounding)
ZeroCurve = 
  ratecurve with properties:

                 Type: "zero"
          Compounding: 1
                Basis: 0
                Dates: [16x1 datetime]
                Rates: [16x1 double]
               Settle: 05-Mar-2016
         InterpMethod: "linear"
    ShortExtrapMethod: "next"
     LongExtrapMethod: "previous"


% Define the swaptions
SwaptionSettle = datetime("5-Mar-2016", 'Locale', 'en_US');
SwaptionExerciseDate = datetime("5-Mar-2017", 'Locale', 'en_US');
SwaptionStrikes = (-0.6:0.01:1.6)'/100; % Include negative strikes
SwapMaturity = datetime("5-Mar-2022", 'Locale', 'en_US'); % Maturity of underlying swap
OptSpec = 'call';

Compute Forward Swap Rate by Creating Swap Instrument

Use fininstrument to create a Swap instrument object. 

LegRate = [0 0];
Swap = fininstrument("Swap", 'Maturity', SwapMaturity, 'LegRate', LegRate, "LegType",["fixed" "float"],...
    "ProjectionCurve", ZeroCurve, "StartDate", SwaptionExerciseDate)
Swap = 
  Swap with properties:

                     LegRate: [0 0]
                     LegType: ["fixed"    "float"]
                       Reset: [2 2]
                       Basis: [0 0]
                    Notional: 100
          LatestFloatingRate: [NaN NaN]
                 ResetOffset: [0 0]
    DaycountAdjustedCashFlow: [0 0]
             ProjectionCurve: [1x2 ratecurve]
       BusinessDayConvention: ["actual"    "actual"]
                    Holidays: NaT
                EndMonthRule: [1 1]
                   StartDate: 05-Mar-2017
                    Maturity: 05-Mar-2022
                        Name: ""


ForwardValue = parswaprate(Swap,ZeroCurve)
ForwardValue = 
7.3271e-04

Load the Market Implied Volatility Data

The market swaption volatilities are quoted in terms of shifted Black volatilities with a 0.8 percent shift.

StrikeGrid = [-0.5; -0.25; -0.125; 0; 0.125; 0.25; 0.5; 1.0; 1.5]/100;
MarketStrikes = ForwardValue + StrikeGrid;
Shift = 0.008;  % 0.8 percent shift
MarketShiftedBlackVolatilities = [21.1; 15.3; 14.0; 14.6; 16.0; 17.7; 19.8; 23.9; 26.2]/100;
ATMShiftedBlackVolatility = MarketShiftedBlackVolatilities(StrikeGrid==0);

Calibrate Shifted SABR Model Parameters

The Beta parameter is predetermined at 0.5. Use volatilities to compute the implied volatility. 

Beta = 0.5;

% Calibrate Alpha, Rho, and Nu
objFun = @(X) MarketShiftedBlackVolatilities - volatilities(finpricer("Analytic", 'Model', ...
    finmodel("SABR", 'Alpha', X(1), 'Beta', Beta, 'Rho', X(2), 'Nu', X(3), 'Shift', Shift), ...
    'DiscountCurve', ZeroCurve), SwaptionExerciseDate, ForwardValue, MarketStrikes);

X = lsqnonlin(objFun, [0.5 0 0.5], [0 -1 0], [Inf 1 Inf]);
Local minimum possible.

lsqnonlin stopped because the final change in the sum of squares relative to 
its initial value is less than the value of the function tolerance.

Alpha = X(1);
Rho = X(2);
Nu = X(3);

Create SABR Model Using the Calibrated Parameters

Use finmodel to create a SABR model object.

SABRModel = finmodel("SABR",'Alpha',Alpha,'Beta',Beta,'Rho',Rho,'Nu',Nu,'Shift',Shift)
SABRModel = 
  SABR with properties:

             Alpha: 0.0135
              Beta: 0.5000
               Rho: 0.4654
                Nu: 0.4957
             Shift: 0.0080
    VolatilityType: "black"

Create SABR Pricer Using Calibrated SABR Model and Compute Volatilities

Use finpricer to create a SABR pricer object and use the ratecurve object for the 'DiscountCurve' name-value pair argument.

SABRPricer = finpricer("Analytic", 'Model', SABRModel, 'DiscountCurve', ZeroCurve)
SABRPricer = 
  SABR with properties:

    DiscountCurve: [1x1 ratecurve]
            Model: [1x1 finmodel.SABR]


SABRShiftedBlackVolatilities = volatilities(SABRPricer, SwaptionExerciseDate, ForwardValue, SwaptionStrikes)
SABRShiftedBlackVolatilities = 221×1

    0.2978
    0.2911
    0.2848
    0.2787
    0.2729
    0.2673
    0.2620
    0.2568
    0.2518
    0.2470
      ⋮


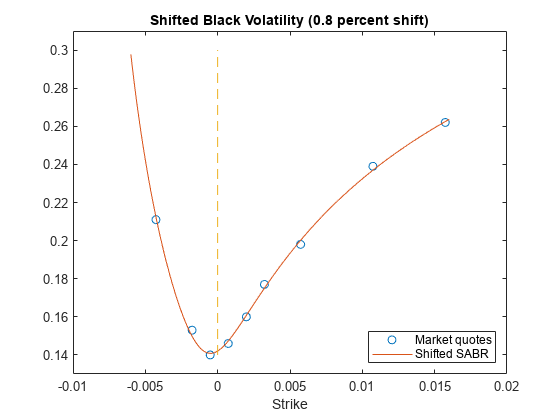
figure;
plot(MarketStrikes, MarketShiftedBlackVolatilities, 'o', ...
    SwaptionStrikes, SABRShiftedBlackVolatilities);
h = gca;
line([0,0],[min(h.YLim),max(h.YLim)],'LineStyle','--');
ylim([0.13 0.31])
xlabel('Strike');
legend('Market quotes','Shifted SABR', 'location', 'southeast');
title (['Shifted Black Volatility (',num2str(Shift*100),' percent shift)']);

Figure contains an axes object. The axes object with title Shifted Black Volatility (0.8 percent shift), xlabel Strike contains 3 objects of type line. One or more of the lines displays its values using only markers These objects represent Market quotes, Shifted SABR.

Price Swaption Instruments Using Calibrated SABR Model and SABR Pricer

% Create swaption instruments
NumInst = length(SwaptionStrikes);
Swaptions(NumInst, 1) = fininstrument("Swaption", ...
    'Strike', SwaptionStrikes(1), 'ExerciseDate', SwaptionExerciseDate(1), 'Swap', Swap);
for k = 1:NumInst
    Swaptions(k) = fininstrument("Swaption", 'Strike', SwaptionStrikes(k), ...
        'ExerciseDate', SwaptionExerciseDate, 'Swap', Swap, 'OptionType', OptSpec);
end
Swaptions
Swaptions=221×1 Swaption array with properties:
    OptionType
    ExerciseStyle
    ExerciseDate
    Strike
    Swap
    Name
      ⋮


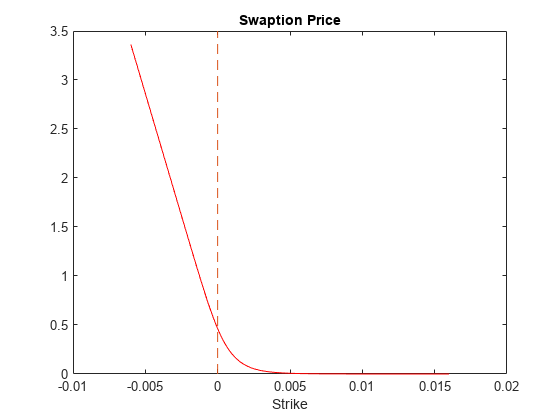
% Price swaptions using the SABR pricer
SwaptionPrices = price(SABRPricer,Swaptions);

figure;
plot(SwaptionStrikes, SwaptionPrices, 'r');
h = gca;
line([0,0],[min(h.YLim),max(h.YLim)],'LineStyle','--');
xlabel('Strike');
title ('Swaption Price');

Figure contains an axes object. The axes object with title Swaption Price, xlabel Strike contains 2 objects of type line.