Swaption
Swaption instrument object
Description
Create and price a Swaption instrument object for one or
more Swaption instruments using this workflow:
Use
fininstrumentto create aSwaptioninstrument object for one or more Swaption instruments.Use
finmodelto specify aHullWhite,BlackKarasinski,BlackDermanToy,Black,Normal,SABR,CoxIngersollRoss, orLinearGaussian2Fmodel for theSwaptioninstrument object.Choose a pricing method.
When using a
HullWhite,BlackKarasinski,BlackDermanToy,CoxIngersollRoss,Black,Normal, orSABRmodel, usefinpricerfor pricing one or moreSwaptioninstruments and specify:When using a
HullWhite,BlackKarasinski, orLinearGaussian2Fmodel, usefinpricerto specify anIRMonteCarlopricing method for one or moreSwaptioninstruments.
For more information on this workflow, see Get Started with Workflows Using Object-Based Framework for Pricing Financial Instruments.
For more information on the available models and pricing methods for a
Swaption instrument, see Choose Instruments, Models, and Pricers.
Creation
Syntax
Description
SwaptionInstrument = fininstrument(InstrumentType,'Strike',strike_value,'ExerciseDate',exercice_date)Swaption object for one or more Swaption
instruments by specifying InstrumentType and sets the
properties for the
required name-value pair arguments Strike and
ExerciseDate. For more information on a
Swaption instrument, see More About.
SwaptionInstrument = fininstrument(___,Name,Value)SwaptionInstrument =
fininstrument("Swaption",'Strike',0.67,'ExerciseDate',datetime(2019,1,30),'Swap',Swap_obj,'OptionType',"put",'ExerciseStyle',"European",'Name',"swaption_instrument")
creates a Swaption put instrument with a strike of 0.67
and an European exercise. You can specify multiple name-value pair
arguments.
Input Arguments
Instrument type, specified as a string with the value of
"Swaption", a character vector with the value of
'Swaption', an
NINST-by-1 string array with
values of "Swaption", or an
NINST-by-1 cell array of
character vectors with values of 'Swaption'.
Data Types: char | cell | string
Name-Value Arguments
Specify required
and optional pairs of arguments as
Name1=Value1,...,NameN=ValueN, where
Name is the argument name and Value is
the corresponding value. Name-value arguments must appear after other arguments,
but the order of the pairs does not matter.
Before R2021a, use commas to separate each name and value, and enclose
Name in quotes.
Example: SwaptionInstrument =
fininstrument("Swaption",'Strike',.67,'ExerciseDate',datetime(2019,1,30),'Swap',Swap_obj,'OptionType',"put",'ExerciseStyle',"European",'Name',"swaption_instrument")
Required Swaption Name-Value Pair Arguments
Option strike value, specified as the comma-separated pair
consisting of 'Strike' and a scalar nonnegative
decimal or an NINST-by-1
vector of nonnegative decimals.
Data Types: double
Option exercise date, specified as the comma-separated pair
consisting of 'ExerciseDate' and a scalar or an
NINST-by-1 vector using a
datetime array, string array,or date character vectors.
Note
For a European option, there is only one
ExerciseDate on the option expiry
date.
To support existing code, Swaption also
accepts serial date numbers as inputs, but they are not recommended.
If you use date character vectors or strings, the format must be
recognizable by datetime because
the ExerciseDate property is stored as a
datetime.
Underlying Swap object, specified as the
comma-separated pair consisting of 'Swap' and a
scalar Swap
object or an NINST-by-1 vector
of Swap objects.
Data Types: object
Optional Swaption Name-Value Pair Arguments
Option type, specified as the comma-separated pair consisting of
'OptionType' and a scalar string or character
vector or an NINST-by-1 cell
array of character vectors or string array.
Data Types: char | cell | string
Option exercise style, specified as the comma-separated pair
consisting of 'ExerciseStyle' and a scalar string
or character vector or an
NINST-by-1 cell array of
character vectors or string array.
Note
When you specify a Swap instrument as the underlying asset for a
Swaption instrument and use a Normal, SABR, Black, or HullWhite pricer, the Swap instrument LegType
must be ["fixed","float"] or
["float","fixed"] and the
Swaption instrument
ExerciseStyle must be
"European".
Data Types: string | cell | char
User-defined name for the instrument, specified as the
comma-separated pair consisting of 'Name' and a
scalar string or character vector or an
NINST-by-1 cell array of
character vectors or string array.
Data Types: char | cell | string
Output Arguments
Swaption instrument, returned as a Swaption
object.
Properties
Option strike value, returned as a scalar nonnegative decimal or an
NINST-by-1 vector of nonnegative
decimals.
Data Types: double
Option exercise date, returned as a scalar datetime or an
NINST-by-1 vector of
datetimes.
Data Types: datetime
Swap object, returned as a scalar Swap object or
an NINST-by-1 vector of
Swap objects.
Data Types: object
Option type, returned as a scalar string or an
NINST-by-1 string array with a
value of "call" or "put".
Data Types: string
Option exercise style, returned as a scalar string or an
NINST-by-1 string array with a
value of "European".
Data Types: string
User-defined name for the instrument, returned as a string or an
NINST-by-1 string array.
Data Types: string
Examples
This example shows the workflow to price a Swaption instrument when you use a SABR model and a SABR pricing method.
Create ratecurve Object
Create a ratecurve object using ratecurve.
Settle = datetime(2018,9,15); Type = 'zero'; ZeroTimes = [calmonths(6) calyears([1 2 3 4 5 7 10 20 30])]'; ZeroRates = [0.0052 0.0055 0.0061 0.0073 0.0094 0.0119 0.0168 0.0222 0.0293 0.0307]'; ZeroDates = Settle + ZeroTimes; myRC = ratecurve('zero',Settle,ZeroDates,ZeroRates)
myRC =
ratecurve with properties:
Type: "zero"
Compounding: -1
Basis: 0
Dates: [10×1 datetime]
Rates: [10×1 double]
Settle: 15-Sep-2018
InterpMethod: "linear"
ShortExtrapMethod: "next"
LongExtrapMethod: "previous"
Create Swap Instrument Object
Use fininstrument to create the underlying Swap instrument object.
Swap = fininstrument("Swap",'Maturity',datetime(2027,3,15),'LegRate',[0 0],'LegType',... ["float","fixed"],'Notional',100,'StartDate',datetime(2022,3,15),'Name',"swap_instrument")
Swap =
Swap with properties:
LegRate: [0 0]
LegType: ["float" "fixed"]
Reset: [2 2]
Basis: [0 0]
Notional: 100
LatestFloatingRate: [NaN NaN]
ResetOffset: [0 0]
DaycountAdjustedCashFlow: [0 0]
ProjectionCurve: [0×0 ratecurve]
BusinessDayConvention: ["actual" "actual"]
Holidays: NaT
EndMonthRule: [1 1]
StartDate: 15-Mar-2022
Maturity: 15-Mar-2027
Name: "swap_instrument"
Create Swaption Instrument Object
Use fininstrument to create a Swaption instrument object.
Swaption = fininstrument("Swaption",'Strike',0.02,'ExerciseDate',datetime(2022,3,15),'Swap',Swap,'Name',"swaption_option")
Swaption =
Swaption with properties:
OptionType: "call"
ExerciseStyle: "european"
ExerciseDate: 15-Mar-2022
Strike: 0.0200
Swap: [1×1 fininstrument.Swap]
Name: "swaption_option"
Create SABR Model Object
Use finmodel to create a SABR model object.
SabrModel = finmodel("SABR",'Alpha',0.032,'Beta',0.04,'Rho',.08,'Nu',0.49,'Shift',0.002)
SabrModel =
SABR with properties:
Alpha: 0.0320
Beta: 0.0400
Rho: 0.0800
Nu: 0.4900
Shift: 0.0020
VolatilityType: "black"
Create SABR Pricer Object
Use finpricer to create a SABR pricer object and use the ratecurve object for the 'DiscountCurve' name-value pair argument.
outPricer = finpricer("analytic",'Model',SabrModel,'DiscountCurve',myRC)
outPricer =
SABR with properties:
DiscountCurve: [1×1 ratecurve]
Model: [1×1 finmodel.SABR]
Price Swaption Instrument
Use price to compute the price for the Swaption instrument.
Price = price(outPricer,Swaption)
Price = 10.8558
This example shows the workflow to price multiple Swaption instrument when you use a SABR model and a SABR pricing method.
Create ratecurve Object
Create a ratecurve object using ratecurve.
Settle = datetime(2018,9,15); Type = 'zero'; ZeroTimes = [calmonths(6) calyears([1 2 3 4 5 7 10 20 30])]'; ZeroRates = [0.0052 0.0055 0.0061 0.0073 0.0094 0.0119 0.0168 0.0222 0.0293 0.0307]'; ZeroDates = Settle + ZeroTimes; myRC = ratecurve('zero',Settle,ZeroDates,ZeroRates)
myRC =
ratecurve with properties:
Type: "zero"
Compounding: -1
Basis: 0
Dates: [10×1 datetime]
Rates: [10×1 double]
Settle: 15-Sep-2018
InterpMethod: "linear"
ShortExtrapMethod: "next"
LongExtrapMethod: "previous"
Create Swap Instrument Object
Use fininstrument to create the underlying Swap instrument object.
Swap = fininstrument("Swap",'Maturity',datetime(2027,3,15),'LegRate',[0 0],'LegType',... ["float","fixed"],'Notional',100,'StartDate',datetime(2022,3,15),'Name',"swap_instrument")
Swap =
Swap with properties:
LegRate: [0 0]
LegType: ["float" "fixed"]
Reset: [2 2]
Basis: [0 0]
Notional: 100
LatestFloatingRate: [NaN NaN]
ResetOffset: [0 0]
DaycountAdjustedCashFlow: [0 0]
ProjectionCurve: [0×0 ratecurve]
BusinessDayConvention: ["actual" "actual"]
Holidays: NaT
EndMonthRule: [1 1]
StartDate: 15-Mar-2022
Maturity: 15-Mar-2027
Name: "swap_instrument"
Create Swaption Instrument Object
Use fininstrument to create a Swaption instrument object for three Swaption instruments.
Swaption = fininstrument("Swaption",'Strike',[0.02 ; 0.03 ; 0.04],'ExerciseDate',datetime([2022,3,15 ; 2022,4,15 ; 2022,5,15]),'Swap',Swap,'Name',"swaption_option")
Swaption=3×1 Swaption array with properties:
OptionType
ExerciseStyle
ExerciseDate
Strike
Swap
Name
Create SABR Model Object
Use finmodel to create a SABR model object.
SabrModel = finmodel("SABR",'Alpha',0.032,'Beta',0.04,'Rho',.08,'Nu',0.49,'Shift',0.002)
SabrModel =
SABR with properties:
Alpha: 0.0320
Beta: 0.0400
Rho: 0.0800
Nu: 0.4900
Shift: 0.0020
VolatilityType: "black"
Create SABR Pricer Object
Use finpricer to create a SABR pricer object and use the ratecurve object for the 'DiscountCurve' name-value pair argument.
outPricer = finpricer("analytic",'Model',SabrModel,'DiscountCurve',myRC)
outPricer =
SABR with properties:
DiscountCurve: [1×1 ratecurve]
Model: [1×1 finmodel.SABR]
Price Swaption Instruments
Use price to compute the prices for the Swaption instruments.
Price = price(outPricer,Swaption)
Price = 3×1
10.8558
9.0442
7.4883
This example shows the workflow to price a Swaption instrument when you use a Black model and a Black pricing method.
Create ratecurve Object
Create a ratecurve object using ratecurve.
Settle = datetime(2018,9,15); Type = 'zero'; ZeroTimes = [calmonths(6) calyears([1 2 3 4 5 7 10 20 30])]'; ZeroRates = [0.0052 0.0055 0.0061 0.0073 0.0094 0.0119 0.0168 0.0222 0.0293 0.0307]'; ZeroDates = Settle + ZeroTimes; myRC = ratecurve('zero',Settle,ZeroDates,ZeroRates)
myRC =
ratecurve with properties:
Type: "zero"
Compounding: -1
Basis: 0
Dates: [10×1 datetime]
Rates: [10×1 double]
Settle: 15-Sep-2018
InterpMethod: "linear"
ShortExtrapMethod: "next"
LongExtrapMethod: "previous"
Create Swap Instrument Object
Use fininstrument to create the underlying Swap instrument object.
Swap = fininstrument("Swap",'Maturity',datetime(2027,3,15),'LegRate',[0 0],'LegType',... ["float","fixed"],'Notional',100,'StartDate',datetime(2022,3,15),'Name',"swap_instrument")
Swap =
Swap with properties:
LegRate: [0 0]
LegType: ["float" "fixed"]
Reset: [2 2]
Basis: [0 0]
Notional: 100
LatestFloatingRate: [NaN NaN]
ResetOffset: [0 0]
DaycountAdjustedCashFlow: [0 0]
ProjectionCurve: [0×0 ratecurve]
BusinessDayConvention: ["actual" "actual"]
Holidays: NaT
EndMonthRule: [1 1]
StartDate: 15-Mar-2022
Maturity: 15-Mar-2027
Name: "swap_instrument"
Create Swaption Instrument Object
Use fininstrument to create a Swaption instrument object.
Swaption = fininstrument("Swaption",'Strike',0.02,'ExerciseDate',datetime(2022,3,15),'Swap',Swap,'Name',"swaption_option")
Swaption =
Swaption with properties:
OptionType: "call"
ExerciseStyle: "european"
ExerciseDate: 15-Mar-2022
Strike: 0.0200
Swap: [1×1 fininstrument.Swap]
Name: "swaption_option"
Create Black Model Object
Use finmodel to create a Black model object.
BlackModel = finmodel("Black",'Volatility',0.032,'Shift',0.002)
BlackModel =
Black with properties:
Volatility: 0.0320
Shift: 0.0020
Create Black Pricer Object
Use finpricer to create a Black pricer object and use the ratecurve object for the 'DiscountCurve' name-value pair argument.
outPricer = finpricer("analytic",'Model',BlackModel,'DiscountCurve',myRC)
outPricer =
Black with properties:
Model: [1×1 finmodel.Black]
DiscountCurve: [1×1 ratecurve]
Price Swaption Instrument
Use price to compute the price for the Swaption instrument.
Price = price(outPricer,Swaption)
Price = 3.3116
This example shows the workflow to price a Swaption instrument when you use a HullWhite model and an IRTree pricing method.
Create ratecurve Object
Create a ratecurve object using ratecurve.
Settle = datetime(2018,9,15); Type = 'zero'; ZeroTimes = [calmonths(6) calyears([1 2 3 4 5 7 10 20 30])]'; ZeroRates = [0.0052 0.0055 0.0061 0.0073 0.0094 0.0119 0.0168 0.0222 0.0293 0.0307]'; ZeroDates = Settle + ZeroTimes; myRC = ratecurve('zero',Settle,ZeroDates,ZeroRates)
myRC =
ratecurve with properties:
Type: "zero"
Compounding: -1
Basis: 0
Dates: [10×1 datetime]
Rates: [10×1 double]
Settle: 15-Sep-2018
InterpMethod: "linear"
ShortExtrapMethod: "next"
LongExtrapMethod: "previous"
Create Swap Instrument Object
Use fininstrument to create the underlying Swap instrument object.
Swap = fininstrument("Swap",'Maturity',datetime(2027,3,15),'LegRate',[0 0],'LegType',... ["float","fixed"],'Notional',100,'StartDate',datetime(2022,3,15),'Name',"swap_instrument")
Swap =
Swap with properties:
LegRate: [0 0]
LegType: ["float" "fixed"]
Reset: [2 2]
Basis: [0 0]
Notional: 100
LatestFloatingRate: [NaN NaN]
ResetOffset: [0 0]
DaycountAdjustedCashFlow: [0 0]
ProjectionCurve: [0×0 ratecurve]
BusinessDayConvention: ["actual" "actual"]
Holidays: NaT
EndMonthRule: [1 1]
StartDate: 15-Mar-2022
Maturity: 15-Mar-2027
Name: "swap_instrument"
Create Swaption Instrument Object
Use fininstrument to create a Swaption instrument object.
Swaption = fininstrument("Swaption",'Strike',0.02,'ExerciseDate',datetime(2022,3,15),'Swap',Swap,'Name',"swaption_option")
Swaption =
Swaption with properties:
OptionType: "call"
ExerciseStyle: "european"
ExerciseDate: 15-Mar-2022
Strike: 0.0200
Swap: [1×1 fininstrument.Swap]
Name: "swaption_option"
Create HullWhite Model Object
Use finmodel to create a HullWhite model object.
HullWhiteModel = finmodel("HullWhite",'Alpha',0.032,'Sigma',0.04)
HullWhiteModel =
HullWhite with properties:
Alpha: 0.0320
Sigma: 0.0400
Create IRTree Pricer Object
Use finpricer to create an IRTree pricer object and use the ratecurve object for the 'DiscountCurve' name-value pair argument.
outPricer = finpricer("IRTree",'Model',HullWhiteModel,'DiscountCurve',myRC,'TreeDates',ZeroDates)
outPricer =
HWBKTree with properties:
Tree: [1×1 struct]
TreeDates: [10×1 datetime]
Model: [1×1 finmodel.HullWhite]
DiscountCurve: [1×1 ratecurve]
Price Swaption Instrument
Use price to compute the price and sensitivities for the Swaption instrument.
[Price, outPR] = price(outPricer,Swaption,["all"])Price = 14.6783
outPR =
priceresult with properties:
Results: [1×4 table]
PricerData: [1×1 struct]
outPR.Results
ans=1×4 table
Price Delta Gamma Vega
______ ______ _______ _____
14.678 142.29 -2263.2 321.8
This example shows the workflow to price a Swaption instrument when using a LinearGaussian2F model and an IRMonteCarlo pricing method.
Create ratecurve Object
Create a ratecurve object using ratecurve.
Settle = datetime(2019,1,1); Type = 'zero'; ZeroTimes = [calmonths(6) calyears([1 2 3 4 5 7 10 20 30])]'; ZeroRates = [0.0052 0.0055 0.0061 0.0073 0.0094 0.0119 0.0168 0.0222 0.0293 0.0307]'; ZeroDates = Settle + ZeroTimes; myRC = ratecurve('zero',Settle,ZeroDates,ZeroRates)
myRC =
ratecurve with properties:
Type: "zero"
Compounding: -1
Basis: 0
Dates: [10×1 datetime]
Rates: [10×1 double]
Settle: 01-Jan-2019
InterpMethod: "linear"
ShortExtrapMethod: "next"
LongExtrapMethod: "previous"
Create Swap Instrument Object
Use fininstrument to create the underlying Swap instrument object.
Swap = fininstrument("Swap",'Maturity',datetime(2022,1,1),'LegRate',[0.05,0.04],'Name',"swap_instrument")
Swap =
Swap with properties:
LegRate: [0.0500 0.0400]
LegType: ["fixed" "float"]
Reset: [2 2]
Basis: [0 0]
Notional: 100
LatestFloatingRate: [NaN NaN]
ResetOffset: [0 0]
DaycountAdjustedCashFlow: [0 0]
ProjectionCurve: [0×0 ratecurve]
BusinessDayConvention: ["actual" "actual"]
Holidays: NaT
EndMonthRule: [1 1]
StartDate: NaT
Maturity: 01-Jan-2022
Name: "swap_instrument"
Create Swaption Instrument Object
Use fininstrument to create a Swaption instrument object.
Swaption = fininstrument("Swaption",'Strike',0.02,'ExerciseDate',datetime(2021,7,1),'Swap',Swap,'Name',"swaption_option")
Swaption =
Swaption with properties:
OptionType: "call"
ExerciseStyle: "european"
ExerciseDate: 01-Jul-2021
Strike: 0.0200
Swap: [1×1 fininstrument.Swap]
Name: "swaption_option"
Create LinearGaussian2F Model Object
Use finmodel to create a LinearGaussian2F model object.
LinearGaussian2FModel = finmodel("LinearGaussian2F",'Alpha1',0.07,'Sigma1',0.01,'Alpha2',0.5,'Sigma2',0.006,'Correlation',-0.7)
LinearGaussian2FModel =
LinearGaussian2F with properties:
Alpha1: 0.0700
Sigma1: 0.0100
Alpha2: 0.5000
Sigma2: 0.0060
Correlation: -0.7000
Create IRMonteCarlo Pricer Object
Use finpricer to create an IRMonteCarlo pricer object and use the ratecurve object for the 'DiscountCurve' name-value pair argument.
simDates = datetime(2019,7,1)+calmonths(0:6:30); outPricer = finpricer("IRMonteCarlo",'Model',LinearGaussian2FModel,'DiscountCurve',myRC,'SimulationDates',simDates)
outPricer =
G2PPMonteCarlo with properties:
NumTrials: 1000
RandomNumbers: []
DiscountCurve: [1×1 ratecurve]
SimulationDates: [01-Jul-2019 01-Jan-2020 01-Jul-2020 01-Jan-2021 01-Jul-2021 01-Jan-2022]
Model: [1×1 finmodel.LinearGaussian2F]
Price Swaption Instrument
Use price to compute the price and sensitivities for the Swaption instrument.
[Price,outPR] = price(outPricer,Swaption,["all"])Price = 1.5065
outPR =
priceresult with properties:
Results: [1×4 table]
PricerData: [1×1 struct]
outPR.Results
ans=1×4 table
Price Delta Gamma Vega
______ ______ ______ _________________
1.5065 44.746 -257.2 1.6729 -2.0015
This example shows the workflow to price a Swaption instrument when you use a CoxIngersollRoss model and an IRTree pricing method.
Create ratecurve Object
Create a ratecurve object using ratecurve.
Times= [calyears([1 2 3 4 ])]';
Settle = datetime(2023,1,1);
ZRates = [0.035; 0.042147; 0.047345; 0.052707]';
ZDates = Settle + Times;
Compounding = -1;
Basis = 1;
ZeroCurve = ratecurve("zero",Settle,ZDates,ZRates,Compounding = Compounding, Basis = Basis);Create Swap Instrument Object
Use fininstrument to first create a Swap instrument object.
Maturity = datetime(2027,1,1); LegType = ["fixed","float"]; LegRate = [0.06 0.0020]; Reset = 1; Swap = fininstrument("Swap",Maturity=Maturity,LegRate=LegRate,LegType=LegType,Reset=[Reset Reset],Name="Swap_inst")
Swap =
Swap with properties:
LegRate: [0.0600 0.0020]
LegType: ["fixed" "float"]
Reset: [1 1]
Basis: [0 0]
Notional: 100
LatestFloatingRate: [NaN NaN]
ResetOffset: [0 0]
DaycountAdjustedCashFlow: [0 0]
ProjectionCurve: [0×0 ratecurve]
BusinessDayConvention: ["actual" "actual"]
Holidays: NaT
EndMonthRule: [1 1]
StartDate: NaT
Maturity: 01-Jan-2027
Name: "Swap_inst"
Create Swaption Instrument Object
Use fininstrument to first create a Swaption instrument object.
Maturity = datetime(2027,1,1); ExerciseDate = datetime(2026,1,1); Strike = parswaprate(Swap,ZeroCurve); OptionType = 'call'; Swaption = fininstrument("Swaption",ExerciseDate=ExerciseDate,Strike=Strike,Swap=Swap,OptionType=OptionType,Name="Swaption_inst")
Swaption =
Swaption with properties:
OptionType: "call"
ExerciseStyle: "european"
ExerciseDate: 01-Jan-2026
Strike: 0.0554
Swap: [1×1 fininstrument.Swap]
Name: "Swaption_inst"
Create CoxIngersollRoss Model Object
Then use finmodel to create a CoxIngersollRoss model object.
alpha = 0.03;
theta = 0.02;
sigma = 0.1;
CIRModel = finmodel("CoxIngersollRoss",Sigma=sigma,Alpha=alpha,Theta=theta)CIRModel =
CoxIngersollRoss with properties:
Sigma: 0.1000
Alpha: 0.0300
Theta: 0.0200
Create IRTree Pricer Object
Use finpricer to create an IRTree pricer object for the CoxIngersollRoss model and use the ratecurve object for the 'DiscountCurve' name-value argument.
CIRPricer = finpricer("irtree",Model=CIRModel,DiscountCurve=ZeroCurve,Maturity=ZDates(end),NumPeriods=length(ZDates))CIRPricer =
CIRTree with properties:
Tree: [1×1 struct]
TreeDates: [4×1 datetime]
Model: [1×1 finmodel.CoxIngersollRoss]
DiscountCurve: [1×1 ratecurve]
Price Swaption Instrument
Use price to compute the price for the Swaption instrument.
[Price,outPR] = price(CIRPricer,Swaption,"all")Price = 1.6356
outPR =
priceresult with properties:
Results: [1×4 table]
PricerData: [1×1 struct]
outPR.Results
ans=1×4 table
Price Delta Gamma Vega
______ ______ _______ ______
1.6356 54.752 -281.84 5.9963
Calibrate model parameters for a Swaption instrument when you use a SABR pricing method.
Load Market Data
% Zero curve ValuationDate = datetime("5-Mar-2016", 'Locale', 'en_US'); ZeroDates = datemnth(ValuationDate,[1 2 3 6 9 12*[1 2 3 4 5 6 7 8 9 10 12]])'; ZeroRates = [-0.33 -0.28 -0.24 -0.12 -0.08 -0.03 0.015 0.028 ... 0.033 0.042 0.056 0.095 0.194 0.299 0.415 0.525]'/100; Compounding = 1; ZeroCurve = ratecurve("zero",ValuationDate,ZeroDates,ZeroRates,'Compounding',Compounding)
ZeroCurve =
ratecurve with properties:
Type: "zero"
Compounding: 1
Basis: 0
Dates: [16×1 datetime]
Rates: [16×1 double]
Settle: 05-Mar-2016
InterpMethod: "linear"
ShortExtrapMethod: "next"
LongExtrapMethod: "previous"
% Define the swaptions. SwaptionSettle = datetime("5-Mar-2016", 'Locale', 'en_US'); SwaptionExerciseDate = datetime("5-Mar-2017", 'Locale', 'en_US'); SwaptionStrikes = (-0.6:0.01:1.6)'/100; % Include negative strikes SwapMaturity = datetime("5-Mar-2022", 'Locale', 'en_US'); % Maturity of underlying swap OptSpec = 'call';
Compute Forward Swap Rate by Creating Swap Instrument
Use fininstrument to create a Swap instrument object.
LegRate = [0 0]; Swap = fininstrument("Swap", 'Maturity', SwapMaturity, 'LegRate', LegRate, "LegType",["fixed" "float"], ... "ProjectionCurve", ZeroCurve, "StartDate", SwaptionExerciseDate)
Swap =
Swap with properties:
LegRate: [0 0]
LegType: ["fixed" "float"]
Reset: [2 2]
Basis: [0 0]
Notional: 100
LatestFloatingRate: [NaN NaN]
ResetOffset: [0 0]
DaycountAdjustedCashFlow: [0 0]
ProjectionCurve: [1×2 ratecurve]
BusinessDayConvention: ["actual" "actual"]
Holidays: NaT
EndMonthRule: [1 1]
StartDate: 05-Mar-2017
Maturity: 05-Mar-2022
Name: ""
ForwardValue = parswaprate(Swap,ZeroCurve)
ForwardValue = 7.3271e-04
Load the Market Implied Volatility Data
The market swaption volatilities are quoted in terms of shifted Black volatilities with a 0.8 percent shift.
StrikeGrid = [-0.5; -0.25; -0.125; 0; 0.125; 0.25; 0.5; 1.0; 1.5]/100;
MarketStrikes = ForwardValue + StrikeGrid;
Shift = 0.008; % 0.8 percent shift
MarketShiftedBlackVolatilities = [21.1; 15.3; 14.0; 14.6; 16.0; 17.7; 19.8; 23.9; 26.2]/100;
ATMShiftedBlackVolatility = MarketShiftedBlackVolatilities(StrikeGrid==0);Calibrate Shifted SABR Model Parameters
The Beta parameter is predetermined at 0.5. Use volatilities to compute the implied volatility.
Beta = 0.5; % Calibrate Alpha, Rho, and Nu objFun = @(X) MarketShiftedBlackVolatilities - volatilities(finpricer("Analytic", 'Model', ... finmodel("SABR", 'Alpha', X(1), 'Beta', Beta, 'Rho', X(2), 'Nu', X(3), 'Shift', Shift), ... 'DiscountCurve', ZeroCurve), SwaptionExerciseDate, ForwardValue, MarketStrikes); X = lsqnonlin(objFun, [0.5 0 0.5], [0 -1 0], [Inf 1 Inf]);
Local minimum possible. lsqnonlin stopped because the final change in the sum of squares relative to its initial value is less than the value of the function tolerance. <stopping criteria details>
Alpha = X(1); Rho = X(2); Nu = X(3);
Create SABR Model Using the Calibrated Parameters
Use finmodel to create a SABR model object.
SABRModel = finmodel("SABR",'Alpha',Alpha,'Beta',Beta,'Rho',Rho,'Nu',Nu,'Shift',Shift)
SABRModel =
SABR with properties:
Alpha: 0.0135
Beta: 0.5000
Rho: 0.4654
Nu: 0.4957
Shift: 0.0080
VolatilityType: "black"
Create SABR Pricer Using Calibrated SABR Model and Compute Volatilities
Use finpricer to create a SABR pricer object and use the ratecurve object for the 'DiscountCurve' name-value pair argument.
SABRPricer = finpricer("Analytic", 'Model', SABRModel, 'DiscountCurve', ZeroCurve)
SABRPricer =
SABR with properties:
DiscountCurve: [1×1 ratecurve]
Model: [1×1 finmodel.SABR]
SABRShiftedBlackVolatilities = volatilities(SABRPricer, SwaptionExerciseDate, ForwardValue, SwaptionStrikes)
SABRShiftedBlackVolatilities = 221×1
0.2978
0.2911
0.2848
0.2787
0.2729
0.2673
0.2620
0.2568
0.2518
0.2470
0.2423
0.2378
0.2335
0.2293
0.2252
⋮
figure; plot(MarketStrikes, MarketShiftedBlackVolatilities, 'o', ... SwaptionStrikes, SABRShiftedBlackVolatilities); h = gca; line([0,0],[min(h.YLim),max(h.YLim)],'LineStyle','--'); ylim([0.13 0.31]) xlabel('Strike'); legend('Market quotes','Shifted SABR', 'location', 'southeast'); title (['Shifted Black Volatility (',num2str(Shift*100),' percent shift)']);
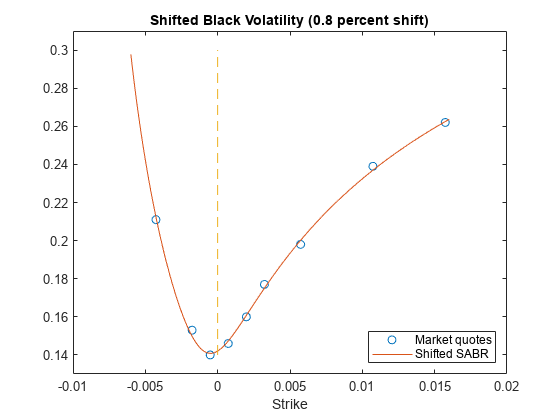
Price Swaption Instruments Using Calibrated SABR Model and SABR Pricer
% Create swaption instruments. NumInst = length(SwaptionStrikes); Swaptions(NumInst, 1) = fininstrument("Swaption", ... 'Strike', SwaptionStrikes(1), 'ExerciseDate', SwaptionExerciseDate(1), 'Swap', Swap); for k = 1:NumInst Swaptions(k) = fininstrument("Swaption", 'Strike', SwaptionStrikes(k), ... 'ExerciseDate', SwaptionExerciseDate, 'Swap', Swap, 'OptionType', OptSpec); end Swaptions
Swaptions=221×1 Swaption array with properties:
OptionType
ExerciseStyle
ExerciseDate
Strike
Swap
Name
⋮
% Price swaptions using the SABR pricer. SwaptionPrices = price(SABRPricer,Swaptions); figure; plot(SwaptionStrikes, SwaptionPrices, 'r'); h = gca; line([0,0],[min(h.YLim),max(h.YLim)],'LineStyle','--'); xlabel('Strike'); title ('Swaption Price');
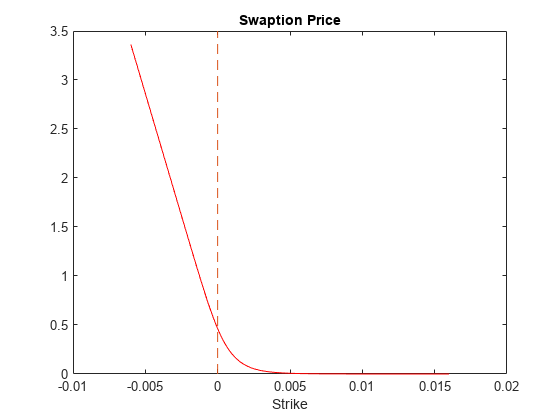
More About
A swaption (swap option) is a financial derivative that gives the holder the right, but not the obligation, to enter into an interest-rate swap agreement at a specified future date and under predetermined terms.
Swaptions are used by investors and institutions to hedge against interest rate fluctuations or to speculate on future changes in interest rates.
A call swaption or receiver swaption allows the option buyer to enter into an interest-rate swap in which the buyer of the call swaption option pays the floating-rate payments and receives the fixed-rate payments.
The call swaption is exercised if the holder decides to enter into a swap agreement. The swap typically involves the exchange of fixed-rate payments and floating-rate payments based on a specified notional amount. A call swaption has an expiration date, which represents the last date on which the holder can exercise the option. After the expiration date, the option becomes void. The strike rate, also known as the exercise rate, is the fixed rate at which the holder will receive payments in the underlying swap if they choose to exercise the call swaption. The holder of a call swaption typically pays a premium to the counterparty or seller of the swaption in exchange for the right to exercise the option.
A put swaption or payer swaption allows the option buyer to enter into an interest-rate swap in which the buyer of the put swaption pays the fixed-rate payments and received the floating-rate payments.
The put swaption is exercised if the holder decides to enter into a swap agreement. The swap typically involves the exchange of fixed-rate payments and floating-rate payments based on a specified notional amount. A put swaption has an expiration date, which represents the last date on which the holder can exercise the option. After the expiration date, the option becomes void. The strike rate, also known as the exercise rate, is the fixed rate at which the holder will pay payments in the underlying swap if they choose to exercise the put swaption. The holder of a put swaption typically pays a premium to the counterparty or seller of the swaption in exchange for the right to exercise the option.
Version History
Introduced in R2020aYou can price Swaption instruments using a CoxIngersollRoss model object
and an IRTree pricing
method.
Although Swaption supports serial date numbers,
datetime values are recommended instead. The
datetime data type provides flexible date and time
formats, storage out to nanosecond precision, and properties to account for time
zones and daylight saving time.
To convert serial date numbers or text to datetime values, use the datetime function. For example:
t = datetime(738427.656845093,"ConvertFrom","datenum"); y = year(t)
y =
2021
There are no plans to remove support for serial date number inputs.
See Also
Functions
Swap|finmodel|finpricer|volatilities
Topics
- Calibrate Shifted SABR Model Parameters for Swaption Instrument
- Price a Swaption Using SABR Model and Analytic Pricer
- Get Started with Workflows Using Object-Based Framework for Pricing Financial Instruments
- Choose Instruments, Models, and Pricers
- Supported Exercise Styles
- Work with Negative Interest Rates Using Objects
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.
选择网站
选择网站以获取翻译的可用内容,以及查看当地活动和优惠。根据您的位置,我们建议您选择:。
您也可以从以下列表中选择网站:
如何获得最佳网站性能
选择中国网站(中文或英文)以获得最佳网站性能。其他 MathWorks 国家/地区网站并未针对您所在位置的访问进行优化。
美洲
- América Latina (Español)
- Canada (English)
- United States (English)
欧洲
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)