Ways to Construct fi Objects

You can create a fi object by using a fi constructor function or you can build fi object constructors using the Insert fi Constructor dialog box. You can also use a fi constructor function to copy an existing fi object.

numerictype and fimath properties can be specified directly in the fi constructor function or you can use an existing numerictype or fimath object to construct a fi object. The value of a property is taken from the last time it is set.

You can write a reusable MATLAB^® algorithm by keeping the data types of the algorithmic variables in a separate types table.

Use `fi` Constructor to Create `fi` Objects

These examples show you several different ways to construct fi objects.

Construct `fi` Object with Default Data Type and Property Values

Create a fi object with the default data type and a value of 0.

a = fi(0)

a =
 
     0


          DataTypeMode: Fixed-point: binary point scaling
            Signedness: Signed
            WordLength: 16
        FractionLength: 15

The default fi constructor syntax creates a signed fi object with a value of 0, word length of 16 bits, and fraction length of 15 bits.

Note

The fi constructor creates the fi object using a RoundingMethod of Nearest and an OverflowAction of Saturate. If you construct a fi from floating-point values, the default RoundingMethod and OverflowAction property settings are not used.

For information on the display format of fi objects, refer to View Fixed-Point Data.

Copy a `fi` Object

To copy a fi object, use assignment.

a = fi(pi)

a =
 
    3.1416

          DataTypeMode: Fixed-point: binary point scaling
            Signedness: Signed
            WordLength: 16
        FractionLength: 13

b = a

b =
 
    3.1416

          DataTypeMode: Fixed-point: binary point scaling
            Signedness: Signed
            WordLength: 16
        FractionLength: 13

Construct `fi` Object with Property Name-Value Pair Arguments

You can use property name-value pair arguments to set fi object properties in the fi constructor. The fi object has three types of properties:

For example, specify the fimath object properties for the rounding method and overflow action to use when performing fixed-point arithmetic.

a = fi(pi,'RoundingMethod','Floor',...
    'OverflowAction','Wrap')

a = 

    3.1415

          DataTypeMode: Fixed-point: binary point scaling
            Signedness: Signed
            WordLength: 16
        FractionLength: 13

        RoundingMethod: Floor
        OverflowAction: Wrap
           ProductMode: FullPrecision
               SumMode: FullPrecision

If you specify at least one fimath object property in the fi constructor, the fi object has a local fimath object. The fi object uses default values for the remaining unspecified fimath object properties.

If you do not specify any fimath object properties in the fi object constructor, the fi object uses default fimath values and has no local fimath.

You can use the isfimathlocal function to determine whether a fi object has a local fimath associated with it.

Construct `fi` Object Using `numerictype` Object

You can create a fi object using a numerictype object. The numerictype Properties define the data type and scaling attributes of a fi object.

Create a numerictype object with default property values.

T = numerictype

T =
 

          DataTypeMode: Fixed-point: binary point scaling
            Signedness: Signed
            WordLength: 16
        FractionLength: 15

Create a fi object from the numerictype object T.

a = fi(pi,T)

 a =
 
    1.0000


          DataTypeMode: Fixed-point: binary point scaling
            Signedness: Signed
            WordLength: 16
        FractionLength: 15

You can use a fimath object and a numerictype object in the fi constructor.

F = fimath('RoundingMethod','Nearest',...
    'OverflowAction','Saturate',...
    'ProductMode','FullPrecision',...
    'SumMode','FullPrecision')

F =
 
        RoundingMethod: Nearest
        OverflowAction: Saturate
           ProductMode: FullPrecision
               SumMode: FullPrecision

a = fi(pi,T,F)

a =
 
    1.0000


          DataTypeMode: Fixed-point: binary point scaling
            Signedness: Signed
            WordLength: 16
        FractionLength: 15

        RoundingMethod: Nearest
        OverflowAction: Saturate
           ProductMode: FullPrecision
               SumMode: FullPrecision

Note

The syntax a = fi(pi,T,F) is equivalent to a = fi(pi,F,T). You can use both statements to define a fi object using a fimath object and a numerictype object.

Construct `fi` Object Using `fimath` Object

You can create a fi object using a specific fimath object. When you do so, a local fimath object is assigned to the fi object you create. If you do not specify any numerictype object properties, the word length of the fi object defaults to 16 bits. The fraction length is determined by best precision scaling.

For example, create a fimath object that specifies the rounding method, overflow action, product mode, and sum mode to use.

F = fimath('RoundingMethod','Nearest',...
    'OverflowAction','Saturate',...
    'ProductMode','FullPrecision',...
    'SumMode','FullPrecision')

F =
 

             RoundingMethod: Nearest
          OverflowAction: Saturate
           ProductMode: FullPrecision
               SumMode: FullPrecision

Use dot notation to change the overflow action of the fimath object F.

F.OverflowAction = 'Wrap'

F =
 

             RoundingMethod: Nearest
          OverflowAction: Wrap
           ProductMode: FullPrecision
               SumMode: FullPrecision

Create a fi object using the fimath object F.

 a = fi(pi,F)

a =
 
    3.1416

          DataTypeMode: Fixed-point: binary point scaling
            Signedness: Signed
            WordLength: 16
        FractionLength: 13

        RoundingMethod: Nearest
        OverflowAction: Wrap
           ProductMode: FullPrecision
               SumMode: FullPrecision

You can also create fi objects using a fimath object while specifying various numerictype properties at creation time. For example, create an unsigned fi object with a value of pi, word length of 8 bits, fraction length of 6 bits, and fimath F.

b = fi(pi,0,8,6,F)

b = 

    3.1406

          DataTypeMode: Fixed-point: binary point scaling
            Signedness: Unsigned
            WordLength: 8
        FractionLength: 6

        RoundingMethod: Nearest
        OverflowAction: Wrap
           ProductMode: FullPrecision
               SumMode: FullPrecision

Use the Insert fi Constructor Dialog Box to Build `fi` Object Constructors

You can build fi object constructors in MATLAB by using the Insert fi Constructor dialog box. After specifying the value and properties of the fi object in the dialog box, you can insert the prepopulated fi object constructor at a specific location in your file.

For example, create a signed fi object with a value of pi, a word length of 16 bits and a fraction length of 13 bits.

On the MATLAB Home tab, in the File section, click New Script.
On the Editor tab, in the Code section, click the Specify fixed-point data button arrow . Click Insert fi to open the Insert fi Constructor dialog box.
Use the edit boxes and drop-down menus to specify the following properties of the fi object:
- Value = pi
- Data type mode = Fixed-point: binary point scaling
- Signedness = Signed
- Word length = 16
- Fraction length = 13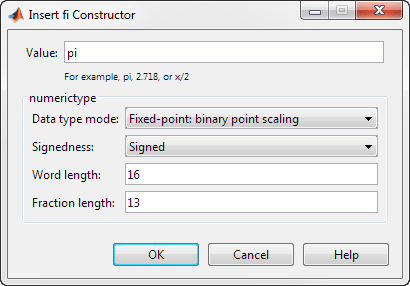
To insert the fi object constructor in your file, place your cursor at the desired location in the file, then click OK on the Insert fi Constructor dialog box. Clicking OK closes the Insert fi Constructor dialog box and automatically populates the fi object constructor in your file.
```
fi(pi, 1, 16, 13)
```

Determine Property Precedence

The value of a property of a fi object is taken from the last time it is set. For example, create a numerictype object with the Signed set to true and a fraction length of 14.

T = numerictype('Signed',true,...
    'FractionLength',14)

T =
 

          DataTypeMode: Fixed-point: binary point scaling
            Signedness: Signed
            WordLength: 16
        FractionLength: 14

Create a fi object that specifies the numerictype property T after the Signed property. The resulting fi object is signed.

a = fi(pi,'Signed',false,...
    'numerictype',T)

a =
 
    1.9999

          DataTypeMode: Fixed-point: binary point scaling
            Signedness: Signed
            WordLength: 16
        FractionLength: 14

Create a second fi object that specifies the numerictype T before the Signed property. The resulting fi object is unsigned.

b = fi(pi,'numerictype',T,...
    'Signed',false)

b =
 
    3.1416

          DataTypeMode: Fixed-point: binary point scaling
            Signedness: Unsigned
            WordLength: 16
        FractionLength: 14

Create `fi` Objects for Use in a Types Table

You can write a reusable MATLAB algorithm by keeping the data types of the algorithmic variables in a separate types table. For example,

function T = mytypes(dt)
  switch dt
    case 'double'
      T.b = double([]);
      T.x = double([]);
      T.y = double([]);

     case 'fixed16'
      T.b = fi([],1,16,15);
      T.x = fi([],1,16,15);
      T.y = fi([],1,16,14);
  end
end

Cast the variables in the algorithm to the data types in the types table as described in Manual Fixed-Point Conversion Best Practices.

function [y,z]=myfilter(b,x,z,T)
  y = zeros(size(x),'like',T.y);
  for n=1:length(x)
    z(:) = [x(n); z(1:end-1)];
    y(n) = b * z;
  end
end

In a separate test file, set up input data to feed into your algorithm, and specify the data types of the inputs.

% Test inputs
b = fir1(11,0.25);
t = linspace(0,10*pi,256)';
x = sin((pi/16)*t.^2); 
% Linear chirp

% Cast inputs
T=mytypes('fixed16');
b=cast(b,'like',T.b);
x=cast(x,'like',T.x);
z=zeros(size(b'),'like',T.x);

% Run
[y,z] = myfilter(b,x,z,T);