Implement Hardware-Efficient Complex Divide HDL Optimized

Division of Complex Numbers

The division operation for two complex numbers $$a+bi$$ and $$c+di$$, where $\mathit{b}\ne 0$, is defined as $$z=\frac{a+bi}{c+di}$$. After multiplying the denominator by its complex conjugate, this can be re-written as $$z=\frac{(ac+bd)+(bc-ad)i}{c^2+d^2}$$.

The CORDIC Algorithm

CORDIC is an acronym for COordinate Rotation DIgital Computer, and can be used to efficiently compute many trigonometric, hyperbolic, and arithmetic functions.

Fully Pipelined Fixed-Point Computations

The Complex Divide HDL Optimized block supports HDL code generation for fixed-point data with binary-point scaling. It is designed with this application in mind, and employs hardware specific semantics and optimizations. One of these optimizations is pipelining its entire internal circuitry to maintain a very high throughput.

When deploying intricate algorithms to FPGA or ASIC devices, there is often a tradeoff between resource usage and total throughput for a given computation. Resource-sharing often reduces the resources consumed by a design, but also reduces the throughput in the process. Simple arithmetic and trigonometic computations, which typically form parts of bigger computations, require high throughput to drive circuits further in the design. Thus, fully pipelined implementations consume more on-chip resources but are beneficial in large designs.

All of the key computational units in the Complex Divide HDL Optimized block are fully pipelined internally. This includes not only the CORDIC circuitry used to perform the Givens rotations, but also the adders and shifters used elsewhere in the design, thus ensuring maximum throughput.

Interfacing with the Complex Divide HDL Optimized Block

Because of its fully pipelined nature, the Complex Divide HDL Optimized block is able to accept input data on any cycle, including consecutive cycles. To send input data to the block, the validIn signal must be set to true. When the block has finished the computation and is ready to send the output, it will set validOut to true for one clock cycle. For inputs sent on consecutive cycles, validOut will also be set to true on consecutive cycles. Both the numerator and the denominator must be sent together on the same cycle.

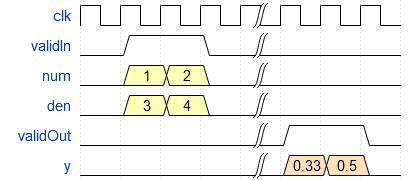
Open the Model and Define Input Data

To open the example model, at the command line, enter:

mdl = 'fxpdemo_complexDivide';
open_system(mdl)

The model contains the Complex Divide HDL Optimized block connected to a data source which takes in arrays of inputs (numerators and denominators) and passes an input value from each array to the block on consecutive cycles. The output computed for each value is stored in a workspace variable. The simulation terminates when all inputs have been processed.

Define arrays of inputs complexDivideNumerators and complexDivideDenominators. For this example, the inputs are doubles. Note that both the numerator and the denominator should have the same datatype.

rng('default');
complexDivideNumerators = (9*rand(1000,1) + 1) + (9*rand(1000,1) + 1)*1i;
complexDivideDenominators = (9*rand(1000,1) + 1) + (9*rand(1000,1) + 1)*1i;

Define the output dataype to be used in the model. For this example, the outputs are also doubles. Note that fixed-point type outputs can only be used with fixed-point type inputs.

OutputType = 'double';

Simulate the Model and Examine the Output

Simulate the model.

sim(mdl);

When the simulation is complete, a new workspace variable, complexDivideOutputs, is created to hold the computed value for each pair of inputs.

Examine the error of the calculation by comparing the output of the Complex Divide HDL Optimized block to that of the built-in MATLAB divide function.

expectedOutput = complexDivideNumerators./complexDivideDenominators;
actualOutput = complexDivideOutputs;
maxError = max(abs(expectedOutput - actualOutput))

maxError = 
5.6173e-15