How to Efficiently Track Large Numbers of Objects

Introduction

In many applications, trackers are required to track hundreds or thousands of objects. Increasing the number of tracks maintained by a tracker is a challenge, caused by the computational complexity of the algorithm at the core of every tracker. In particular, two common stages in the tracker update step are not easily scalable: calculating the assignment cost and performing the assignment. Assignment cost calculation is common to trackerGNN, trackerJPDA, and trackerTOMHT, and the techniques shown in this example can be applied when using any of these trackers. The way each tracker performs the assignment is unique to each tracker, and may require tailored solutions to improve the tracker performance, which are beyond the scope of this example.

Scenario

For the purposes of this example, you define a scenario that contains 900 platforms, organized in a 15-by-15 grid, with each grid cell containing 4 platforms. The purpose of the grid cells is to demonstrate the benefit of coarse cost calculation, explained later in the example.

The following code arranges the 900 objects in the grid cell and creates the visualization. On the left, the entire scenario is shown. On the right, the visualization zooms in on 4 grid cells. Note each cell contains 4 platforms.

[platforms,tp,zoomedtp] = createPlatforms;

Use the Default Assignment Cost Calculation

This section shows the results of tracking the platforms defined above using a trackerGNN with default AssignmentThreshold. The AssignmentThreshold property contains two values: [C1 C2], where C1 is the threshold used for the assignment and C2 is a threshold for coarse calculation explained in the next section.

When the tracker is updated with a new set of detections, it calculates the cost of assigning every detection to every track. The accurate cost calculation must take into account the measurement and uncertainty of each detection as well as the expected measurement and expected uncertainty from each track, as depicted below.

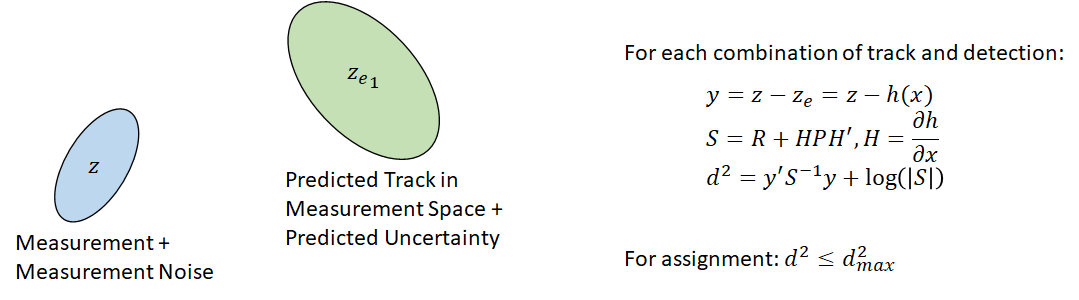
By default, C2 is set to Inf, which requires that the costs of all combinations of track and detection are calculated. This leads to a more accurate assignment, but is more computationally intensive. You should start with the default setting to make sure the tracker assigns detections to tracks in the best way, and then consider lowering the value of C2 to reduce the time required for calculating the assignment cost.

During assignment cost calculation, elements of the cost matrix whose values are higher than C1 are replaced with Inf. Doing so helps the assignment algorithm to ignore impossible assignments.

Define a tracker that can track up to 1000 tracks. The tracker uses the default constant velocity extended Kalman filter, and its state is defined as [x;vx;y;vy;z;vz], which is used by the positionSelector below to get the position components.

tracker = trackerGNN('MaxNumTracks',1000, 'AssignmentThreshold', [30 Inf]);
positionSelector = [1 0 0 0 0 0; 0 0 1 0 0 0; 0 0 0 0 0 0];

On the first call to step, the tracker instantiates all tracks. To isolate the time required to instantiate the tracks from the processing time required for the first step, you can call setup and reset before stepping the tracker. See the supporting function runTracker at the end of this example for more details.

[trkSummary,truSummary,info] = runTracker(platforms,tracker,positionSelector,tp,zoomedtp);

Tracker set up time: 8.3108
Step 1 time: 3.7554
Step 2 time: 15.3029
Step 3 time: 14.1099
Step 4 time: 14.3506
Step 5 time: 14.3963

All steps from now are without detections.
Step 6 time: 0.53103
Step 7 time: 0.52582
Step 8 time: 0.50639
Step 9 time: 0.50909
Step 10 time: 0.16034
Scenario done. All tracks are now deleted.

You analyze the tracking results by examining the track assignment metrics values. For perfect tracking the total number of tracks should be equal to the number of platforms and there should be no false, swapped, or divergent tracks. Similarly, there should be no missing truth or breaks in the truth summary.

assignmentMetricsSummary(trkSummary,truSummary)

Track assignment metrics summary:
    TotalNumTracks    NumFalseTracks    MaxSwapCount    MaxDivergenceCount    MaxDivergenceLength
    ______________    ______________    ____________    __________________    ___________________

         900                0                0                  0                      0         

Truth assignment metrics summary:
    TotalNumTruths    NumMissingTruths    MaxEstablishmentLength    MaxBreakCount
    ______________    ________________    ______________________    _____________

         900                 0                      1                     0      

Use Coarse Assignment Cost Calculation

In the previous section, you saw that the tracker is able to track all the platforms, but every update step takes a long time. Most of the time was spent on calculating the assignment cost matrix.

Examining the cost matrix, you can see that vast majority of its elements are, in fact, Inf.

cm = info.CostMatrix;
disp("Cost matrix has " + numel(cm) + " elements.");
disp("But the number of finite values is " + numel(cm(isfinite(cm))) + newline)

Cost matrix has 810000 elements.
But the number of finite values is 2700

The above result shows that the cost calculation spends too much time on calculating the assignment cost of all the combinations of track and detection. However, most of these combinations are too far to be assigned, as the actual measurement is too far from the track expected measurement based on the sensor characteristics. To avoid the waste in calculating all the costs, you can use coarse cost calculation.

Coarse calculation is done to verify which combinations of track and detection may require an accurate normalized distance calculation. Only combinations whose coarse assignment cost is lower than C2 are calculated accurately. The coarse cost calculation is depicted in the image below. A detection is represented by its measurement and measurement noise . Two tracks are predicted to the time of the detection and projected to the measurement space, depicted by the points and . Note that the track uncertainty is not projected to the measurement space, which allows us to vectorize the coarse calculation. This is a rough estimate, because only the uncertainty around the detection is taken into account. In the depicted example, the first track falls outside of the coarse calculation gate while the second track falls inside it. Thus, accurate cost calculation is only done for the combination of this detection and the second track.

To use coarse cost calculation, release the tracker and modify its AssignmentThreshold to a value of [30 200]. Then, rerun the tracker.

release(tracker)
tracker.AssignmentThreshold = [30 200];
[trkSummary,truSummary] = runTracker(platforms,tracker,positionSelector,tp,zoomedtp);

Tracker set up time: 6.5846
Step 1 time: 3.5863
Step 2 time: 3.4095
Step 3 time: 2.9347
Step 4 time: 2.8555
Step 5 time: 2.9397

All steps from now are without detections.
Step 6 time: 0.51446
Step 7 time: 0.52277
Step 8 time: 0.54865
Step 9 time: 0.50941
Step 10 time: 0.19085
Scenario done. All tracks are now deleted.

You observe that the steps 3-5 now require significantly less time to complete. Step 2 is also faster than it used to be, but still slower than steps 3-5.

To understand why step 2 is slower, consider the track states after the first tracker update. The states contain position information, but the velocity is still zero. When the tracker calculates the assignment cost, it predicts the track states to the detection times, but since the tracks have zero velocity, they remain in the same position. This results in large distances between the detection measurements and the expected measurements from the predicted track states. These relatively large assignment costs make it harder for the assignment algorithm to find the best assignment, which causes step 2 to take more time than steps 3-5.

It's important to verify that the track assignment with coarse cost calculation remains the same as without it. If the track assignment metrics are not the same, you must increase the size of the coarse calculation gate. The following shows that the tracking is still perfect as it was in the previous section, but each processing step took less time.

assignmentMetricsSummary(trkSummary,truSummary)

Track assignment metrics summary:
    TotalNumTracks    NumFalseTracks    MaxSwapCount    MaxDivergenceCount    MaxDivergenceLength
    ______________    ______________    ____________    __________________    ___________________

         900                0                0                  0                      0         

Truth assignment metrics summary:
    TotalNumTruths    NumMissingTruths    MaxEstablishmentLength    MaxBreakCount
    ______________    ________________    ______________________    _____________

         900                 0                      1                     0      

Use an External Cost Calculation

Another way to control the time it takes to calculate the cost assignment is by using your own assignment cost calculation instead of the default the tracker uses.

An external cost calculation can take into account attributes that are not part of the track state and expected measurement. It can also use different distance metrics, for example Euclidean norm instead of normalized distance. The choice of which cost calculation to apply depends on the specifics of the problem, the measurement space, and how you define the state and measurement.

To use an external cost calculation, you release the tracker and set its HasCostMatrixInput property to true. You must pass your own cost matrix as an additional input with each update to the tracker. See the supporting function runTracker for more details.

release(tracker);
tracker.HasCostMatrixInput = true;
[trkSummary,truSummary] = runTracker(platforms,tracker,positionSelector,tp,zoomedtp);
assignmentMetricsSummary(trkSummary,truSummary)

Tracker set up time: 6.559
Step 1 time: 3.4394
Step 2 time: 1.7852
Step 3 time: 1.474
Step 4 time: 1.5312
Step 5 time: 1.5152

All steps from now are without detections.
Step 6 time: 0.60809
Step 7 time: 0.61374
Step 8 time: 0.616
Step 9 time: 0.63798
Step 10 time: 0.22762
Scenario done. All tracks are now deleted.

Track assignment metrics summary:
    TotalNumTracks    NumFalseTracks    MaxSwapCount    MaxDivergenceCount    MaxDivergenceLength
    ______________    ______________    ____________    __________________    ___________________

         900                0                0                  0                      0         

Truth assignment metrics summary:
    TotalNumTruths    NumMissingTruths    MaxEstablishmentLength    MaxBreakCount
    ______________    ________________    ______________________    _____________

         900                 0                      1                     0      

As expected, the processing time is even lower when using an external cost calculation function.

Change the GNN Assignment Algorithm

Another option to try is using a different GNN assignment algorithm that may be more efficient in finding the assignment by modifying the Assignment property of the tracker.

release(tracker)
tracker.Assignment = 'Jonker-Volgenant';
tracker.HasCostMatrixInput = true;
runTracker(platforms,tracker,positionSelector,tp,zoomedtp);

Tracker set up time: 6.494
Step 1 time: 3.5346
Step 2 time: 1.894
Step 3 time: 3.1192
Step 4 time: 3.1212
Step 5 time: 3.1458

All steps from now are without detections.
Step 6 time: 0.61109
Step 7 time: 0.62456
Step 8 time: 0.61849
Step 9 time: 0.60604
Step 10 time: 0.22303
Scenario done. All tracks are now deleted.

The Jonker-Volgenant algorithm performs the assignment in the second step faster relative to the default Munkres algorithm.

Monte-Carlo Simulation

If you want to run multiple scenarios without modifying the tracker settings, there is no need to call the release method. Instead, just call the reset method to clear previous track information from the tracker. This way, you save the time required to instantiate all the tracks. Note the "Tracker set up time" below relative to previous runs.

reset(tracker)
runTracker(platforms,tracker,positionSelector,tp,zoomedtp);

Tracker set up time: 0.097531
Step 1 time: 3.4684
Step 2 time: 1.6592
Step 3 time: 3.1429
Step 4 time: 3.1274
Step 5 time: 3.0994

All steps from now are without detections.
Step 6 time: 0.63232
Step 7 time: 0.61857
Step 8 time: 0.61433
Step 9 time: 0.60698
Step 10 time: 0.25301
Scenario done. All tracks are now deleted.

Summary

This example showed how to track large numbers of objects. When tracking many objects, the tracker spends a large fraction of the processing time on computing the cost assignment for each combination of track and detection. You saw how to use the cost calculation threshold to improve the time spent on calculating the assignment cost. In addition, the example showed how to use an external cost calculation, which may be designed to be more computationally efficient for the particular tracking problem you have.

You can reduce the cost assignment threshold or use an external cost calculation to improve the speed of the trackerJPDA and the trackerTOMHT as well.

Supporting Functions

createPlatforms

This function creates the platforms in a 20x20 grid with 2x2 platforms per grid cell.

function [platforms,tp,zoomedtp] = createPlatforms
% This is a helper function to run the tracker and display the results. It
% may be removed in the future.
nh  = 15; % Number of horizontal grid cells
nv  = 15; % Number of vertical grid cells
nsq = 2;  % 2x2 platforms in a grid cell
nPl = nh*nv*nsq^2; % Overall number of platforms
xgv = sort(-50 + repmat(100 * (1:nh), [1 nsq]));
ygv = sort(-50 + repmat(100 * (1:nv), [1 nsq]));
[X,Y] = meshgrid(xgv,ygv);

npts = nsq/2;
xshift = 10*((-npts+1):npts) -5;
yshift = xshift;

xadd = repmat(xshift, [1 nh]);
yadd = repmat(yshift, [1 nv]);

[Xx, Yy] = meshgrid(xadd,yadd);

X = X + Xx;
Y = Y + Yy;
pos = [X(:),Y(:),zeros(numel(X),1)];

% The following creates an array of struct for the platforms, which are
% used later for track assignment metrics.
vel = [3 1 0]; % Platform velocity
platforms = repmat(struct('PlatformID', 1, 'Position', [0 0 0], 'Velocity', vel),nPl,1);
for i = 1:nPl
    platforms(i).PlatformID  = i;
    platforms(i).Position(:) = pos(i,:);
end

% Visualization
f = figure('Position',[1 1 1425 700]);
movegui center;
h1 = uipanel(f,'FontSize',12,'Position',[.01 .01 .48 .98],"Title","Scene View");
a1 = axes(h1,'Position',[0.05 0.05 0.9 0.9]);
tp = theaterPlot('Parent', a1, 'XLimits',[0 nh*100], 'YLimits',[0 nv*100]);
set(a1,'XTick',0:100:nh*100)
set(a1,'YTick',0:100:nv*100)
grid on
pp = trackPlotter(tp,'Tag','Truth','Marker','^','MarkerEdgeColor','k','MarkerSize',4,'HistoryDepth',10);
plotTrack(pp,reshape([platforms.Position],3,[])');
trackPlotter(tp, 'Tag','Tracks','MarkerEdgeColor','b','MarkerSize',6,'HistoryDepth',10);
c = get(a1.Parent,'Children');
for i = 1:numel(c)
    if isa(c(i),'matlab.graphics.illustration.Legend')
        set(c(i),'Visible','off')
    end
end

h2 = uipanel(f,'FontSize',12,'Position',[.51 .01 .48 .98],'Title','Zoomed View');
a2 = axes(h2,'Position',[0.05 0.05 0.9 0.9]);
zoomedtp = theaterPlot('Parent', a2, 'XLimits',[400 500], 'YLimits',[400 500]);
set(a2,'XTick',400:100:500)
set(a2,'YTick',400:100:500)
grid on
zoomedpp = trackPlotter(zoomedtp,'DisplayName','Truth','Marker','^','MarkerEdgeColor','k','MarkerSize',6,'HistoryDepth',10);
plotTrack(zoomedpp,reshape([platforms.Position],3,[])');
trackPlotter(zoomedtp, 'DisplayName','Tracks','MarkerEdgeColor','b','MarkerSize',8,'HistoryDepth',10,'ConnectHistory','on','FontSize',1);
end

runTracker

This function runs the tracker, updates the plotters, and gathers track assignment metrics.

function [trkSummary,truSummary,info] = runTracker(platforms,tracker,positionSelector,tp,zoomedtp)
% This is a helper function to run the tracker and display the results. It
% may be removed in the future.

pp = findPlotter(tp,'Tag','Truth');
trp = findPlotter(tp, 'Tag','Tracks');
zoomedpp = findPlotter(zoomedtp,'DisplayName','Truth');
zoomedtrp = findPlotter(zoomedtp, 'DisplayName','Tracks');

% To save time, pre-allocate all the detections and assign them on the fly.
nPl = numel(platforms);
det = objectDetection(0,[0;0;0]);
dets = repmat({det},[nPl,1]);

% Define a track assignment metrics object.
tam = trackAssignmentMetrics;

% Bring the visualization back.
set(tp.Parent.Parent.Parent,'Visible','on')

hasExternalCostFunction = tracker.HasCostMatrixInput;

% Measure the time it takes to set the tracker up.
tic
if ~isLocked(tracker)
    if hasExternalCostFunction
        setup(tracker,dets,0,0);
    else
        setup(tracker,dets,0);
    end
end
reset(tracker)
disp("Tracker set up time: " + toc);

% Run 5 steps with detections for all the platforms.
for t = 1:5
    for i = 1:nPl
        dets{i}.Time = t;
        dets{i}.Measurement = platforms(i).Position(:);
    end

    tic
    if hasExternalCostFunction
        if isLocked(tracker)
            % Use predictTracksToTime to get all the predicted tracks.
            allTracks = predictTracksToTime(tracker,'all',t);
        else
            allTracks = [];
        end
        costMatrix = predictedEuclidean(allTracks,dets,positionSelector);
        [tracks,~,~,info] = tracker(dets,t,costMatrix);
    else
        [tracks,~,~,info] = tracker(dets,t);
    end
    trPos = getTrackPositions(tracks, positionSelector);
    trIDs = string([tracks.TrackID]');
    disp("Step " + t + " time: " + toc)

    % Update the plot.
    plotTrack(pp,reshape([platforms.Position],3,[])');
    plotTrack(trp,trPos);
    plotTrack(zoomedpp,reshape([platforms.Position],3,[])');
    plotTrack(zoomedtrp,trPos,trIDs);
    drawnow

    % Update the track assignment metrics object.
    if nargout
        [trkSummary, truSummary] = tam(tracks,platforms);
    end

    % Update the platform positions.
    for i = 1:nPl
        platforms(i).Position = platforms(i).Position + platforms(i).Velocity;
    end
end
snapnow

% Run steps with no detections until the tracker deletes all the tracks.
disp("All steps from now are without detections.")
while ~isempty(tracks)
    t = t+1;
    tic
    if hasExternalCostFunction
        allTracks = predictTracksToTime(tracker,'all',t);
        costMatrix = predictedEuclidean(allTracks,{},positionSelector);
        tracks = tracker({},t,costMatrix);
    else
        tracks = tracker({},t);
    end
    disp("Step " + t + " time: " + toc)

    % Update the position of the tracks to plot.
    trPos = getTrackPositions(tracks,positionSelector);
    trIDs = string([tracks.TrackID]');

    % Update the plot.
    plotTrack(pp,reshape([platforms.Position],3,[])');
    plotTrack(trp,trPos);
    plotTrack(zoomedpp,reshape([platforms.Position],3,[])');
    plotTrack(zoomedtrp,trPos,trIDs);
    drawnow

    % Update the platform positions.
    for i = 1:nPl
        platforms(i).Position = platforms(i).Position + platforms(i).Velocity;
    end
end
disp("Scenario done. All tracks are now deleted." + newline)
clearData(pp)
clearData(trp)
clearData(zoomedpp)
clearData(zoomedtrp)
set(tp.Parent.Parent.Parent,'Visible','off') % Prevent excessive snapshots
drawnow
end

predictedEuclidean

The function calculates the Euclidean distance between measured positions from detections and predicted positions from tracks.

function euclidDist = predictedEuclidean(tracks,detections,positionSelector)
% This is a helper function to run the tracker and display the results. It
% may be removed in the future.

if isempty(tracks) || isempty(detections)
    euclidDist = zeros(numel(tracks),numel(detections));
    return
end

predictedStates = [tracks.State];
predictedPositions = positionSelector * predictedStates;
dets = [detections{:}];
measuredPositions = [dets.Measurement];
euclidDist = zeros(numel(tracks),numel(detections));
for i = 1:numel(detections)
    diffs = bsxfun(@minus, predictedPositions',measuredPositions(:,i)');
    euclidDist(:,i) = sqrt(sum((diffs .* diffs),2));
end
end

assignmentMetricsSummary

The function displays the key assignment metrics in a table form.

function assignmentMetricsSummary(trkSummary,truSummary)
trkSummary = rmfield(trkSummary, {'TotalSwapCount','TotalDivergenceCount',...
    'TotalDivergenceLength','MaxRedundancyCount','TotalRedundancyCount',...
    'MaxRedundancyLength','TotalRedundancyLength'});
truSummary = rmfield(truSummary, {'TotalEstablishmentLength','TotalBreakCount',...
    'MaxBreakLength','TotalBreakLength'});
trkTable = struct2table(trkSummary);
truTable = struct2table(truSummary);
disp("Track assignment metrics summary:")
disp(trkTable)
disp("Truth assignment metrics summary:")
disp(truTable)
end