Fuzzy Logic Control for House Heating System

Since R2024b

This example uses:

This example shows how to control the thermal dynamics of a house using fuzzy inference systems. The fuzzy controller uses two fuzzy systems:

The first fuzzy inference system (FIS) calculates a desired room temperature based on the current outdoor temperature, the current electricity price, and a user-specified comfort-level.
The second fuzzy system uses a fuzzy PID controller to regulate the heater power for maintaining the desired room temperature.

House Heating System

The house heating system, implemented using Simscape™ blocks, contains a heater and a house structure.

model = "houseHeatingSystemWithFuzzyControl";
open_system(model)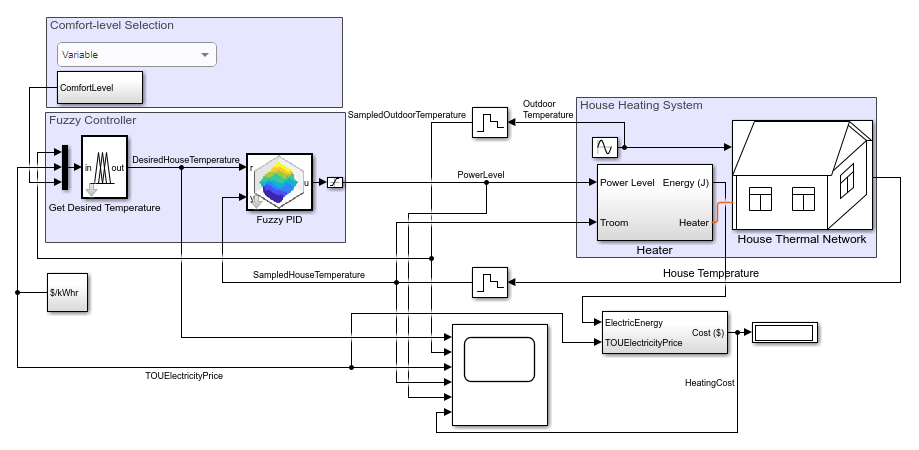

The house structure includes four parts: inside air, house walls, windows, and roof. The house exchanges heat with the environment through its walls, windows, and roof. Each path is simulated as a combination of thermal convection, thermal conduction, and thermal mass.

open_system(model+"/House Thermal Network")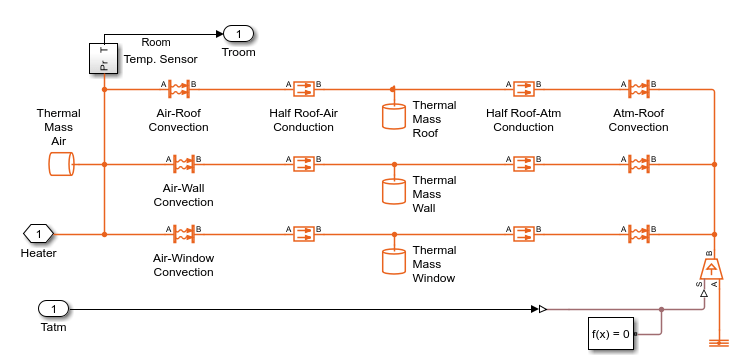

The heater uses electrical energy for heating the house with a specified power level in the range [0, 1], where 0 and 1 indicate the minimum and maximum power levels, respectively.

open_system(model+"/Heater")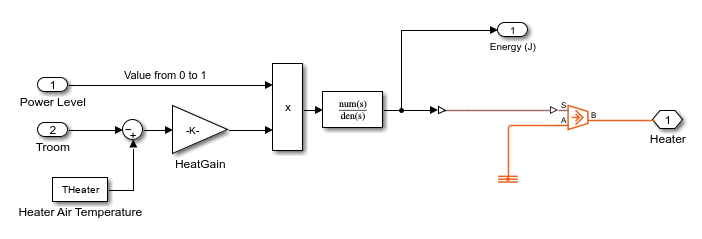

The heating system uses a temperature sensor to get room temperature feedback in every 300 seconds (5 minutes). It uses another sensor to get outdoor ambient temperature feedback, with the same sample time synced with the room temperature sensor, for temperature control.

Control Objectives

A fuzzy inference system (FIS) based controller regulates the power level of the heater to achieve the following objectives:

Maintain the house (or room) temperature within a comfortable zone of [20 $°$ C, 22 $°$ C], while the outdoor temperature can vary between [4 $°$ C, 12 $°$ C].
Provide three comfort-level settings: minimum, variable, and maximum.

The minimum comfort level regulates the power level to maintain 20 $°$ C room temperature for cost minimization, whereas the maximum comfort level regulates the power to maintain 22 $°$ C room temperature, which produces a higher heating cost. The variable comfort level regulates the heater power to increase the room temperature (within the comfortable zone) while keeping the heating cost low (in between the minimum and maximum levels).

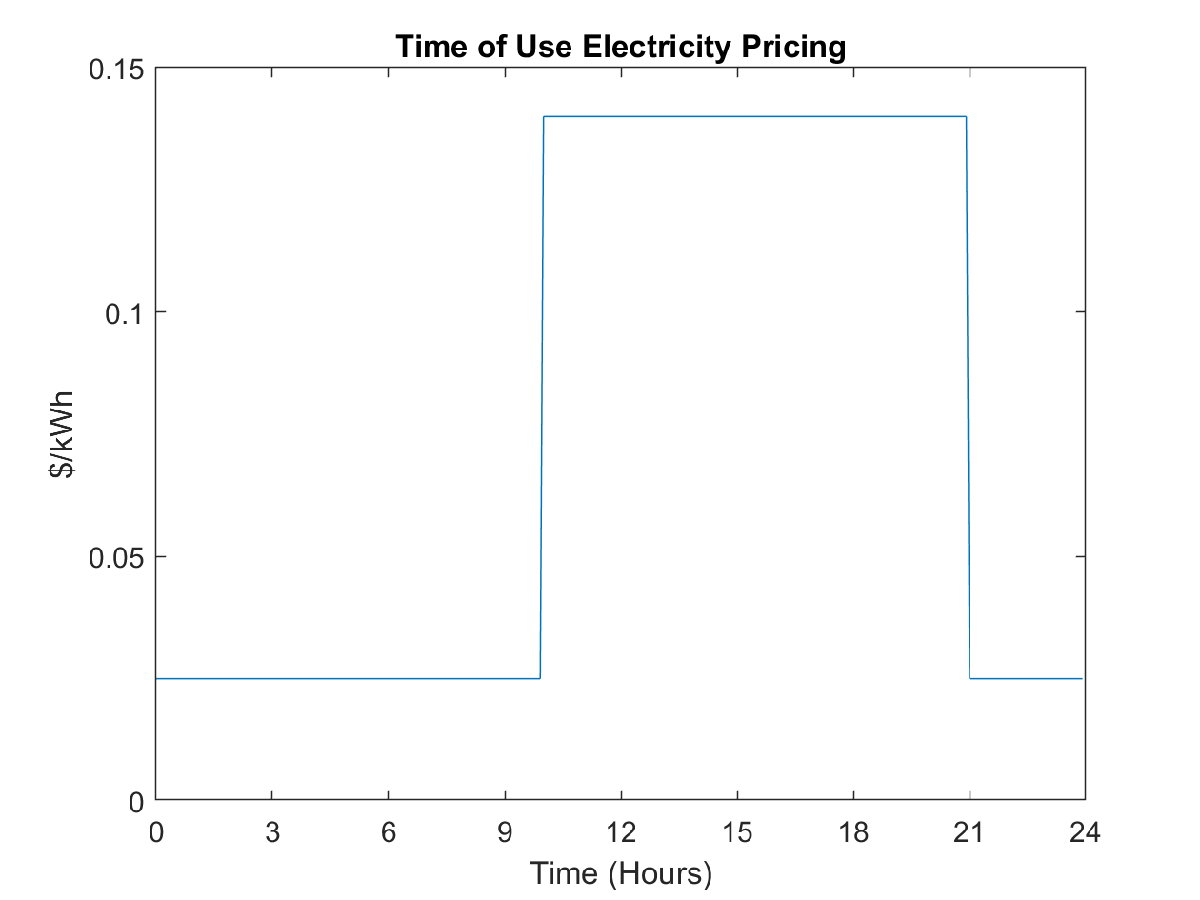
In this example, electricity price fluctuates during the day. As shown in the following figure, the heating cost is most expensive between 10 a.m. and 9 p.m. Therefore, in the variable comfort-level, the fuzzy logic controller increases the room temperature when the electricity price is low and the outdoor temperature is high.

time of use electricity pricing.png

Fuzzy Logic Controller

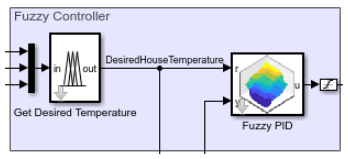
The following Simulink (model) diagram shows a FIS-based fuzzy controller for the house heating system.

The fuzzy controller for this example uses two fuzzy systems:

The Get Desired Temperature system is a Fuzzy Logic Controller block that calculates the desired room temperature.
The Fuzzy PID system is a Fuzzy PID Controller block that regulates the heater power for maintaining the desired room temperature.

FIS for Calculating Desired Room Temperature

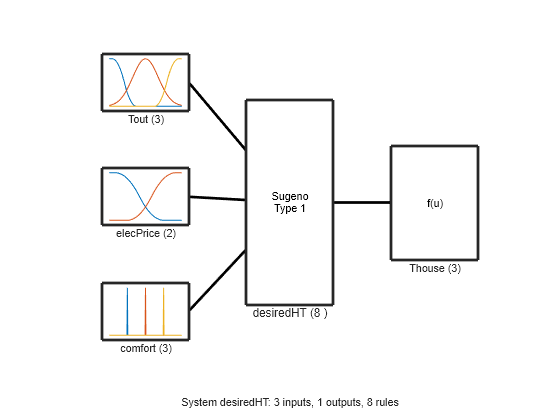
The first fuzzy inference system calculates a desired room temperature based on the current outdoor temperature, the current electricity price, and a user-specified comfort-level.

You can load a presaved FIS using the following command.

desiredHT = readfis('desiredHT.fis');

Alternatively, you can construct the FIS. First, create a Sugeno FIS object.

desiredHT = sugfis(Name="desiredHT");

Define the input variable for the outdoor temperature using three membership functions across the range [4,12].

desiredHT = addInput(desiredHT,[4 12],Name="Tout");
desiredHT = addMF(desiredHT,"Tout","zmf",[4.333 7],Name="low");
desiredHT = addMF(desiredHT,"Tout","gaussmf",[1.416 8],Name="medium");
desiredHT = addMF(desiredHT,"Tout","smf",[9 11.67],Name="high");

Define the input variable for the price of electricity using two membership functions across the range [0,0.15].

desiredHT = addInput(desiredHT,[0 0.15],Name="elecPrice");
desiredHT = addMF(desiredHT,"elecPrice", ...
    "zmf",[0.0125 0.1125],Name="low");
desiredHT = addMF(desiredHT,"elecPrice", ...
    "smf",[0.0375 0.1375],Name="high");

Define the input variable for the user-specified comfort level. This variable represents each comfort level as a crisp singleton membership function implemented using a triangular membership function.

desiredHT = addInput(desiredHT,[0 4],Name="comfort");
desiredHT = addMF(desiredHT,"comfort","" + ...
    "trimf",[1 1 1],Name="minC");
desiredHT = addMF(desiredHT,"comfort", ...
    "trimf",[2 2 2],Name="varC");
desiredHT = addMF(desiredHT,"comfort", ...
    "trimf",[3 3 3],Name="maxC");

Define the output variable for the desired temperature using three membership functions across the range [19,23].

desiredHT = addOutput(desiredHT,[19 23],Name="Thouse");
desiredHT = addMF(desiredHT,"Thouse", ...
    "constant",20,Name="low");
desiredHT = addMF(desiredHT,"Thouse", ...
    "constant",21,Name="medium");
desiredHT = addMF(desiredHT,"Thouse", ...
    "constant",22,Name="high");

Define the fuzzy rule base.

desiredHT = addRule(desiredHT,[ ...
    "Tout==low & elecPrice==low & comfort==varC => Thouse=medium (1)"; ...    
    "Tout==medium & elecPrice==low & comfort==varC => Thouse=medium (1)" ; ...
    "Tout==high & elecPrice==low & comfort==varC => Thouse=high (1)"; ...
    "Tout==low & elecPrice==high & comfort==varC => Thouse=low (1)"; ...
    "Tout==medium & elecPrice==high & comfort==varC => Thouse=medium (1)"; ...
    "Tout==high & elecPrice==high & comfort==varC => Thouse=medium (1)"; ...
    "comfort==minC => Thouse=low (1)"; ...
    "comfort==maxC => Thouse=high (1)" ...
    ]);

Visualize the FIS structure.

figure
plotfis(desiredHT)

For minimum and maximum comfort levels, desiredHT produces 20 $°$ C and 22 $°$ C output values. For the variable comfort-level, desiredHT produces the following output surface.

figure
gensurf(desiredHT)

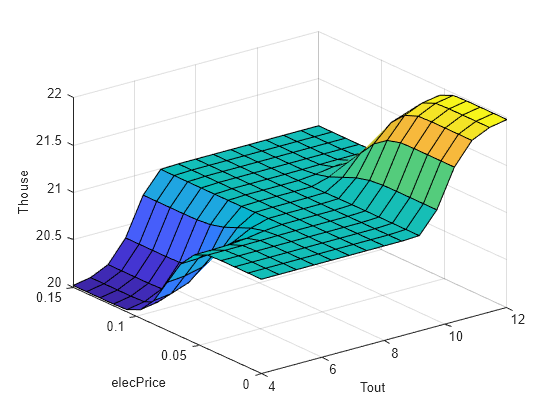
Figure contains an axes object. The axes object with xlabel Tout, ylabel elecPrice contains an object of type surface.

This fuzzy system produces a:

Low temperature setting for a low outdoor temperature and high electricity price. In this case, the energy requirement is relatively high due to higher difference between the outdoor and indoor temperature.
High temperature setting for a high outdoor temperature and low electricity price. In this case, the energy requirement is relatively low due to a lower difference between the outdoor and indoor temperature.
Medium temperature setting for other cases to balance the effects of the electricity price and outdoor temperature.

As a result, the variable comfort-level produces a heating cost between that of the minimum and maximum comfort levels.

Fuzzy PID Controller

In this example, you implement the temperature controller using a Fuzzy PID Controller block.

The fuzzy PID controller block uses the following block settings for this example.

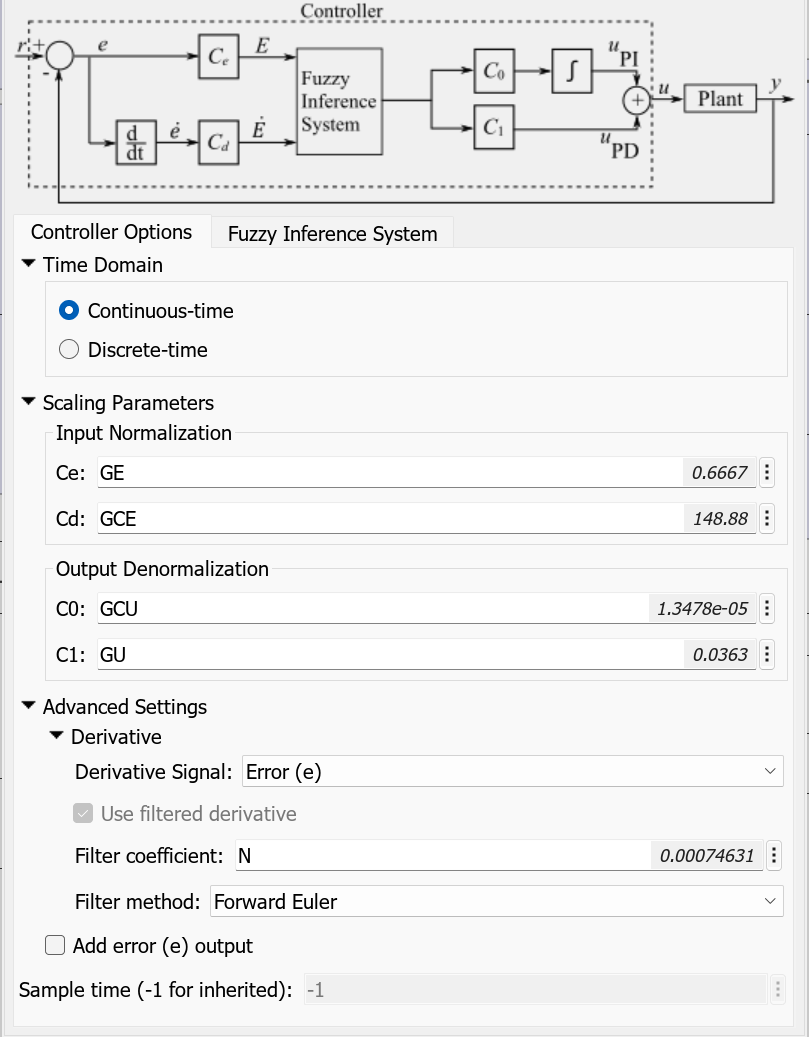
The scaling parameter and the filter coefficient values are tuned to produce better control results.

You can load a presaved controller FIS using the following command.

fpid = readfis('fpid.fis');

Alternatively, you can construct the FIS. First, create a Sugeno FIS object.

fpid = sugfis(Name="fpid");

Define the input variable for the temperature error using two membership functions across the range [-1,1].

fpid = addInput(fpid,[-1 1],Name="error");
fpid = addMF(fpid,"error", ...
    "gaussmf",[0.7 -1],Name="negative");
fpid = addMF(fpid,"error", ...
    "gaussmf",[0.7 1],Name="positive");

Define the input variable for the error rate of change using two membership functions across the range [-1,1].

fpid = addInput(fpid,[-1 1],Name="rate");
fpid = addMF(fpid,"rate", ...
    "gaussmf",[0.7 -1],Name="negative");
fpid = addMF(fpid,"rate", ...
    "gaussmf",[0.7 1],Name="positive");

Define the output variable for the controller action using three membership functions across the range [-2,2].

fpid = addOutput(fpid,[-2 2],Name="u");
fpid = addMF(fpid,"u", ...
    "constant",-2,Name="negative");
fpid = addMF(fpid,"u", ...
    "constant",0,Name="zero");
fpid = addMF(fpid,"u", ...
    "constant",2,Name="positive");

Define the rule base for the controller.

fpid = addRule(fpid,[ ...
    "error==negative & rate==negative => u=negative (1)"; ...
    "error==positive & rate==negative => u=zero (1)"; ...
    "error==negative & rate==positive => u=zero (1)"; ...
    "error==positive & rate==positive => u=positive (1)"]);

Visualize the FIS structure.

figure
plotfis(fpid)

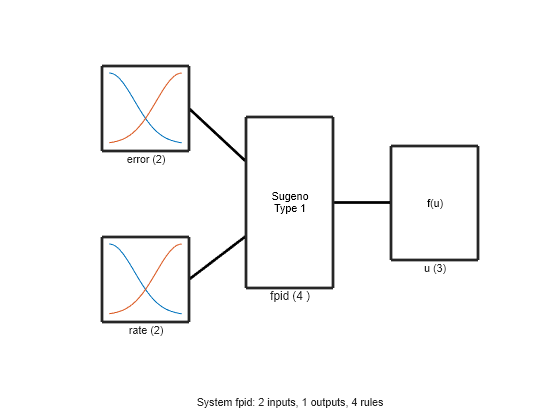
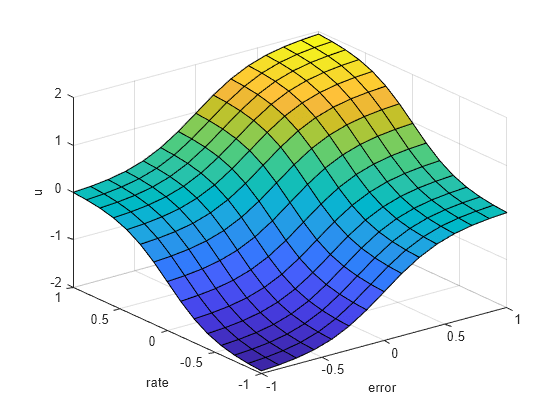
fpid uses the following nonlinear control surface for regulating the power levels of the heater.

figure
gensurf(fpid)

Figure contains an axes object. The axes object with xlabel error, ylabel rate contains an object of type surface.

Comfort Level Simulation Results

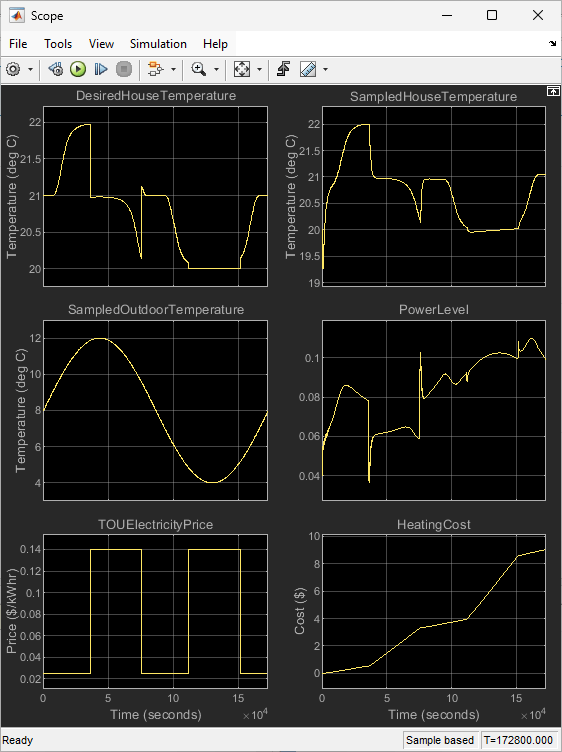
Simulate the model for two days with different comfort levels. For each simulation, the initial room temperature is 20 $°$ C.

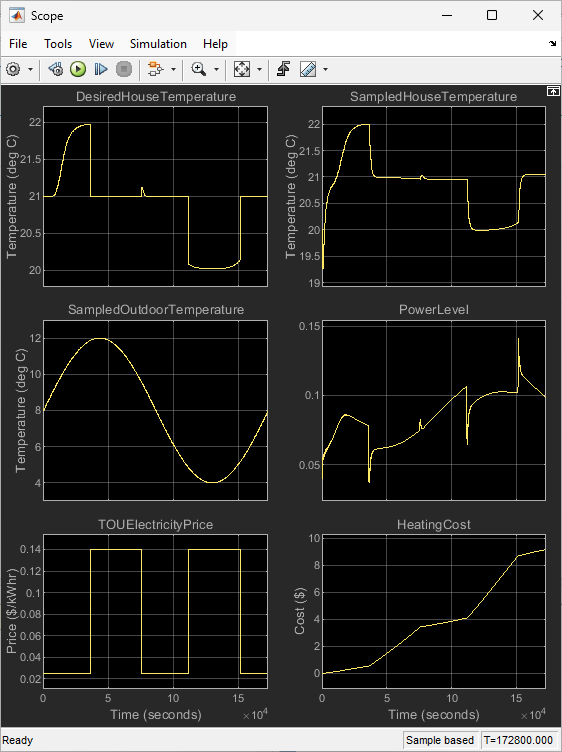
Set the minimum comfort level and simulate the model. The controller maintains a room temperature of 20 $°$ C.

set_param(model+"/Comfort/Level","Value","1")
sim(model)

Set the variable comfort level and simulate the model. The controller adjusts the room temperature within the comfortable zone depending on the outdoor temperature and electricity price.

set_param(model+"/Comfort/Level","Value","2")
sim(model)

Set the maximum comfort level and simulate the model. The controller maintains a room temperature of 22 $°$ C.

set_param(model+"/Comfort/Level","Value","3")
sim(model)

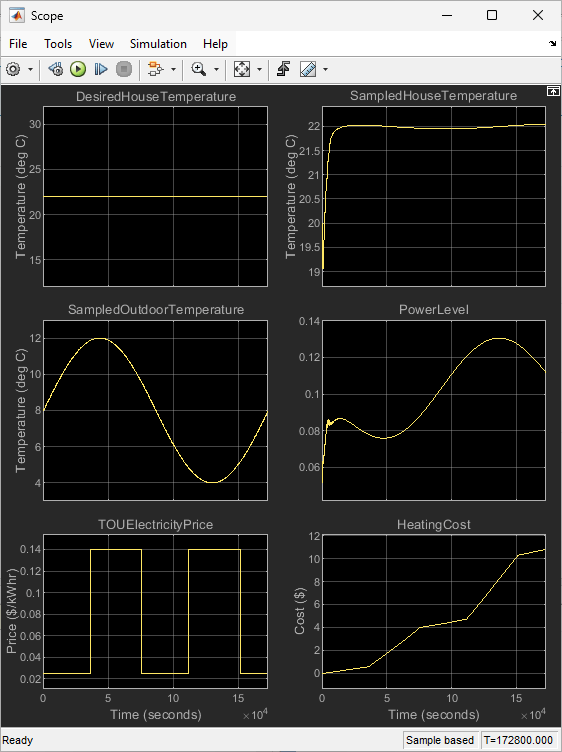
The following table shows the total cost for each comfort level. As expected, the minimum and maximum comfort levels produce the lowest and highest costs, respectively.

The variable comfort level produces a cost between the other two values by balancing the trade-off between cost and comfort.

Comfort Level	Heating Cost ($)
Minimum	8.59
Variable	9.16
Maximum	10.79

Other Control Strategies

By using fuzzy rule bases, FIS-based controller design provides flexible modeling options. For example, you can incorporate the domain expertise of a human operator for solving control or decision-making problems. In this example, the end-user of the heating system can construct a different set of fuzzy rules. For example, they can use a more conservative control approach. For the variable comfort level, change the following rules to set the desired room temperature to low (20 $°$ C) for a low outdoor temperature or high electricity price.

desiredHT.Rules(1).Description = ...
    "Tout==low & elecPrice==low & comfort==varC => Thouse=low (1)";
desiredHT.Rules(5).Description = ...
    "Tout==medium & elecPrice==high & comfort==varC => Thouse=low (1)";
disp([desiredHT.Rules(1:6).Description]')

    "Tout==low & elecPrice==low & comfort==varC => Thouse=low (1)"
    "Tout==medium & elecPrice==low & comfort==varC => Thouse=medium (1)"
    "Tout==high & elecPrice==low & comfort==varC => Thouse=high (1)"
    "Tout==low & elecPrice==high & comfort==varC => Thouse=low (1)"
    "Tout==medium & elecPrice==high & comfort==varC => Thouse=low (1)"
    "Tout==high & elecPrice==high & comfort==varC => Thouse=medium (1)"

View the updated cotnrol surface. The more conservative strategy increases the size of the region where the desired temperature is low.

figure
gensurf(desiredHT)

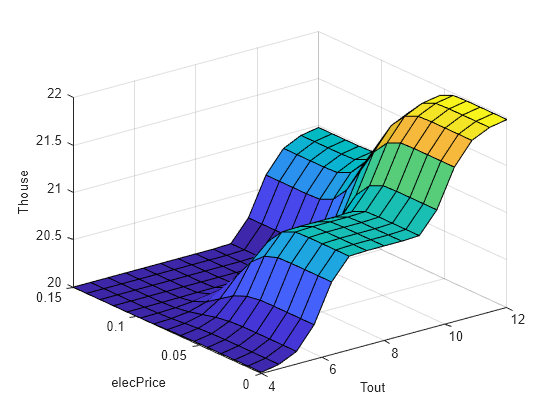
Figure contains an axes object. The axes object with xlabel Tout, ylabel elecPrice contains an object of type surface.

Run the model with the new control strategy. This control strategy produces a lower heating cost ($9.05) compared to the previous variable-comfort cost.

set_param(model+"/Comfort/Level","Value","2")
sim(model)

Conclusion

You can further improve the fuzzy controller by incorporating:

Additional input variables to desiredHT, such as the current room temperature and current power level of the heater to produce smooth transitions between the desired room temperature values.
A FIS tree to hierarchically combine the effects of multiple input variables for determining the desired room temperature values.

You can also include a cooling system for a wider range temperature control under different seasonal outdoor ambient temperature conditions.