比较 paretosearch 和 gamultiobj
此示例显示如何使用 paretosearch 和 gamultiobj 在帕累托前沿上创建一组点。目标函数有两个目标和一个二维控制变量 x。当您点击按钮来编辑或尝试此示例时,目标函数 mymulti3 在您的 MATLAB® 会话中可用。或者,将 mymulti3 代码复制到您的会话。为了提高计算速度,该函数被向量化。
type mymulti3function f = mymulti3(x) % f(:,1) = x(:,1).^4 + x(:,2).^4 + x(:,1).*x(:,2) - (x(:,1).^2).*(x(:,2).^2) - 9*x(:,1).^2; f(:,2) = x(:,2).^4 + x(:,1).^4 + x(:,1).*x(:,2) - (x(:,1).^2).*(x(:,2).^2) + 3*x(:,2).^3;
基本示例和绘图
使用 paretosearch 和 gamultiobj 查找目标函数的帕累托集。将 UseVectorized 选项设置为 true 以提高速度。包括一个绘图函数来可视化帕累托集。
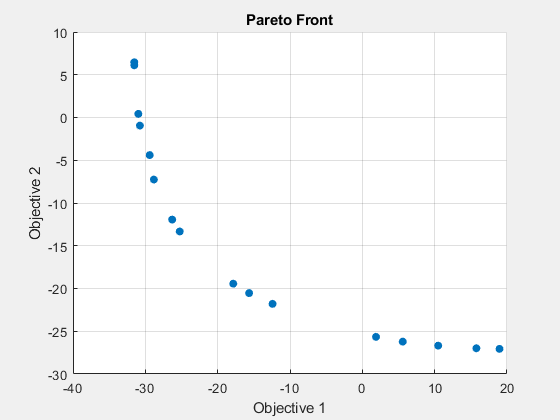
rng default nvars = 2; opts = optimoptions(@gamultiobj,'UseVectorized',true,'PlotFcn','gaplotpareto'); [xga,fvalga,~,gaoutput] = gamultiobj(@(x)mymulti3(x),nvars,[],[],[],[],[],[],[],opts);
gamultiobj stopped because the average change in the spread of Pareto solutions is less than options.FunctionTolerance.
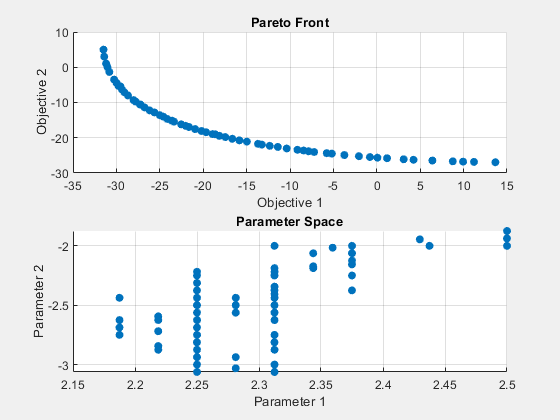
optsp = optimoptions('paretosearch','UseVectorized',true,'PlotFcn',{'psplotparetof' 'psplotparetox'}); [xp,fvalp,~,psoutput] = paretosearch(@(x)mymulti3(x),nvars,[],[],[],[],[],[],[],optsp);
Pareto set found that satisfies the constraints. Optimization completed because the relative change in the volume of the Pareto set is less than 'options.ParetoSetChangeTolerance' and constraints are satisfied to within 'options.ConstraintTolerance'.
使用 mymulti4 计算帕累托前沿上理论上精确的点。当您点击按钮来编辑或尝试此示例时,mymulti4 函数在您的 MATLAB 会话中可用。
type mymulti4function mout = mymulti4(x)
%
gg = [4*x(1)^3+x(2)-2*x(1)*(x(2)^2) - 18*x(1);
x(1)+4*x(2)^3-2*(x(1)^2)*x(2)];
gf = gg + [18*x(1);9*x(2)^2];
mout = gf(1)*gg(2) - gf(2)*gg(1);
mymulti4 函数评估两个目标函数的梯度。接下来,对于 x(2) 的一系列值,使用 fzero 来定位梯度完全平行的点,即输出 mout = 0 的位置。
a = [fzero(@(t)mymulti4([t,-3.15]),[2,3]),-3.15]; for jj = linspace(-3.125,-1.89,50) a = [a;[fzero(@(t)mymulti4([t,jj]),[2,3]),jj]]; end figure plot(fvalp(:,1),fvalp(:,2),'bo'); hold on fs = mymulti3(a); plot(fvalga(:,1),fvalga(:,2),'r*'); plot(fs(:,1),fs(:,2),'k.') legend('Paretosearch','Gamultiobj','True') xlabel('Objective 1') ylabel('Objective 2') hold off

gamultiobj 在目标函数空间中找到分布稍广的点。绘制决策变量空间中的解,以及理论最优帕累托曲线和两个目标函数的轮廓图。
[x,y] = meshgrid(1.9:.01:3.1,-3.2:.01:-1.8); mydata = mymulti3([x(:),y(:)]); myff = sqrt(mydata(:,1) + 39);% Spaces the contours better mygg = sqrt(mydata(:,2) + 28);% Spaces the contours better myff = reshape(myff,size(x)); mygg = reshape(mygg,size(x)); figure; hold on contour(x,y,mygg,50) contour(x,y,myff,50) plot(xp(:,1),xp(:,2),'bo') plot(xga(:,1),xga(:,2),'r*') plot(a(:,1),a(:,2),'-k') xlabel('x(1)') ylabel('x(2)') hold off
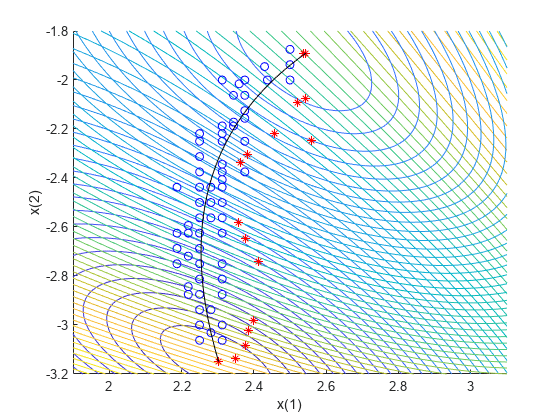
与 paretosearch 解不同,gamultiobj 解在目标函数空间范围的最末端有点。然而,paretosearch 解在目标函数空间和决策变量空间中都有更多更接近真实解的点。当使用默认选项时,每个求解器的帕累托前沿上的点数是不同的。
转移问题
如果问题的解的控制变量很大,会发生什么情况?通过转移问题变量来检查这个案例。对于无约束的问题,gamultiobj 可能会失败,而 paretosearch 对这种转变更具鲁棒性。
为了更容易比较,为每个求解器在帕累托前沿指定 35 个点。
shift = [20,-30];
fun = @(x)mymulti3(x+shift);
opts.PopulationSize = 100; % opts.ParetoFraction = 35
[xgash,fvalgash,~,gashoutput] = gamultiobj(fun,nvars,[],[],[],[],[],[],opts);gamultiobj stopped because the average change in the spread of Pareto solutions is less than options.FunctionTolerance.
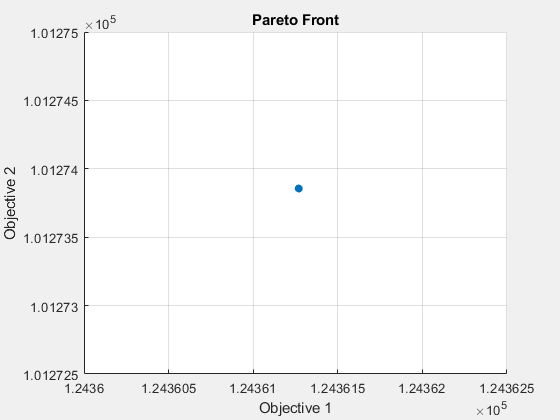
gamultiobj 未能找到有用的帕累托集。
optsp.PlotFcn = []; optsp.ParetoSetSize = 35; [xpsh,fvalpsh,~,pshoutput] = paretosearch(fun,nvars,[],[],[],[],[],[],[],optsp);
Pareto set found that satisfies the constraints. Optimization completed because the relative change in the volume of the Pareto set is less than 'options.ParetoSetChangeTolerance' and constraints are satisfied to within 'options.ConstraintTolerance'.
figure plot(fvalpsh(:,1),fvalpsh(:,2),'bo'); hold on plot(fs(:,1),fs(:,2),'k.') legend('Paretosearch','True') xlabel('Objective 1') ylabel('Objective 2') hold off
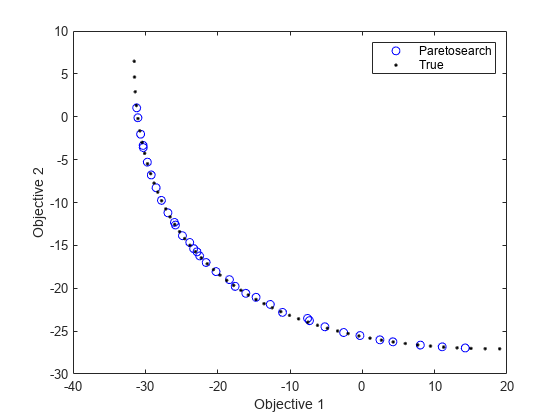
paretosearch 找到均匀分布在几乎整个可能范围内的解点。
添加边界,即使是相当宽松的界限,也有助于 gamultiobj 和 paretosearch 找到适当的解。设置每个分量的 -50 的下界和 50 的上界。
opts.PlotFcn = []; optsp.PlotFcn = []; lb = [-50,-50]; ub = -lb; [xgash,fvalgash,~,gashoutput] = gamultiobj(fun,nvars,[],[],[],[],lb,ub,opts);
gamultiobj stopped because the average change in the spread of Pareto solutions is less than options.FunctionTolerance.
[xpsh2,fvalpsh2,~,pshoutput2] = paretosearch(fun,nvars,[],[],[],[],lb,ub,[],optsp);
Pareto set found that satisfies the constraints. Optimization completed because the relative change in the volume of the Pareto set is less than 'options.ParetoSetChangeTolerance' and constraints are satisfied to within 'options.ConstraintTolerance'.
figure plot(fvalpsh2(:,1),fvalpsh2(:,2),'bo'); hold on plot(fvalgash(:,1),fvalgash(:,2),'r*'); plot(fs(:,1),fs(:,2),'k.') legend('Paretosearch','Gamultiobj','True') xlabel('Objective 1') ylabel('Objective 2') hold off

在这种情况下,两个求解器都找到了良好的解。
从 gamultiobj 解开始 paretosearch
通过从 paretosearch 解开始 gamultiobj,从求解器中获得类似的解范围。
optsp.InitialPoints = xgash; [xpsh3,fvalpsh3,~,pshoutput3] = paretosearch(fun,nvars,[],[],[],[],lb,ub,[],optsp);
Pareto set found that satisfies the constraints. Optimization completed because the relative change in the volume of the Pareto set is less than 'options.ParetoSetChangeTolerance' and constraints are satisfied to within 'options.ConstraintTolerance'.
figure plot(fvalpsh3(:,1),fvalpsh3(:,2),'bo'); hold on plot(fvalgash(:,1),fvalgash(:,2),'r*'); plot(fs(:,1),fs(:,2),'k.') legend('Paretosearch','Gamultiobj','True') xlabel('Objective 1') ylabel('Objective 2') hold off
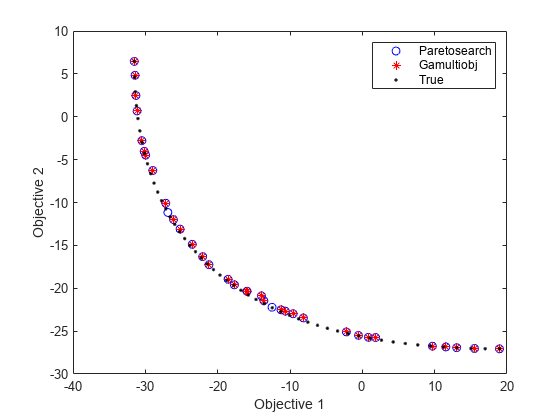
现在 paretosearch 解与 gamultiobj 解类似,尽管某些解点有所不同。
从单目标解开始
获得良好解的另一种方法是从分别最小化每个目标函数的点开始。
从多目标函数中创建一个单目标函数,依次选择每个目标。使用上一节中的移位函数。因为您为求解器提供了良好的起点,所以您不需要指定边界。
nobj = 2; % Number of objectives x0 = -shift; % Initial point for single-objective minimization uncmin = cell(nobj,1); % Cell array to hold the single-objective minima allfuns = zeros(nobj,2); % Hold the objective function values eflag = zeros(nobj,1); fopts = optimoptions('patternsearch','Display','off'); % Use an appropriate solver here for i = 1:nobj indi = zeros(nobj,1); % Choose the objective to minimize indi(i) = 1; funi = @(x)dot(fun(x),indi); [uncmin{i},~,eflag(i)] = patternsearch(funi,x0,[],[],[],[],[],[],[],fopts); % Minimize objective i allfuns(i,:) = fun(uncmin{i}); end uncmin = cell2mat(uncmin); % Matrix of start points
从单目标最小点开始 paretosearch,并注意它的解具有完整范围。paretosearch 将随机初始点添加到所提供的点中,以便拥有至少 options.ParetoSetSize 个体的种群。类似地,gamultiobj 将随机点添加到所提供的点中,以获得至少 (options.PopulationSize)*(options.ParetoFraction) 个体的种群。
optsp = optimoptions(optsp,'InitialPoints',uncmin);
[xpinit,fvalpinit,~,outputpinit] = paretosearch(fun,nvars,[],[],[],[],[],[],[],optsp);Pareto set found that satisfies the constraints. Optimization completed because the relative change in the volume of the Pareto set is less than 'options.ParetoSetChangeTolerance' and constraints are satisfied to within 'options.ConstraintTolerance'.
现在从初始点开始使用 gamultiobj 解决问题。
opts = optimoptions(opts,'InitialPopulationMatrix',uncmin);
[xgash2,fvalgash2,~,gashoutput2] = gamultiobj(fun,nvars,[],[],[],[],[],[],opts);gamultiobj stopped because the average change in the spread of Pareto solutions is less than options.FunctionTolerance.
figure plot(fvalpinit(:,1),fvalpinit(:,2),'bo'); hold on plot(fvalgash2(:,1),fvalgash2(:,2),'r*'); plot(fs(:,1),fs(:,2),'k.') plot(allfuns(:,1),allfuns(:,2),'gs','MarkerSize',12) legend('Paretosearch','Gamultiobj','True','Start Points') xlabel('Objective 1') ylabel('Objective 2') hold off
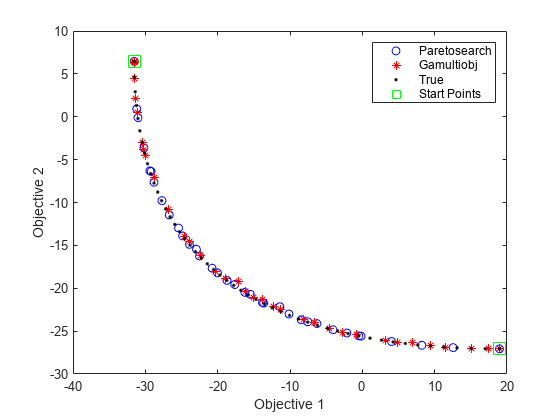
两种求解器均能填充极值点之间的帕累托前沿,并能获得合理准确且间距适当的解。
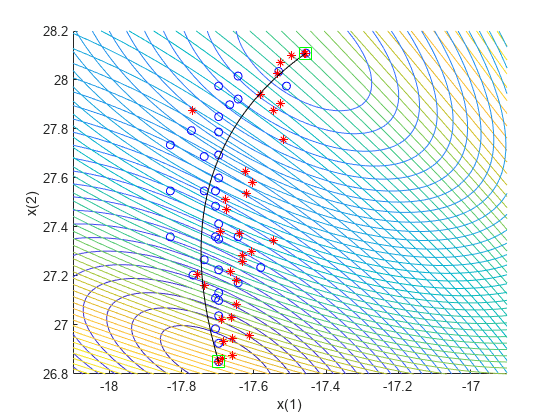
查看决策变量空间中的最终点。
figure; hold on xx = x - shift(1); yy = y - shift(2); contour(xx,yy,mygg,50) contour(xx,yy,myff,50) plot(xpinit(:,1),xpinit(:,2),'bo') plot(xgash2(:,1),xgash2(:,2),'r*') ashift = a - shift; plot(ashift(:,1),ashift(:,2),'-k') plot(uncmin(:,1),uncmin(:,2),'gs','MarkerSize',12); xlabel('x(1)') ylabel('x(2)') hold off