Main Content

本页采用了机器翻译。点击此处可查看最新英文版本。

最小化具有许多局部最小值的函数

打开实时脚本

此示例说明如何使用模拟退火找到函数的局部最小值。该示例介绍了两种最小化方法：在命令行上工作和使用优化实时编辑器任务。

De Jong 第五函数是一个二维函数，具有许多（25）局部极小值。运行此示例时该函数可用。在下图中，不清楚哪一个局部极小值是全局最小值。

dejong5fcn

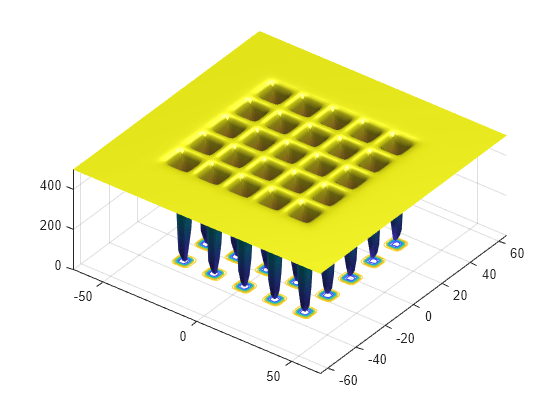
许多标准优化算法陷入了局部极小值。由于模拟退火算法进行广泛的随机搜索，陷入局部最小值的机会减少了。

注意：由于模拟退火使用随机数生成器，因此每次运行该算法时都会得到不同的结果。有关详细信息，请参阅重现结果。

在命令行中最小化

要运行无约束的模拟退火算法，请在命令行中使用 dejong5fcn.m 中的目标函数调用 simulannealbnd，并在以下代码中由匿名函数 @dejong5fcn 引用。

rng(10,'twister') % for reproducibility
fun = @dejong5fcn;
[x,fval] = simulannealbnd(fun,[0 0])
simulannealbnd stopped because the change in best function value is less than options.FunctionTolerance.

x = 1×2

  -16.1292  -15.8214


fval = 6.9034

在结果中：

  • x 是算法返回的最终点。

  • fval 是终点处的目标函数值。

尽量减少使用 Optimize 实时编辑器任务

您还可以使用 优化 实时编辑器任务运行最小化，它提供了一种可视化方法。

  • 点击主页选项卡上文件部分中的新建实时脚本按钮，创建一个新的实时脚本。

new_live_script.png

  • 插入 Optimize 实时编辑器任务。点击插入选项卡，然后在代码部分中选择任务 > 优化。

optimizelet_insert.png

optimizelet_choose.png

  • 单击基于求解器的任务。

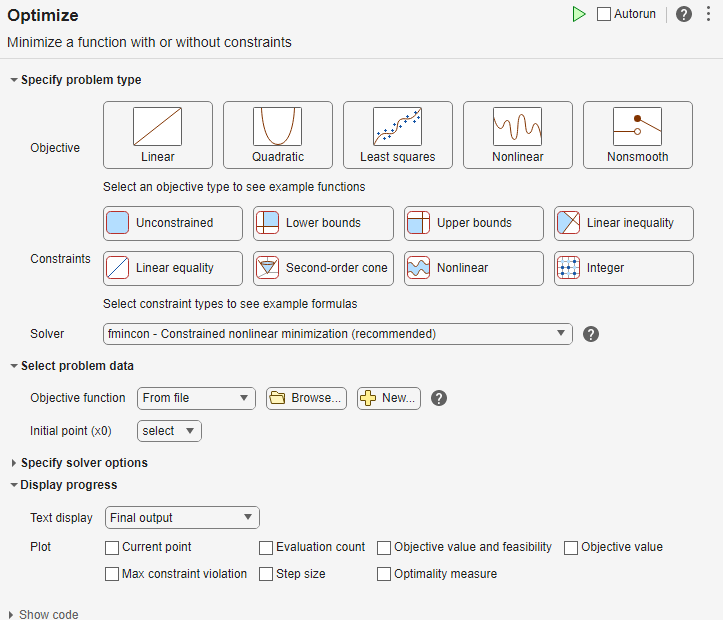
optimizelet_initial.png

  • 为了输入问题数据，请点击插入选项卡上的分节符按钮插入新节。新节出现在任务的上方和下方。

  • 在任务上方的新部分中，输入以下代码来定义初始点和目标函数。

x0 = [0 0];
fun = @dejong5fcn;
rng default % For reproducibility

  • 要将这些变量放入工作区，请按 Ctrl+Enter 运行该部分。

  • 在任务的指定问题类型部分，点击目标 > 非线性按钮。

  • 选择求解器 > simulannealbnd - 模拟退火算法。

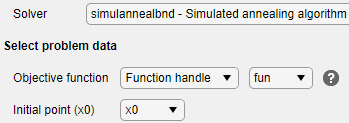
  • 在任务的选择问题数据部分中，选择目标函数> 函数句柄，然后选择 fun。

  • 选择初始点 (x0) > x0。

optimizelet_simulannealbnd_setup.png

  • 在任务的显示进度部分，选择最佳值图。

  • 要运行求解器，请点击任务窗口右上角的选项按钮 ⁝，并选择运行节。绘图出现在单独的图窗窗口中和任务输出区域中。请注意，您的图可能与所示的图不同，因为 simulannealbnd 是一种随机算法。

optimizelet_simulannealbnd_plot.png

  • 要查看解和最佳目标函数值，请查看任务的顶部。

optimizelet_simulannealbnd_solution.png

  • Optimize 实时编辑器任务将名为 solution 和 objectiveValue 的变量返回到工作区。

  • 要查看这些变量的值，请在任务下方的部分输入以下代码。

disp(solution)
disp(objectiveValue)

  • 通过按 Ctrl+Enter 运行该节。

此示例的结尾处有 Optimize 任务处于其最终状态。

Live Task


simulannealbnd stopped because the change in best function value is less than options.FunctionTolerance.

Optimize 实时编辑器任务和命令行都允许您制定和解决问题，并且它们给出相同的结果。命令行更加精简，但对于选择求解器、设置问题以及选择绘图函数等选项提供的帮助较少。您还可以使用 Optimize 开始一个问题，然后生成用于命令行的代码，如 使用优化实时编辑器任务或求解器的有约束非线性问题。

另请参阅

相关主题