使用优化实时编辑器任务或求解器的有约束非线性问题

典型优化问题

此示例说明如何使用 Optimization Toolbox™ 求解器求解有约束非线性问题。该示例展示了典型的工作流：创建目标函数、创建约束、求解问题和检查结果。

此示例提供两种求解问题的方法。一种方法使用优化实时编辑器任务，这是一种可视化方法。另一种方法使用 MATLAB^® 命令行，这是一种基于文本的方法。您也可以使用基于问题的方法来求解这类问题；请参阅基于问题求解有约束非线性问题：。

问题表示：罗森布罗克函数

问题可以表示为在单位圆盘上最小化罗森布罗克函数

$f (x) = 100 {(x_{2} - x_{1}^{2})}^{2} + {(1 - x_{1})}^{2},$

（单位圆盘指以原点为中心、半径为 1 的圆盘）。也就是说，基于数据集 $x_{1}^{2} + x_{2}^{2} \leq 1$ ，求使函数 f(x) 最小的 x。此问题是最小化具有非线性约束的非线性函数。

注意

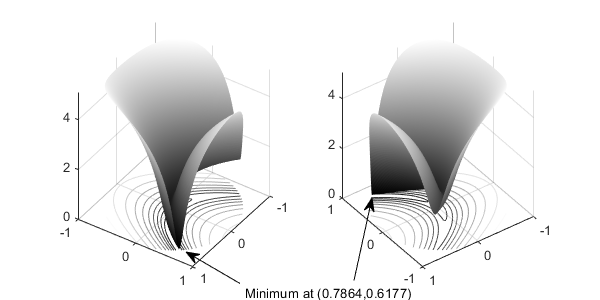
罗森布罗克函数是优化中的标准测试函数。它在点 [1,1] 点达到唯一最小值 0。对于某些算法来说，求最小值是一个挑战，因为函数在深度弯曲的波谷中有一个低浅最小值。此问题的解不在 [1,1] 点处，因为该点不满足约束。

以下图窗显示单位圆盘中罗森布罗克函数的两个视图。垂直轴采用对数刻度；换句话说，绘图显示 log(1+f(x))。等高线位于曲面图下方。

经过对数尺度变换的罗森布罗克函数：两个视图。

The Rosenbrock's function surface plot is steep and has a curve. The underlying level curves are somewhat parabolic.

用于生成图窗的代码

函数 f(x) 称为目标函数。目标函数是您要进行最小化的函数。不等式 $x_{1}^{2} + x_{2}^{2} \leq 1$ 称为约束。约束限制求解器用于搜索最小值的 x 集。您可以使用任意数量的约束，约束可以是不等式，也可以是等式。

所有 Optimization Toolbox 优化函数都可用于最小化目标函数。要最大化函数 f，请应用优化例程来最小化 –f。有关最大化的详细信息，请参阅对目标进行最大化。

使用优化实时编辑器任务定义和求解问题

优化实时编辑器任务允许您使用可视化方法设置和求解问题。

点击主页选项卡文件部分的新建实时脚本按钮，创建一个新的实时脚本。
插入一个优化实时编辑器任务。点击插入选项卡，然后在代码部分中选择任务 > 优化。
选择基于求解器的任务。
在任务的指定问题类型节中，选择目标 > 非线性和约束 > 非线性。该任务选择求解器 fmincon - 有约束非线性最小化。

包括罗森布罗克函数作为目标函数。在任务的选择问题数据节中，选择目标函数 > 局部函数，然后点击新建... 按钮。新局部函数出现在任务下的一个节中。

function f = objectiveFcn(optimInput)
% Example:
% Minimize Rosenbrock's function
% f = 100*(y - x^2)^2 + (1 - x)^2

% Edit the lines below with your calculation
x = optimInput(1);
y = optimInput(2);
f = 100*(y - x^2)^2 + (1 - x)^2;
end

此函数实现罗森布罗克函数。

在任务的选择问题数据节中，选择目标函数 > objectiveFcn。
将初始点 x0 = [0;0] 放入 MATLAB 工作区中。通过点击任务，然后点击插入选项卡上的分节符按钮，在优化任务上方插入一个新节。在任务上方的新节中，输入以下初始点代码。
```
x0 = [0;0];
```
通过按 Ctrl+Enter 运行该节。此操作会将 x0 放入工作区中。
在任务的选择问题数据节中，选择初始点(x0) > x0。
在选择问题数据节中，选择约束 > 非线性 > 局部函数，然后点击新建... 按钮。新局部函数出现在前一个局部函数的下方。

按如下所示编辑新局部函数。

function [c,ceq] = unitdisk(x)
c = x(1)^2 + x(2)^2 - 1;
ceq = [ ];
end

在选择问题数据节中，选择 unitdisk 作为约束函数。
要监控求解器进度，请在任务的显示进度节中，选择文本显示 > 每次迭代。此外，为绘图选择目标值和可行性。
要运行求解器，请点击任务窗口右上角的选项按钮 ⁝，并选择运行节。绘图出现在单独的图窗窗口中和输出区域中。
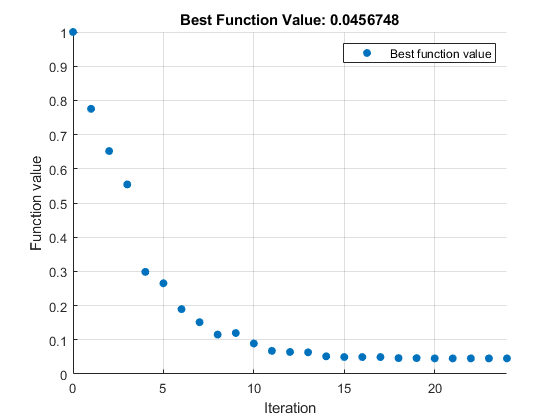
输出区域显示一个迭代表，解释结果中有对它的进一步说明。
要找到解，请查看任务的顶部。
求解器将变量 solution 和 objectiveValue 放置在工作区中。通过在任务下方插入新分节符并输入以下行来查看其值。
通过按 Ctrl+Enter 运行该节。
要了解 fmincon 得到结果的过程，请参阅解释结果。
要显示优化为求解问题而生成的代码，请点击任务窗口右上角的选项按钮 ⁝，并选择控件和代码。
在任务的底部，出现以下代码。
```
% Set nondefault solver options
options = optimoptions('fmincon','Display','iter','PlotFcn',...
    'optimplotfvalconstr');

% Solve
[solution,objectiveValue] = fmincon(@objectiveFcn,x0,[],[],[],[],[],[],...
    @unitdisk,options);
```
此代码是您在命令行中用于求解问题的代码，如下节中所述。

在命令行中定义和求解问题

在命令行中求解优化问题的第一步是选择求解器。请查阅优化决策表。对于具有非线性目标函数和非线性约束的问题，通常使用 fmincon 求解器。

请查阅 fmincon 函数参考页。求解器语法如下。

[x,fval] = fmincon(fun,x0,A,b,Aeq,beq,lb,ub,nonlcon,options)

fun 和 nonlcon 输入分别表示目标函数和非线性约束函数。

以如下方式表达您的问题：

以 MATLAB 语言将目标函数定义为函数文件或匿名函数。此示例使用一个函数文件。
将约束定义为一个单独的文件或匿名函数。

函数文件是包含 MATLAB 命令的文本文件，扩展名为 .m。在任何文本编辑器中创建函数文件，或像此示例中一样使用内置的 MATLAB 编辑器。

在命令行中输入：
```
edit rosenbrock
```

在 MATLAB 编辑器中输入：

%% ROSENBROCK(x) expects a two-column matrix and returns a column vector
% The output is the Rosenbrock function, which has a minimum at
% (1,1) of value 0, and is strictly positive everywhere else.

function f = rosenbrock(x)

f = 100*(x(:,2) - x(:,1).^2).^2 + (1 - x(:,1)).^2;

注意

rosenbrock 是向量化函数，它可以一次计算多个点处的值。请参阅向量化。向量化函数最适合绘图。对于非向量化版本，请输入：

%% ROSENBROCK1(x) expects a two-element vector and returns a scalar
% The output is the Rosenbrock function, which has a minimum at
% (1,1) of value 0, and is strictly positive everywhere else.

function f = rosenbrock1(x)

f = 100*(x(2) - x(1)^2)^2 + (1 - x(1))^2;

用名称 rosenbrock.m 保存文件。

约束函数的形式为 c(x) ≤ 0 或 ceq(x) = 0.约束 $x_{1}^{2} + x_{2}^{2} \leq 1$ 未采用求解器处理的形式。要使用正确的语法，请将约束重新表示为 $x_{1}^{2} + x_{2}^{2} - 1 \leq 0$ 。

非线性约束的语法会同时返回等式和不等式约束。此示例仅包含一个不等式约束，因此您必须将空数组 [] 作为等式约束函数 ceq 进行传递。

考虑到这些因素，为非线性约束编写一个函数文件。

创建一个名为 unitdisk.m 的文件，其中包含以下代码：

function [c,ceq] = unitdisk(x)
c = x(1)^2 + x(2)^2 - 1;
ceq = [ ];

保存 unitdisk.m 文件。
创建目标函数和约束函数的函数句柄。这些函数句柄指向函数，是求解器访问函数的一种方式。
```
fun = @rosenbrock;
nonlcon = @unitdisk;
```

现在您已定义了目标函数和约束函数，接着创建其他 fmincon 输入。

为 fmincon 创建选项，以使用 'optimplotfvalconstr' 绘图函数并返回迭代输出。

options = optimoptions('fmincon',...
    'PlotFcn','optimplotfvalconstr',...
    'Display','iter');

创建初始点。
```
x0 = [0 0];
```

为此示例不使用的约束创建空项。

A = [];
b = [];
Aeq = [];
beq = [];
lb = [];
ub = [];

通过调用 fmincon 求解问题。

[x,fval] = fmincon(fun,x0,A,b,Aeq,beq,lb,ub,nonlcon,options)

                                            First-order      Norm of
 Iter F-count            f(x)  Feasibility   optimality         step
    0       3    1.000000e+00    0.000e+00    2.000e+00
    1      13    7.753537e-01    0.000e+00    6.250e+00    1.768e-01
    2      18    6.519648e-01    0.000e+00    9.048e+00    1.679e-01
    3      21    5.543209e-01    0.000e+00    8.033e+00    1.203e-01
    4      24    2.985207e-01    0.000e+00    1.790e+00    9.328e-02
    5      27    2.653799e-01    0.000e+00    2.788e+00    5.723e-02
    6      30    1.897216e-01    0.000e+00    2.311e+00    1.147e-01
    7      33    1.513701e-01    0.000e+00    9.706e-01    5.764e-02
    8      36    1.153330e-01    0.000e+00    1.127e+00    8.169e-02
    9      39    1.198058e-01    0.000e+00    1.000e-01    1.522e-02
   10      42    8.910052e-02    0.000e+00    8.378e-01    8.301e-02
   11      45    6.771960e-02    0.000e+00    1.365e+00    7.149e-02
   12      48    6.437664e-02    0.000e+00    1.146e-01    5.701e-03
   13      51    6.329037e-02    0.000e+00    1.883e-02    3.774e-03
   14      54    5.161934e-02    0.000e+00    3.016e-01    4.464e-02
   15      57    4.964194e-02    0.000e+00    7.913e-02    7.894e-03
   16      60    4.955404e-02    0.000e+00    5.462e-03    4.185e-04
   17      63    4.954839e-02    0.000e+00    3.993e-03    2.208e-05
   18      66    4.658289e-02    0.000e+00    1.318e-02    1.255e-02
   19      69    4.647011e-02    0.000e+00    8.006e-04    4.940e-04
   20      72    4.569141e-02    0.000e+00    3.136e-03    3.379e-03
   21      75    4.568281e-02    0.000e+00    6.440e-05    3.974e-05
   22      78    4.568281e-02    0.000e+00    8.000e-06    1.084e-07
   23      81    4.567641e-02    0.000e+00    1.601e-06    2.793e-05
   24      84    4.567482e-02    0.000e+00    2.023e-08    6.916e-06

Local minimum found that satisfies the constraints.

Optimization completed because the objective function is non-decreasing in 
feasible directions, to within the value of the optimality tolerance,
and constraints are satisfied to within the value of the constraint tolerance.

x =

    0.7864    0.6177


fval =

    0.0457

Function values generally decrease as iterations proceed

退出消息指出，由于目标函数在约束允许方向上的导数接近 0，因此对约束下的最优值的搜索结束，并且解在要求的准确度内满足约束。消息中有一些语句包含指向所用词语的详细信息链接。有关这些链接的详细信息，请参阅增强版退出消息。

解释结果

实时编辑器任务输出区域和 MATLAB 命令行窗口中的迭代表显示 MATLAB 如何在单位圆盘中搜索罗森布罗克函数的最小值。根据您使用的工具箱版本和计算平台的不同，该表可能有所不同。以下说明适用于此示例中显示的表。

第一列（标记为 Iter）是从 0 到 24 的迭代序号。fmincon 经过 24 次迭代后收敛。
第二列（标记为 F-count）报告计算罗森布罗克函数的累计次数。最后一行显示 F-count 为 84，表明 fmincon 在求解最小值的过程中对罗森布罗克函数进行了 84 次计算。
第三列（标记为 f(x)）显示目标函数值。最终值 4.567482e-2 是在优化运行中报告的最小值，位于命令行窗口中退出消息的末尾。
第四列 Feasibility 对于所有迭代均为 0。此列显示在约束为正的每次迭代中约束函数 unitdisk 的值。由于 unitdisk 的值在所有迭代中均为负数，因此每次迭代都满足约束。

迭代表的其他列在迭代输出中有说明。

另请参阅

fmincon | 优化