fmincon
寻找约束非线性多变量函数的最小值
语法
说明
非线性规划求解器。
求以下问题的最小值:
b 和 beq 是向量,A 和 Aeq 是矩阵,c(x) 和 ceq(x) 是返回向量的函数,f(x) 是返回标量的函数。f(x)、c(x) 和 ceq(x) 可以是非线性函数。
x、lb 和 ub 可以作为向量或矩阵传递;请参阅矩阵参量。
x = fmincon(fun,x0,A,b,Aeq,beq,lb,ub)x 中的设计变量定义一组下界和上界,使解始终在 lb ≤ x ≤ ub 范围内。如果不存在等式,请设置 Aeq = [] 和 beq = []。如果 x(i) 无下界,请设置 lb(i) = -Inf,如果 x(i) 无上界,请设置 ub(i) = Inf。
注意
如果为问题指定的输入边界不一致,fmincon 会抛出错误。这种情况下,输出 x 为 x0,fval 为 []。
对于默认的 'interior-point' 算法,fmincon 将违反边界 lb ≤ x ≤ ub 或等于某一边界的 x0 分量重置到边界区域内部。对于 'trust-region-reflective' 算法,fmincon 将违反边界的分量重置到边界区域内部。对于其他算法,fmincon 将违反边界的分量重置为最近边界的值。遵守边界的分量不会更改。请参阅迭代可能违反约束。
示例
在具有线性不等式约束的情况下求罗森布罗克函数的最小值。
将目标函数 fun 设置为罗森布罗克函数。众所周知,Rosenbrock 函数很难实现最小化。它在点 (1,1) 处的最小目标值为 0。有关详细信息,请参阅使用优化实时编辑器任务或求解器的有约束非线性问题。
fun = @(x)100*(x(2)-x(1)^2)^2 + (1-x(1))^2;
从点 [-1,2] 开始求最小值,约束为 。以 A = [1,2] 和 b = 1 为条件,以 Ax <= b 形式表达此约束。请注意,此约束意味着解不会在无约束解 (1,1) 处,因为在此点处 。
x0 = [-1,2]; A = [1,2]; b = 1; x = fmincon(fun,x0,A,b)
Local minimum found that satisfies the constraints. Optimization completed because the objective function is non-decreasing in feasible directions, to within the value of the optimality tolerance, and constraints are satisfied to within the value of the constraint tolerance. <stopping criteria details>
x = 1×2
0.5022 0.2489
在既有线性不等式约束又有线性等式约束的情况下求罗森布罗克函数的最小值。
将目标函数 fun 设置为罗森布罗克函数。
fun = @(x)100*(x(2)-x(1)^2)^2 + (1-x(1))^2;
从点 [0.5,0] 开始求最小值,约束为 和 。
以
A = [1,2]和b = 1为条件,以A*x <= b形式表达线性不等式约束。以
Aeq = [2,1]和beq = 1为条件,以Aeq*x = beq形式表达线性等式约束。
x0 = [0.5,0]; A = [1,2]; b = 1; Aeq = [2,1]; beq = 1; x = fmincon(fun,x0,A,b,Aeq,beq)
Local minimum found that satisfies the constraints. Optimization completed because the objective function is non-decreasing in feasible directions, to within the value of the optimality tolerance, and constraints are satisfied to within the value of the constraint tolerance. <stopping criteria details>
x = 1×2
0.4149 0.1701
在存在边界约束的情况下,求目标函数的最小值。
目标函数是具有两个变量的简单代数函数。
fun = @(x)1+x(1)/(1+x(2)) - 3*x(1)*x(2) + x(2)*(1+x(1));
关注 为正值且满足 和 的区域。
lb = [0,0]; ub = [1,2];
该问题没有线性约束,因此将这些参量设置为 []。
A = []; b = []; Aeq = []; beq = [];
尝试使用一个位于区域中部的初始点。
x0 = (lb + ub)/2;
求解。
x = fmincon(fun,x0,A,b,Aeq,beq,lb,ub)
Local minimum found that satisfies the constraints. Optimization completed because the objective function is non-decreasing in feasible directions, to within the value of the optimality tolerance, and constraints are satisfied to within the value of the constraint tolerance. <stopping criteria details>
x = 1×2
1.0000 2.0000
使用另一个初始点会得到不同的解。
x0 = x0/5; x = fmincon(fun,x0,A,b,Aeq,beq,lb,ub)
Local minimum found that satisfies the constraints. Optimization completed because the objective function is non-decreasing in feasible directions, to within the value of the optimality tolerance, and constraints are satisfied to within the value of the constraint tolerance. <stopping criteria details>
x = 1×2
10-6 ×
0.4000 0.4000
要确定哪个解更好,请参阅获得目标函数值。
在非线性约束下求函数的最小值
在边界约束下求罗森布罗克函数在圆内最小的点。
fun = @(x)100*(x(2)-x(1)^2)^2 + (1-x(1))^2;
在区域 、 内寻找。
lb = [0,0.2]; ub = [0.5,0.8];
同时在以 [1/3,1/3] 为圆心、半径为 1/3 的圆内寻找。将此代码用于非线性约束函数。
function [c,ceq] = circlecon(x) c = (x(1)-1/3)^2 + (x(2)-1/3)^2 - (1/3)^2; ceq = []; end
没有线性约束,因此将这些参量设置为 []。
A = []; b = []; Aeq = []; beq = [];
选择一个满足所有约束的初始点。
x0 = [1/4,1/4];
求解。
nonlcon = @circlecon; x = fmincon(fun,x0,A,b,Aeq,beq,lb,ub,nonlcon)
Local minimum found that satisfies the constraints. Optimization completed because the objective function is non-decreasing in feasible directions, to within the value of the optimality tolerance, and constraints are satisfied to within the value of the constraint tolerance. <stopping criteria details>
x = 1×2
0.5000 0.2500
设置选项以在迭代期间查看输出信息并使用不同算法。
要观察 fmincon 求解过程,请将 Display 选项设置为 'iter'。此外,尝试 'sqp' 算法,该算法有时比默认的 'interior-point' 算法更快或更准确。
options = optimoptions('fmincon','Display','iter','Algorithm','sqp');
在单位圆盘 上求罗森布罗克函数的最小值。首先创建一个表示非线性约束的函数。将此函数保存为 MATLAB® 路径上名为 unitdisk.m 的文件。
type unitdisk.mfunction [c,ceq] = unitdisk(x) c = x(1)^2 + x(2)^2 - 1; ceq = [];
创建其余的问题设定。然后运行 fmincon。
fun = @(x)100*(x(2)-x(1)^2)^2 + (1-x(1))^2; A = []; b = []; Aeq = []; beq = []; lb = []; ub = []; nonlcon = @unitdisk; x0 = [0,0]; x = fmincon(fun,x0,A,b,Aeq,beq,lb,ub,nonlcon,options)
Iter Func-count Fval Feasibility Step Length Norm of First-order
step optimality
0 3 1.000000e+00 0.000e+00 1.000e+00 0.000e+00 2.000e+00
1 12 8.913011e-01 0.000e+00 1.176e-01 2.353e-01 1.107e+01
2 22 8.047847e-01 0.000e+00 8.235e-02 1.900e-01 1.330e+01
3 28 4.197517e-01 0.000e+00 3.430e-01 1.217e-01 6.172e+00
4 31 2.733703e-01 0.000e+00 1.000e+00 5.254e-02 5.705e-01
5 34 2.397111e-01 0.000e+00 1.000e+00 7.498e-02 3.164e+00
6 37 2.036002e-01 0.000e+00 1.000e+00 5.960e-02 3.106e+00
7 40 1.164353e-01 0.000e+00 1.000e+00 1.459e-01 1.059e+00
8 43 1.161753e-01 0.000e+00 1.000e+00 1.754e-01 7.383e+00
9 46 5.901601e-02 0.000e+00 1.000e+00 1.547e-02 7.278e-01
10 49 4.533081e-02 2.898e-03 1.000e+00 5.393e-02 1.252e-01
11 52 4.567454e-02 2.225e-06 1.000e+00 1.492e-03 1.679e-03
12 55 4.567481e-02 4.406e-12 1.000e+00 2.095e-06 1.501e-05
13 58 4.567481e-02 0.000e+00 1.000e+00 2.159e-09 1.511e-05
Local minimum possible. Constraints satisfied.
fmincon stopped because the size of the current step is less than
the value of the step size tolerance and constraints are
satisfied to within the value of the constraint tolerance.
<stopping criteria details>
x = 1×2
0.7864 0.6177
有关迭代输出的详细信息,请参阅迭代输出。
将梯度计算加入目标函数中,以实现更快或更可靠的计算。
将梯度计算作为条件化输出包含在目标函数文件中。有关详细信息,请参阅包括梯度和黑塞函数。目标函数是罗森布罗克函数,
它有梯度
此代码创建了 rosenbrockwithgrad 函数,该函数使用梯度实现目标函数。
function [f,g] = rosenbrockwithgrad(x) % Calculate objective f f = 100*(x(2) - x(1)^2)^2 + (1-x(1))^2; if nargout > 1 % gradient required g = [-400*(x(2)-x(1)^2)*x(1)-2*(1-x(1)); 200*(x(2)-x(1)^2)]; end end
创建使用目标函数梯度的选项。
options = optimoptions('fmincon','SpecifyObjectiveGradient',true);
为问题创建其他输入。然后调用 fmincon。
fun = @rosenbrockwithgrad; x0 = [-1,2]; A = []; b = []; Aeq = []; beq = []; lb = [-2,-2]; ub = [2,2]; nonlcon = []; x = fmincon(fun,x0,A,b,Aeq,beq,lb,ub,nonlcon,options)
Local minimum found that satisfies the constraints. Optimization completed because the objective function is non-decreasing in feasible directions, to within the value of the optimality tolerance, and constraints are satisfied to within the value of the constraint tolerance. <stopping criteria details>
x = 1×2
1.0000 1.0000
使用问题结构体而不是单独的参量来求解与非默认选项中相同的问题。
创建选项以及一个问题结构体。有关字段名称和必需的字段,请参阅problem。
options = optimoptions('fmincon','Display','iter','Algorithm','sqp'); problem.options = options; problem.solver = 'fmincon'; problem.objective = @(x)100*(x(2)-x(1)^2)^2 + (1-x(1))^2; problem.x0 = [0,0];
非线性约束函数 unitdisk 出现在此示例末尾。在 problem 中包含该非线性约束函数。
problem.nonlcon = @unitdisk;
求解。
x = fmincon(problem)
Iter Func-count Fval Feasibility Step Length Norm of First-order
step optimality
0 3 1.000000e+00 0.000e+00 1.000e+00 0.000e+00 2.000e+00
1 12 8.913011e-01 0.000e+00 1.176e-01 2.353e-01 1.107e+01
2 22 8.047847e-01 0.000e+00 8.235e-02 1.900e-01 1.330e+01
3 28 4.197517e-01 0.000e+00 3.430e-01 1.217e-01 6.172e+00
4 31 2.733703e-01 0.000e+00 1.000e+00 5.254e-02 5.705e-01
5 34 2.397111e-01 0.000e+00 1.000e+00 7.498e-02 3.164e+00
6 37 2.036002e-01 0.000e+00 1.000e+00 5.960e-02 3.106e+00
7 40 1.164353e-01 0.000e+00 1.000e+00 1.459e-01 1.059e+00
8 43 1.161753e-01 0.000e+00 1.000e+00 1.754e-01 7.383e+00
9 46 5.901602e-02 0.000e+00 1.000e+00 1.547e-02 7.278e-01
10 49 4.533081e-02 2.898e-03 1.000e+00 5.393e-02 1.252e-01
11 52 4.567454e-02 2.225e-06 1.000e+00 1.492e-03 1.679e-03
12 55 4.567481e-02 4.386e-12 1.000e+00 2.095e-06 1.502e-05
13 58 4.567481e-02 0.000e+00 1.000e+00 2.193e-12 1.406e-05
Local minimum possible. Constraints satisfied.
fmincon stopped because the size of the current step is less than
the value of the step size tolerance and constraints are
satisfied to within the value of the constraint tolerance.
<stopping criteria details>
x = 1×2
0.7864 0.6177
迭代输出和解与在非默认选项中的相同。
以下代码创建 unitdisk 函数。
function [c,ceq] = unitdisk(x) c = x(1)^2 + x(2)^2 - 1; ceq = []; end
带 fval 输出调用 fmincon,以获得解处的目标函数值。
存在边界约束进行最小化示例给出了两个解。哪个更好?运行以下示例,它请求 fval 输出和解。
fun = @(x)1+x(1)./(1+x(2)) - 3*x(1).*x(2) + x(2).*(1+x(1)); lb = [0,0]; ub = [1,2]; A = []; b = []; Aeq = []; beq = []; x0 = (lb + ub)/2; [x,fval] = fmincon(fun,x0,A,b,Aeq,beq,lb,ub)
Local minimum found that satisfies the constraints. Optimization completed because the objective function is non-decreasing in feasible directions, to within the value of the optimality tolerance, and constraints are satisfied to within the value of the constraint tolerance. <stopping criteria details>
x = 1×2
1.0000 2.0000
fval = -0.6667
使用另一个起点 x0 运行问题。
x0 = x0/5; [x2,fval2] = fmincon(fun,x0,A,b,Aeq,beq,lb,ub)
Local minimum found that satisfies the constraints. Optimization completed because the objective function is non-decreasing in feasible directions, to within the value of the optimality tolerance, and constraints are satisfied to within the value of the constraint tolerance. <stopping criteria details>
x2 = 1×2
10-6 ×
0.4000 0.4000
fval2 = 1.0000
此解的目标函数值 fval2 = 1,高于第一个值 fval = –0.6667。第一个解 x 具有较低的目标函数局部最小值。
要轻松检查解的质量,可请求 exitflag 和 output 输出。
设立一个在单位圆盘  上最小化罗森布罗克函数的问题。首先创建一个表示非线性约束的函数。将此函数保存为 MATLAB® 路径上名为
上最小化罗森布罗克函数的问题。首先创建一个表示非线性约束的函数。将此函数保存为 MATLAB® 路径上名为 unitdisk.m 的文件。
function [c,ceq] = unitdisk(x)
c = x(1)^2 + x(2)^2 - 1;
ceq = [];
创建其余的问题设定。
fun = @(x)100*(x(2)-x(1)^2)^2 + (1-x(1))^2; nonlcon = @unitdisk; A = []; b = []; Aeq = []; beq = []; lb = []; ub = []; x0 = [0,0];
使用 fval、exitflag 和 output 输出调用 fmincon。
[x,fval,exitflag,output] = fmincon(fun,x0,A,b,Aeq,beq,lb,ub,nonlcon)
Local minimum found that satisfies the constraints.
Optimization completed because the objective function is non-decreasing in
feasible directions, to within the value of the optimality tolerance,
and constraints are satisfied to within the value of the constraint tolerance.
x =
0.7864 0.6177
fval =
0.0457
exitflag =
1
output =
struct with fields:
iterations: 24
funcCount: 84
constrviolation: 0
stepsize: 6.9162e-06
algorithm: 'interior-point'
firstorderopt: 2.4373e-08
cgiterations: 4
message: 'Local minimum found that satisfies the constraints.↵↵Optimization completed because the objective function is non-decreasing in ↵feasible directions, to within the value of the optimality tolerance,↵and constraints are satisfied to within the value of the constraint tolerance.↵↵<stopping criteria details>↵↵Optimization completed: The relative first-order optimality measure, 2.437331e-08,↵is less than options.OptimalityTolerance = 1.000000e-06, and the relative maximum constraint↵violation, 0.000000e+00, is less than options.ConstraintTolerance = 1.000000e-06.'
bestfeasible: [1×1 struct]
exitflag值1表示该解是局部最小值。output结构体报告有关求解过程的几个统计量。具体来说,它在output.iterations中给出迭代次数,在output.funcCount中给出函数计算次数,以及在output.constrviolation中给出可行性。
fmincon 可以返回几个输出,您可以使用这些输出来分析报告的解。
设立一个在单位圆盘上最小化罗森布罗克函数的问题。首先创建一个表示非线性约束的函数。将此函数保存为 MATLAB® 路径上名为 unitdisk.m 的文件。
function [c,ceq] = unitdisk(x)
c = x(1)^2 + x(2)^2 - 1;
ceq = [];
创建其余的问题设定。
fun = @(x)100*(x(2)-x(1)^2)^2 + (1-x(1))^2; nonlcon = @unitdisk; A = []; b = []; Aeq = []; beq = []; lb = []; ub = []; x0 = [0,0];
请求所有 fmincon 输出。
[x,fval,exitflag,output,lambda,grad,hessian] = fmincon(fun,x0,A,b,Aeq,beq,lb,ub,nonlcon)
Local minimum found that satisfies the constraints.
Optimization completed because the objective function is non-decreasing in
feasible directions, to within the value of the optimality tolerance,
and constraints are satisfied to within the value of the constraint tolerance.
x =
0.7864 0.6177
fval =
0.0457
exitflag =
1
output =
struct with fields:
iterations: 24
funcCount: 84
constrviolation: 0
stepsize: 6.9162e-06
algorithm: 'interior-point'
firstorderopt: 2.4373e-08
cgiterations: 4
message: 'Local minimum found that satisfies the constraints.↵↵Optimization completed because the objective function is non-decreasing in ↵feasible directions, to within the value of the optimality tolerance,↵and constraints are satisfied to within the value of the constraint tolerance.↵↵<stopping criteria details>↵↵Optimization completed: The relative first-order optimality measure, 2.437331e-08,↵is less than options.OptimalityTolerance = 1.000000e-06, and the relative maximum constraint↵violation, 0.000000e+00, is less than options.ConstraintTolerance = 1.000000e-06.'
bestfeasible: [1×1 struct]
lambda =
struct with fields:
eqlin: [0×1 double]
eqnonlin: [0×1 double]
ineqlin: [0×1 double]
lower: [2×1 double]
upper: [2×1 double]
ineqnonlin: 0.1215
grad =
-0.1911
-0.1501
hessian =
497.2903 -314.5589
-314.5589 200.2392
lambda.ineqnonlin输出显示非线性约束在解处为活动状态,并给出相关联的拉格朗日乘数的值。grad输出给出了在解x处目标函数梯度的值。fmincon黑塞函数 中描述了
hessian输出。
输入参数
要最小化的函数,指定为函数句柄或函数名称。fun 函数接受向量或数组 x,并返回实数标量 f,即在 x 处计算的目标函数值。
fmincon 以 x0 参量的形状将 x 传递给目标函数和任何非线性约束函数。例如,如果 x0 是 5×3 数组,则 fmincon 将 x 以 5×3 数组的形式传递给 fun。但是,在将 x 转换为列向量 x(:) 后,fmincon 会将线性约束矩阵 A 或 Aeq 乘以 x。
将 fun 指定为文件的函数句柄:
x = fmincon(@myfun,x0,A,b)
其中 myfun 是一个 MATLAB® 函数,例如
function f = myfun(x) f = ... % Compute function value at x
您还可以为匿名函数指定 fun 作为函数句柄:
x = fmincon(@(x)norm(x)^2,x0,A,b);
如果您可以计算 fun 的梯度且 SpecifyObjectiveGradient 选项设置为 true,设置如下
options = optimoptions('fmincon','SpecifyObjectiveGradient',true)
fun 必须在第二个输出参量中返回梯度向量 g(x)。如果您还可以计算黑塞矩阵,并通过 optimoptions 将 HessianFcn 选项设置为 'objective',且将 Algorithm 选项设置为 'trust-region-reflective',则 fun 必须在第三个输出参量中返回黑塞函数值 H(x),它是一个对称矩阵。fun 可以给出稀疏黑塞矩阵。有关详细信息,请参阅适用于 fminunc 信赖域或 fmincon 信赖域反射算法的黑塞函数。
如果您还可以计算黑塞矩阵,并且 Algorithm 选项设置为 'interior-point',则有另一种方法将黑塞矩阵传递给 fmincon。有关详细信息,请参阅适用于 fmincon 内点算法的黑塞函数。有关使用 Symbolic Math Toolbox™ 计算梯度和黑塞矩阵的示例,请参阅使用 Symbolic Math Toolbox 计算梯度和 Hessian。
interior-point 和 trust-region-reflective 算法允许您提供黑塞矩阵乘法函数。此函数给出黑塞乘以向量的乘积结果,而不直接计算黑塞矩阵。这可以节省内存。请参阅黑塞矩阵乘法函数。
示例: fun = @(x)sin(x(1))*cos(x(2))
数据类型: char | function_handle | string
数据类型: double
线性不等式约束,指定为实矩阵。A 是 M×N 矩阵,其中 M 是不等式的数目,而 N 是变量的数目(x0 中的元素数)。对于大型问题,如果使用支持稀疏数据的算法,则可将 A 作为稀疏矩阵传递。请参阅稀疏性在优化算法中的应用。
A 以如下形式编写 M 个线性不等式
A*x <= b,
其中,x 是由 N 个变量组成的列向量 x(:),b 是具有 M 个元素的列向量。
例如,假设有以下不等式:
x1 +2x2 ≤10
3x1 +4x2 ≤20
5x1 +6x2 ≤30,
通过输入以下约束来指定不等式。
A = [1,2;3,4;5,6]; b = [10;20;30];
示例: 要指定 x 分量总和等于或小于 1,请使用 A = ones(1,N) 和 b = 1。
数据类型: single | double
线性不等式约束,指定为实数向量。b 是与 A 矩阵相关的包含 M 个元素的向量。如果将 b 作为行向量传递,求解器会在内部将 b 转换为列向量 b(:)。
b 以如下形式编写 M 个线性不等式
A*x <= b,
其中,x 是由 N 个变量组成的列向量 x(:),A 是大小为 M×N 的矩阵。
例如,假设有以下不等式:
x1 + 2x2 ≤ 10
3x1 + 4x2 ≤ 20
5x1 + 6x2 ≤ 30。
通过输入以下约束来指定不等式。
A = [1,2;3,4;5,6]; b = [10;20;30];
示例: 要指定 x 分量总和等于或小于 1,请使用 A = ones(1,N) 和 b = 1。
数据类型: single | double
线性等式约束,指定为实矩阵。Aeq 是 Me×N 矩阵,其中 Me 是等式的数目,而 N 是变量的数目(x0 中的元素数)。对于大型问题,如果使用支持稀疏数据的算法,则可将 A 作为稀疏矩阵传递。请参阅稀疏性在优化算法中的应用。
Aeq 以如下形式编写 Me 个线性等式
Aeq*x = beq,
其中,x 是由 N 个变量组成的列向量 x(:),beq 是具有 Me 个元素的列向量。
例如,假设有以下不等式:
x1 +2x2 +3x3 =10
2x1 +4x2 + x3 =20,
通过输入以下约束来指定不等式。
Aeq = [1,2,3;2,4,1]; beq = [10;20];
示例: 要指定 x 分量总和为 1,请使用 Aeq = ones(1,N) 和 beq = 1。
数据类型: single | double
线性等式约束,指定为实数向量。beq 是与 Aeq 矩阵相关的包含 Me 个元素的向量。如果将 beq 作为行向量传递,求解器会在内部将 beq 转换为列向量 beq(:)。
beq 以如下形式编写 Me 个线性等式
Aeq*x = beq,
其中,x 是由 N 个变量组成的列向量 x(:),Aeq 是大小为 Me×N 的矩阵。
例如,请参考以下等式:
x1 + 2x2 + 3x3 = 10
2x1 + 4x2 + x3 = 20。
通过输入以下约束来指定等式。
Aeq = [1,2,3;2,4,1]; beq = [10;20];
示例: 要指定 x 分量总和为 1,请使用 Aeq = ones(1,N) 和 beq = 1。
数据类型: single | double
下界,指定为实数向量或实数数组。如果 x0 中的元素数等于 lb 中的元素数,则 lb 指定
x(i) >= lb(i)(对于全部 i)。
如果 numel(lb) < numel(x0),则 lb 指定
x(i) >= lb(i) (1 <= i <= numel(lb))。
如果 lb 的元素数少于 x0,求解器将发出警告。
示例: 要指定所有 x 分量为正,请使用 lb = zeros(size(x0))。
数据类型: single | double
上界,指定为实数向量或实数数组。如果 x0 中的元素数等于 ub 中的元素数,则 ub 指定
x(i) <= ub(i)(对于全部 i)。
如果 numel(ub) < numel(x0),则 ub 指定
x(i) <= ub(i) (1 <= i <= numel(ub))。
如果 ub 的元素数少于 x0,求解器将发出警告。
示例: 要指定 x 的所有分量小于 1,请使用 ub = ones(size(x0))。
数据类型: single | double
非线性约束,指定为函数句柄或函数名称。nonlcon 函数接受向量或数组 x,并返回两个数组 c(x) 和 ceq(x)。
c(x)是由x处的非线性不等式约束组成的数组。fmincon尝试满足对于
c的所有项,有c(x) <= 0。ceq(x)是由x处的非线性等式约束组成的数组。fmincon尝试满足对于
ceq的所有项,有ceq(x) = 0。
例如,
x = fmincon(@myfun,x0,A,b,Aeq,beq,lb,ub,@mycon)
其中 mycon 是一个 MATLAB 函数,例如
function [c,ceq] = mycon(x) c = ... % Compute nonlinear inequalities at x. ceq = ... % Compute nonlinear equalities at x.
SpecifyConstraintGradient 选项是 true,设置如下:options = optimoptions('fmincon',SpecifyConstraintGradient=true)nonlcon 还必须在第三个输出参量 GC 中返回 c(x) 的梯度,在第四个输出参量 GCeq 中返回 ceq(x) 的梯度。GC 和 GCeq 可以是稀疏的或稠密的。如果 GC 或 GCeq 较大,非零项相对较少,则通过将它们表示为稀疏矩阵,可以节省 interior-point 算法的运行时间和内存使用量。有关详细信息,请参阅非线性约束。注意
仅当 SpecifyObjectiveGradient 设置为 true 时,将 SpecifyConstraintGradient 设置为 true 才有效。在内部,目标折叠到约束中,因此求解器需要按顺序提供的两个梯度(目标和约束)以避免估计梯度。
注意
由于 Optimization Toolbox™ 函数只接受 double 类型的输入,用户提供的目标和非线性约束函数必须返回 double 类型的输出。
数据类型: char | function_handle | string
优化选项,指定为 optimoptions 的输出或 optimset 等返回的结构体。
一些选项适用于所有算法,其他选项则与特定算法相关。有关详细信息,请参阅优化选项参考。
optimoptions 显示中缺少某些选项。这些选项在下表中以斜体显示。有关详细信息,请参阅查看优化选项。
| 所有算法 | |||||
Algorithm | 选择优化算法:
有关选择算法的信息,请参阅选择算法。
如果您选择
| ||||
| CheckGradients | 将用户提供的导数(目标或约束的梯度)与有限差分导数进行比较。选项是 对于 以后的版本中将会删除 | ||||
ConstraintTolerance | 约束违反值的容差,非负标量。默认值为 对于 | ||||
| Diagnostics | 显示关于要最小化或求解的函数的诊断信息。选项是 | ||||
| DiffMaxChange | 有限差分梯度变量的最大变化(正标量)。默认值为 | ||||
| DiffMinChange | 有限差分梯度变量的最小变化(正标量)。默认值为 | ||||
Display | 显示级别(请参阅迭代输出):
| ||||
FiniteDifferenceStepSize | 有限差分的标量或向量步长因子。当您将
sign′(x) = sign(x)(例外是 sign′(0) = 1)。中心有限差分是
FiniteDifferenceStepSize 扩展为向量。对于正向有限差分,默认值为 sqrt(eps);对于中心有限差分,默认值为 eps^(1/3)。 对于 | ||||
FiniteDifferenceType | 用于估计梯度的有限差分,可以是 当同时估计这两种类型的有限差分时, 对于 | ||||
| FunValCheck | 检查目标函数值是否有效。默认设置 | ||||
MaxFunctionEvaluations | 允许的最大函数计算次数,非负整数。除 对于 | ||||
MaxIterations | 允许的最大迭代次数,非负整数。除 对于 | ||||
OptimalityTolerance | 一阶最优性的终止容差(非负标量)。默认值为 对于 | ||||
OutputFcn | 指定优化函数在每次迭代中调用的一个或多个用户定义的函数。传递函数句柄或函数句柄的元胞数组。默认值是“无”( | ||||
PlotFcn | 对算法执行过程中的各种进度测量值绘图,可以选择预定义的绘图,也可以自行编写绘图函数。传递内置绘图函数名称、函数句柄或由内置绘图函数名称或函数句柄组成的元胞数组。对于自定义绘图函数,传递函数句柄。默认值为“无”(
自定义绘图函数使用与输出函数相同的语法。请参阅Optimization Toolbox 的输出函数和输出函数和绘图函数语法。 对于 | ||||
SpecifyConstraintGradient | 用户定义的非线性约束函数梯度。当设置为默认值 对于 | ||||
SpecifyObjectiveGradient | 用户定义的目标函数梯度。请参阅 对于 | ||||
StepTolerance |
对于 | ||||
TypicalX | 典型的
| ||||
UseParallel | 此选项为 | ||||
| 信赖域反射算法 | |||||
FunctionTolerance | 函数值的终止容差,非负标量。默认值为 对于 | ||||
HessianFcn | 如果为 对于 | ||||
HessianMultiplyFcn | 黑塞矩阵乘法函数,指定为函数句柄。对于大规模结构问题,此函数计算黑塞矩阵乘积 W = hmfun(Hinfo,Y) 其中 上述第一个参量与目标函数 [f,g,Hinfo] = fun(x)
注意 要使用 请参阅黑塞矩阵乘法函数。有关示例,请参阅使用密集结构 Hessian 和线性等式进行最小化。 对于 | ||||
| HessPattern | 用于有限差分的黑塞矩阵稀疏模式。如果存在 ∂2 如果不方便在 当结构未知时,不要设置 | ||||
| MaxPCGIter | 预条件共轭梯度 (PCG) 迭代的最大次数,正标量。对于边界约束问题,默认值为 | ||||
| PrecondBandWidth | PCG 的预条件子上带宽,非负整数。默认情况下,使用对角预条件(上带宽为 0)。对于某些问题,增加带宽会减少 PCG 迭代次数。将 | ||||
SubproblemAlgorithm | 确定迭代步的计算方式。与 对于 | ||||
| TolPCG | PCG 迭代的终止容差,正标量。默认值为 | ||||
| 活动集算法 | |||||
FunctionTolerance | 函数值的终止容差,非负标量。默认值为 对于 | ||||
| MaxSQPIter | 允许的 SQP 迭代最大次数,正整数。默认值为 | ||||
| RelLineSrchBnd | 线搜索步长的相对边界(非负实数标量值)。x 中的总位移满足 |Δx(i)| ≤ relLineSrchBnd· max(|x(i)|,|typicalx(i)|)。当认为求解器采取的步过大时,可使用此选项控制 x 中位移的模。默认值为无边界 ( | ||||
| RelLineSrchBndDuration |
| ||||
| TolConSQP | 内部迭代 SQP 约束违反值的终止容差,正标量。默认值为 | ||||
| 内点算法 | |||||
BarrierParamUpdate | 指定
此选项会影响求解器的速度和收敛,但效果不容易预测。 | ||||
EnableFeasibilityMode | 当为 当 | ||||
HessianApproximation | 指定
注意 要使用 对于 | ||||
HessianFcn | 如果为 对于 | ||||
HessianMultiplyFcn | 用户提供的函数,它给出黑塞矩阵乘以向量的乘积(请参阅黑塞矩阵乘法函数)。传递函数句柄。 注意 要使用 对于 | ||||
HonorBounds | 默认值 对于 | ||||
| InitBarrierParam | 初始障碍值,正标量。有时尝试高于默认值 | ||||
| InitTrustRegionRadius | 信赖域的初始半径,正标量。对于未正确缩放的问题,选择小于默认值 的值可能会有所帮助,其中 n 是变量的数目。 | ||||
| MaxProjCGIter | 投影共轭梯度迭代次数的容差(停止条件);这是内部迭代,而不是算法的迭代次数。它是一个正整数,默认值为 | ||||
ObjectiveLimit | 容差(停止条件),标量。如果目标函数值低于 | ||||
ScaleProblem |
对于 | ||||
SubproblemAlgorithm | 确定迭代步的计算方式。默认值 对于 | ||||
| TolProjCG | 投影共轭梯度算法的相对容差(停止条件);它针对内部迭代,而不是算法迭代。它是一个正标量,默认值为 | ||||
| TolProjCGAbs | 投影共轭梯度算法的绝对容差(停止条件);它针对内部迭代,而不是算法迭代。它是一个正标量,默认值为 | ||||
| SQP 和 SQP 传统算法 | |||||
ObjectiveLimit | 容差(停止条件),标量。如果目标函数值低于 | ||||
ScaleProblem |
对于 | ||||
UseCodegenSolver | 对使用目标硬件上运行的软件版本的指示,指定为 | ||||
| 单精度代码生成 | |||||
Algorithm | 必须为 | ||||
ConstraintTolerance | 约束违反值的容差,非负标量。默认值为 | ||||
FiniteDifferenceStepSize | 有限差分的标量或向量步长因子。当您将
sign′(x) = sign(x)(例外是 sign′(0) = 1)。中心有限差分是
FiniteDifferenceStepSize 扩展为向量。对于正向有限差分,默认值为 sqrt(eps('single'));对于中心有限差分,默认值为 eps('single')^(1/3)。 | ||||
FiniteDifferenceType | 用于估计梯度的有限差分,可以是 当同时估计这两种类型的有限差分时, | ||||
MaxFunctionEvaluations | 允许的最大函数计算次数,非负整数。默认值为 | ||||
MaxIterations | |||||
ObjectiveLimit | 容差(停止条件),标量。如果目标函数值低于 | ||||
OptimalityTolerance | 一阶最优性的终止容差(非负标量)。默认值为 | ||||
ScaleProblem |
| ||||
SpecifyConstraintGradient | 用户定义的非线性约束函数梯度。当设置为默认值 | ||||
SpecifyObjectiveGradient | 用户定义的目标函数梯度。请参阅 | ||||
StepTolerance |
| ||||
TypicalX | 典型的 | ||||
UseCodegenSolver | 对使用目标硬件上运行的软件版本的指示,指定为 | ||||
示例: options = optimoptions('fmincon','SpecifyObjectiveGradient',true,'SpecifyConstraintGradient',true)
问题结构体,指定为含有以下字段的结构体:
| 字段名称 | 条目 |
|---|---|
| 目标函数 |
| x 的初始点 |
| 线性不等式约束的矩阵 |
| 线性不等式约束的向量 |
| 线性等式约束的矩阵 |
| 线性等式约束的向量 |
lb | 由下界组成的向量 |
ub | 由上界组成的向量 |
| 非线性约束函数 |
| 'fmincon' |
| 用 optimoptions 创建的选项 |
您必须在 problem 结构体中至少提供 objective、x0、solver 和 options 字段。
数据类型: struct
输出参量
解处的目标函数值,以实数形式返回。通常,fval = fun(x)。
fmincon 停止的原因,以整数形式返回。
所有算法: | |
| 一阶最优性测度小于 |
| 迭代次数超出 |
| 由输出函数或绘图函数停止。 |
| 找不到可行点。 |
除 | |
|
|
仅 | |
| 目标函数值的变化小于 |
仅 | |
| 搜索方向的模小于 2* |
| 搜索方向中方向导数的模小于 2* |
| |
| 当前迭代的目标函数低于 |
有关优化过程的信息,以包含下列字段的结构体形式返回:
iterations | 执行的迭代次数 |
funcCount | 函数计算次数 |
lssteplength | 相对于搜索方向的线搜索步的大小(仅适用于 |
constrviolation | 约束函数的最大值 |
stepsize |
|
algorithm | 使用的优化算法 |
cgiterations | PCG 迭代总次数(适用于 |
firstorderopt | 一阶最优性的测度 |
bestfeasible | 迭代结束时遇到的最佳(最低目标函数)可行点。具有以下字段的结构体:
如果找不到可行点,则 |
message | 退出消息 |
解处的梯度,以实数向量形式返回。grad 给出 fun 在 x(:) 点处的梯度。
逼近黑塞矩阵,以实矩阵形式返回。有关 hessian 的含义,请参阅黑塞矩阵输出。
限制
fmincon是基于梯度的方法,旨在处理目标函数和约束函数均为连续且具有连续一阶导数的问题。对于
'trust-region-reflective'算法,您必须在fun中提供梯度,并将'SpecifyObjectiveGradient'选项设置为true。'trust-region-reflective'算法不允许相等的上界和下界。例如,如果lb(2)==ub(2),则fmincon给出以下错误:Equal upper and lower bounds not permitted in trust-region-reflective algorithm. Use either interior-point or SQP algorithms instead.
传递黑塞矩阵有两种不同的语法,传递
HessianMultiplyFcn函数也有两种不同的语法;一种针对trust-region-reflective,另一种针对interior-point。请参阅包含黑塞函数。对于
trust-region-reflective,拉格朗日函数的黑塞矩阵与目标函数的黑塞矩阵相同。您将黑塞矩阵作为目标函数的第三个输出进行传递。对于
interior-point,拉格朗日函数的黑塞矩阵涉及拉格朗日乘数和非线性约束函数的黑塞矩阵。您将黑塞函数作为单独的函数传递,该函数同时考虑当前点x和拉格朗日乘数结构体lambda。
当问题不可行时,
fmincon会尝试将最大约束值最小化。
详细信息
fmincon 将黑塞矩阵作为可选输入。此黑塞矩阵是拉格朗日函数二阶导数的矩阵(请参阅公式 1),即,
| (3) |
有关如何向 trust-region-reflective 或 interior-point 算法提供黑塞矩阵的详细信息,请参阅包含黑塞函数。
active-set 和 sqp 算法不接受 黑塞 矩阵作为输入。它们计算拉格朗日函数的黑塞矩阵的拟牛顿逼近。
interior-point 算法提供多种 'HessianApproximation' 选项;请参阅为内点 fmincon 选择输入黑塞函数逼近方法:
'bfgs'-fmincon通过稠密矩阵拟牛顿逼近来计算黑塞矩阵。这是默认黑塞逼近。'lbfgs'-fmincon通过限制内存使用量的大规模拟牛顿逼近计算黑塞矩阵。此选项使用默认内存量,即进行 10 次迭代。{'lbfgs',positive integer}-fmincon通过限制内存使用量的大规模拟牛顿逼近计算黑塞矩阵。正整数指定要保留记录的最近迭代次数。'finite-difference'-fmincon通过梯度的有限差分计算黑塞矩阵乘以向量的乘积。您必须提供目标函数的梯度,还要提供非线性约束的梯度(如果存在)。将'SpecifyObjectiveGradient'选项设置为true,并在适用时将'SpecifyConstraintGradient'选项设置为true。您必须将'SubproblemAlgorithm'设置为'cg'。
interior-point 和 trust-region-reflective 算法允许您提供黑塞矩阵乘法函数。此函数给出黑塞函数乘以向量的乘积结果,而不直接计算黑塞函数。这可以节省内存。有关详细信息,请参阅黑塞矩阵乘法函数。
接下来的几项列出了可能增强的退出消息 fmincon。增强的退出消息在消息的第一句中给出了详细信息的链接。
求解器找到一个点,它似乎是局部最小值,因为该点是可行的(约束 ConstraintTolerance容差)和一阶最优性测度小于OptimalityTolerance宽容。
有关如何继续的建议,请参阅求解成功后。
最初的要点似乎是局部最小值,因为该点是可行的(约束 ConstraintTolerance容差),以及一阶最优性测度小于OptimalityTolerance宽容。
有关如何继续的建议,请参阅终点等于初始点。
求解器可能已经达到了 局部最小值,但不能确定,因为 一阶最优性测度 不小于 OptimalityTolerance容差。约束满足ConstraintTolerance约束约束。
有关如何继续的建议,请参阅可能是局部最小值。
fmincon 收敛到不满足所有约束的点,在约束范围内 容差 称为ConstraintTolerance。fmincon 停止的原因是上一个步长太小。当相对步长低于 StepTolerance 容忍度,则迭代结束。
有关如何继续的建议,请参阅收敛于不可行点。
求解器停止,因为它在将目标函数最小化至要求的容差之前达到了迭代或函数计算次数的限制。
有关如何继续的建议,请参阅迭代或函数计算次数太多。
接下来的几项包含以下术语的定义 fmincon 退出消息。
函数的局部最小值是指这样的一个点:其函数值小于附近的点,但可能大于远处的点。
全局最小值是函数值小于所有其他可行点的点。
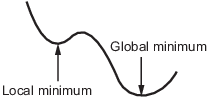
求解器尝试找到局部最小值。该结果也可能是全局最小值。有关详细信息,请参阅局部最优与全局最优。
一般来说,容差是一个阈值,超过阈值时将终止求解器的迭代。有关容差的详细信息,请参阅容差和停止条件。
约束 容差 称为 ConstraintTolerance,是当前点所有约束函数值的最大值。
ConstraintTolerance 的运算原理不同于其他容差。如果不满足 ConstraintTolerance(即,如果约束函数的模超过 ConstraintTolerance),求解器将尝试继续求解,除非因其他原因而停止。求解器不会仅仅因为满足 ConstraintTolerance 就停止。
约束违反值是当前点所有约束函数值的最大值。这是根据名为 ConstraintTolerance 的 容差 衡量的。
ConstraintTolerance 的运算原理不同于其他容差。如果不满足 ConstraintTolerance(即,如果约束函数的模超过 ConstraintTolerance),求解器将尝试继续求解,除非因其他原因而停止。求解器不会仅仅因为满足 ConstraintTolerance 就停止。
可行方向是从当前点开始的局部满足约束的向量。它们或者指向满足约束的区域内部,或者与绑定约束的边界相切。
约束问题的一阶最优性测度是以下两个量的最大值:
对于无约束问题,它是梯度向量分量绝对值的最大值(也称为无穷范数)。
在最小化点处,此值应为零。
有关详细信息,包括这些方程中所有变量的定义,请参阅一阶最优性测度。
称为 OptimalityTolerance 的容差与一阶最优性测度相关。当一阶最优性测度小于 OptimalityTolerance 时,迭代结束。有关详细信息,请参阅一阶最优性测度。
目标函数的预测变化是求解器估计在当前点沿估计的最佳搜索方向移动时目标函数将减少的量。此估计的减少量是目标在当前点的梯度与搜索方向的内积乘以步长。Optimization Toolbox 求解器通过各种算法计算搜索方向,如约束非线性优化算法中所述。
求解器的每次迭代都会对输出函数(或绘图函数)进行一次计算。它可以在求解器的运行过程中报告许多优化量,并可以停止求解器的运行。
有关详细信息,请参阅Optimization Toolbox 的输出函数或绘图函数。
MaxSQPIter 是容差求解器执行的序列二次规划子问题迭代次数。当求解器对子问题进行了 MaxSQPIter 次迭代后,子问题迭代结束。
有关详细信息,请参阅序列二次规划 (SQP)。
x 的所有元素的相对变化是归一化的步长向量。运行此向量通过用目标函数计算位置的变化除以当前位置的无穷范数得到。如果这个相对范数的最大值低于 StepTolerance容差,则迭代结束。
当前步长是计算目标函数时所在位置的变化的范数。在这种情况下,fmincon 使用相对大小:步长除以当前位置的无穷范数。当这个相对步长低于 StepTolerance容差,则迭代结束。
StepTolerance 是一个 容差 表示最后一步的大小,即评估目标函数的位置变化的大小。
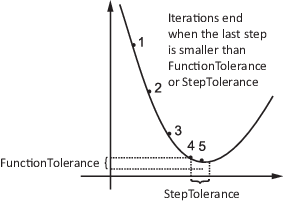
约束违反值是当前点未满足的约束函数。这些函数的梯度范数太小,求解器无法继续。当前点不可行(某些约束违反超出了 ConstraintTolerance容差)。
有关如何继续的建议,请参阅收敛于不可行点。
搜索方向是从当前点开始的向量,求解器沿该向量寻找改进。此方向的范数是无穷范数,即搜索向量的分量绝对值的最大值。
Optimization Toolbox 求解器通过各种算法计算搜索方向,如约束非线性优化算法中所述。
fmincon 通过采用有限差分来估计目标函数和非线性约束函数的梯度。有限差分计算在函数明确定义的区域之外进行,返回 Inf、NaN 或复数结果。
有关求解器如何计算和使用梯度的详细信息,请参阅约束非线性优化算法。有关如何继续的建议,请参阅6.提供梯度或雅可比矩阵。
fmincon "interior-point" 算法可以使用专用算法来搜索可行点。通过使用 optimoptions 将 EnableFeasibilityMode 选项设置为 true 来启用此搜索。要提高处理难题的效率,请将 SubproblemAlgorithm 选项设置为 "cg":
options = optimoptions("fmincon",... Algorithm="interior-point",... EnableFeasibilityMode=true,... SubproblemAlgorithm="cg");
有关 EnableFeasibilityMode 算法的详细信息,请参阅可行性模式。
算法
有关选择算法的帮助,请参阅fmincon 算法。要设置算法,请使用 optimoptions 创建 options,并使用 'Algorithm' 名称-值对组。
本节在后续部分提供每种算法的简要总结或信息指南。
fmincon 内点算法中说明了此算法。在 [1]、[41] 和 [9] 中有更广泛的说明。
fmincon 'sqp' 和 'sqp-legacy' 算法类似于活动集优化中所述的 'active-set' 算法。fmincon SQP 算法说明了主要区别。这些区别总结如下:
'trust-region-reflective' 算法是一种子空间信赖域方法,基于 [3] 和 [4] 中所述的内部反射牛顿法。每次迭代都涉及使用预条件共轭梯度法 (PCG) 来近似求解大型线性系统。请参阅fmincon 信赖域反射算法中有关信赖域和预条件共轭梯度法的说明。
替代功能
App
优化实时编辑器任务为 fmincon 提供了一个可视化界面。
参考
[1] Byrd, R. H., J. C. Gilbert, and J. Nocedal. “A Trust Region Method Based on Interior Point Techniques for Nonlinear Programming.” Mathematical Programming, Vol 89, No. 1, 2000, pp. 149–185.
[2] Byrd, R. H., Mary E. Hribar, and Jorge Nocedal. “An Interior Point Algorithm for Large-Scale Nonlinear Programming.” SIAM Journal on Optimization, Vol 9, No. 4, 1999, pp. 877–900.
[3] Coleman, T. F. and Y. Li. “An Interior, Trust Region Approach for Nonlinear Minimization Subject to Bounds.” SIAM Journal on Optimization, Vol. 6, 1996, pp. 418–445.
[4] Coleman, T. F. and Y. Li. “On the Convergence of Reflective Newton Methods for Large-Scale Nonlinear Minimization Subject to Bounds.” Mathematical Programming, Vol. 67, Number 2, 1994, pp. 189–224.
[5] Gill, P. E., W. Murray, and M. H. Wright. Practical Optimization, London, Academic Press, 1981.
[6] Han, S. P. “A Globally Convergent Method for Nonlinear Programming.” Journal of Optimization Theory and Applications, Vol. 22, 1977, pp. 297.
[7] Powell, M. J. D. “A Fast Algorithm for Nonlinearly Constrained Optimization Calculations.” Numerical Analysis, ed. G. A. Watson, Lecture Notes in Mathematics, Springer-Verlag, Vol. 630, 1978.
[8] Powell, M. J. D. “The Convergence of Variable Metric Methods For Nonlinearly Constrained Optimization Calculations.” Nonlinear Programming 3 (O. L. Mangasarian, R. R. Meyer, and S. M. Robinson, eds.), Academic Press, 1978.
[9] Waltz, R. A., J. L. Morales, J. Nocedal, and D. Orban. “An interior algorithm for nonlinear optimization that combines line search and trust region steps.” Mathematical Programming, Vol 107, No. 3, 2006, pp. 391–408.
扩展功能
用法说明和限制:
fmincon支持使用codegen(MATLAB Coder) 函数或 MATLAB Coder™ 生成代码。您必须拥有 MATLAB Coder 许可证才能生成代码。目标硬件必须支持标准双精度浮点计算或标准单精度浮点计算。
代码生成目标与 MATLAB 求解器不使用相同的数学核心函数库。因此,代码生成解可能不同于求解器解,尤其是对于病态问题。
要在生成代码前在 MATLAB 中测试代码,请将
UseCodegenSolver选项设置为true。这样,求解器便可使用代码生成创建的相同代码。生成的所有代码必须为 MATLAB 代码。特别是,您不能将自定义黑盒函数用作
fmincon的目标函数。您可以使用coder.ceval计算用 C 或 C++ 编码的自定义函数。但是,自定义函数必须在 MATLAB 函数中调用。在生成代码时,
fmincon不支持problem参量。[x,fval] = fmincon(problem) % Not supported您必须使用函数句柄(而不是字符串或字符名称)来指定目标函数和任何非线性约束函数。
x = fmincon(@fun,x0,A,b,Aeq,beq,lb,ub,@nonlcon) % Supported % Not supported: fmincon('fun',...) or fmincon("fun",...)
所有
fmincon输入矩阵(如A、Aeq、lb和ub)都必须是满矩阵,而不能是稀疏矩阵。您可以使用full函数将稀疏矩阵转换为满矩阵。lb和ub参量的条目数必须与x0参量相同,或必须为空[]。如果您的目标硬件不支持无限边界,请使用
optim.coder.infbound。对于涉及嵌入式处理器的高级代码优化,您还需要 Embedded Coder® 许可证。
您必须包括适用于
fmincon的选项,并使用optimoptions指定这些选项。选项中必须包括Algorithm并将其设置为'sqp'或'sqp-legacy'。options = optimoptions("fmincon",Algorithm="sqp"); [x,fval,exitflag] = fmincon(fun,x0,A,b,Aeq,beq,lb,ub,nonlcon,options);
代码生成支持以下选项:
Algorithm- 必须为'sqp'或'sqp-legacy'。ConstraintToleranceFiniteDifferenceStepSizeFiniteDifferenceTypeMaxFunctionEvaluationsMaxIterationsObjectiveLimitOptimalityToleranceScaleProblemSpecifyConstraintGradientSpecifyObjectiveGradientStepToleranceTypicalXUseCodegenSolver
生成的代码只会对选项进行有限的错误检查。更新选项的推荐方法是使用
optimoptions,而不是圆点表示法。opts = optimoptions('fmincon','Algorithm','sqp'); opts = optimoptions(opts,'MaxIterations',1e4); % Recommended opts.MaxIterations = 1e4; % Not recommended
不要从文件中加载选项。否则会导致代码生成失败。请在代码中创建选项。
通常,如果您指定了不受支持的选项,在代码生成过程中会以静默方式忽略该选项。但是,如果使用圆点表示法指定绘图函数或输出函数,代码生成可能引发错误。为确保可靠性,请仅指定支持的选项。
由于不支持输出函数和绘图函数,
fmincon不会返回退出标志 –1。为
fmincon生成的代码中返回的output结构体不包含bestfeasible字段。
有关示例,请参阅优化代码生成基础知识。
要并行运行,请将 'UseParallel' 选项设置为 true。
options = optimoptions('solvername','UseParallel',true)
有关详细信息,请参阅在 Optimization Toolbox 中使用并行计算。
版本历史记录
在 R2006a 之前推出将新的 UseCodegenSolver 选项设置为 true,以便 fmincon 使用与代码生成所创建软件相同的版本。通过此选项,可以在生成代码或将代码部署到硬件之前检查求解器的行为。对于支持单精度代码生成的求解器,生成的代码也可以支持单精度硬件。您可以在生成代码时包含该选项;该选项对代码生成没有影响,但保留该选项可以省去删除它的步骤。尽管生成的代码与 MATLAB 代码相同,但结果可能因链接的数学库不同而略有差异。
您可以在单精度浮点硬件上为 fmincon 生成代码。有关说明,请参阅单精度代码生成。
以后的版本中将会删除 CheckGradients 选项。要检查目标函数或非线性约束函数的一阶导数,请使用 checkGradients 函数。
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.
选择网站
选择网站以获取翻译的可用内容,以及查看当地活动和优惠。根据您的位置,我们建议您选择:。
您也可以从以下列表中选择网站:
如何获得最佳网站性能
选择中国网站(中文或英文)以获得最佳网站性能。其他 MathWorks 国家/地区网站并未针对您所在位置的访问进行优化。
美洲
- América Latina (Español)
- Canada (English)
- United States (English)
欧洲
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)