fminbnd

查找单变量函数在定区间上的局部最小值

全页折叠

语法

x = fminbnd(fun,x1,x2)

x = fminbnd(fun,x1,x2,options)

x = fminbnd(problem)

[x,fval] = fminbnd(___)

[x,fval,exitflag] = fminbnd(___)

[x,fval,exitflag,output] = fminbnd(___)

说明

fminbnd 是一个一维最小化求解器，用于求由以下条件指定的问题的局部最小值：

$\min_{x} f (x) such that x_{1} < x < x_{2} .$

x、x₁ 和 x₂ 是有限标量，f(x) 是返回标量的函数。

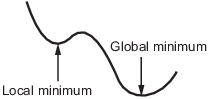
如果区间 (x1,x2) 上存在多个局部最小值，则 fminbnd 仅返回一个，这并不保证它是全局最小值。有关详细信息，请参阅局部最小值与全局最小值。

x = fminbnd(fun,x1,x2) 返回一个值 x，该值是 fun 中描述的标量值函数在区间 x1 < x < x2 中的局部最小值点。

示例

x = fminbnd(fun,x1,x2,options) 使用 options 中指定的优化选项执行最小化计算。使用 optimset 可设置这些选项。

示例

x = fminbnd(problem) 最小化 problem，其中 problem 是结构体。

对于任何输入参量，[x,fval] = fminbnd(___) 返回目标函数在 fun 的解 x 处计算出的值。

示例

[x,fval,exitflag] = fminbnd(___) 还返回描述退出条件的值 exitflag。

[x,fval,exitflag,output] = fminbnd(___) 还返回一个包含有关优化的信息的结构体 output。

示例

全部折叠

`sin` 的最小值

打开实时脚本

求 $\sin (x)$ 函数在 $0 < x < 2 π$ 范围内的最小值的点。

fun = @sin;
x1 = 0;
x2 = 2*pi;
x = fminbnd(fun,x1,x2)

x = 
4.7124

为了显示精度，此值与正确值 $x = 3 π / 2$ 相同。

3*pi/2

ans = 
4.7124

最小化由文件指定的函数

打开脚本

最小化由单独的函数文件指定的函数。函数接受输入点 x 并返回表示 x 处的目标函数值的实数标量。

将以下函数编写为文件，并将文件保存为您的 MATLAB® 路径中的 scalarobjective.m。

function f = scalarobjective(x)
f = 0;
for k = -10:10
    f = f + (k+1)^2*cos(k*x)*exp(-k^2/2);
end

求在区间 1 <= x <= 3 内最小化 scalarobjective 的 x。

x = fminbnd(@scalarobjective,1,3)

x =

    2.0061

具有额外参数时的最小化

打开实时脚本

存在额外参数时最小化函数。函数 $\sin (x - a)$ 有一个最小值，该值取决于参数 $a$ 的值。创建 $x$ 的匿名函数，其中包含参数 $a$ 的值。在区间 $0 < x < 2 π$ 内最小化此函数。

a = 9/7;
fun = @(x)sin(x-a);
x = fminbnd(fun,1,2*pi)

x = 
5.9981

此答案是正确的；理论值为

3*pi/2 + 9/7

ans = 
5.9981

有关包括额外参数的详细信息，请参阅参数化函数。

监视迭代

打开实时脚本

监视 fminbnd 在区间 $0 < x < 2 π$ 内最小化函数 $\sin (x)$ 时所采用的步骤。

fun = @sin;
x1 = 0;
x2 = 2*pi;
options = optimset('Display','iter');
x = fminbnd(fun,x1,x2,options)

 
 Func-count     x          f(x)         Procedure
    1        2.39996      0.67549        initial
    2        3.88322     -0.67549        golden
    3        4.79993    -0.996171        golden
    4        5.08984    -0.929607        parabolic
    5        4.70582    -0.999978        parabolic
    6         4.7118           -1        parabolic
    7        4.71239           -1        parabolic
    8        4.71236           -1        parabolic
    9        4.71242           -1        parabolic
 
Optimization terminated:
 the current x satisfies the termination criteria using OPTIONS.TolX of 1.000000e-04

x = 
4.7124

求最小值的位置和函数值

打开实时脚本

求 $\sin (x)$ 的最小值的位置以及在 $0 < x < 2 π$ 区间内的最小值。

fun = @sin;
[x,fval] = fminbnd(fun,1,2*pi)

x = 
4.7124

fval = 
-1.0000

获取所有信息

打开实时脚本

通过请求所有输出返回有关 fminbnd 求解过程的所有信息。此外，还使用绘图函数监视求解过程。

fun = @sin;
x1 = 0;
x2 = 2*pi;
options = optimset('PlotFcns',@optimplotfval);
[x,fval,exitflag,output] = fminbnd(fun,x1,x2,options)

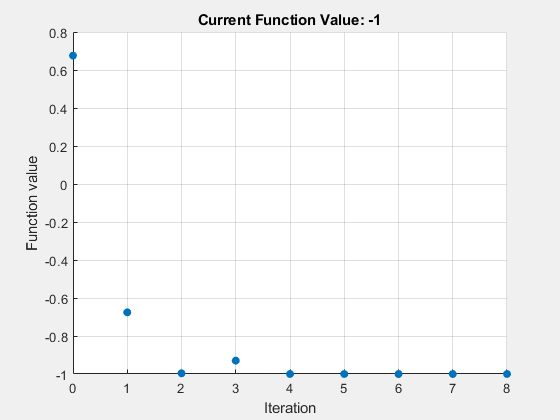
Figure Optimization Plot Function contains an axes object. The axes object with title Current Function Value: -1, xlabel Iteration, ylabel Function value contains an object of type scatter.

x = 
4.7124

fval = 
-1.0000

exitflag = 
1

output = struct with fields:
    iterations: 8
     funcCount: 9
     algorithm: 'golden section search, parabolic interpolation'
       message: 'Optimization terminated:↵ the current x satisfies the termination criteria using OPTIONS.TolX of 1.000000e-04 ↵'

输入参数

全部折叠

`fun` — 要最小化的函数
函数句柄 | 函数名称

要最小化的函数，指定为函数句柄或函数名称。fun 是一个接受实数标量 x 的函数，并返回实数标量 f（在 x 处计算的目标函数值）。

将 fun 指定为文件的函数句柄：

x = fminbnd(@myfun,x1,x2)

其中 myfun 是一个 MATLAB^® 函数，例如

function f = myfun(x)
f = ...            % Compute function value at x

您还可以为匿名函数指定 fun 作为函数句柄：

x = fminbnd(@(x)norm(x)^2,x1,x2);

示例: fun = @(x)-x*exp(-3*x)

数据类型: char | function_handle | string

`x1` — 下界
有限实数标量

下界，指定为有限实数标量。

示例: x1 = -3

数据类型: double

`x2` — 上界
有限实数标量

上界，指定为有限实数标量。

示例: x2 = 5

数据类型: double

`options` — 优化选项
结构体，例如 `optimset` 返回的结构体

优化选项，指定为结构体，例如 optimset 返回的结构体。您可以使用 optimset 设置或更改 options 结构体中这些字段的值。有关详细信息，请参阅设置优化选项。

`Display`	显示级别（请参阅优化求解器迭代输出）： `'notify'`（默认值）仅在函数未收敛时显示输出。 `'off'` 或 `'none'` 不显示输出。 `'iter'` 在每次迭代时显示输出。 `'final'` 仅显示最终输出。
`FunValCheck`	检查目标函数值是否有效。当目标函数返回的值为 `complex` 或 `NaN` 时，默认 `'off'` 允许 `fminbnd` 继续。当目标函数返回的值是 `complex` 或 `NaN` 时，`'on'` 设置会抛出错误。
`MaxFunEvals`	允许的函数求值的最大次数，为正整数。默认值为 `500`。请参阅容差和终止条件。
`MaxIter`	允许的迭代最大次数，为正整数。默认值为 `500`。请参阅容差和终止条件。
`OutputFcn`	以函数句柄或函数句柄的元胞数组的形式来指定优化函数在每次迭代时调用的一个或多个用户定义函数。默认值是“无”(`[]`)。请参阅优化求解器输出函数。
`PlotFcns`	绘制算法执行过程中的各个进度测量值。从预定义绘图中选择，或者自行编写。传递函数名称、函数句柄或者函数名称或句柄的元胞数组。默认值是“无”(`[]`)： `@optimplotx` 绘制当前点 `@optimplotfunccount` 绘制函数计数 `@optimplotfval` 绘制函数值有关编写自定义绘图函数的信息，请参阅优化求解器绘制函数。
`TolX`	关于正标量 `x` 的终止容差。默认值为 `1e-4`。请参阅容差和终止条件。

示例: options = optimset('Display','iter')

数据类型: struct

`problem` — 问题结构体
结构体

问题结构体，指定为含有以下字段的结构体。

字段名称	条目
`objective`	目标函数
`x1`	左端点
`x2`	右端点
`solver`	`'fminbnd'`
`options`	Options 结构体，例如 `optimset` 返回的结构体

数据类型: struct

输出参量

全部折叠

`x` — 解
实数标量

解，以实数标量形式返回。通常情况下，当 exitflag 为正时，x 是该问题的局部解。请参阅局部最小值与全局最小值。

`fval` — 解处的目标函数值
实数

解处的目标函数值，以实数形式返回。通常，fval = fun(x)。

`exitflag` — `fminbnd` 停止的原因
整数

fminbnd 停止的原因，以整数形式返回。

`1`	函数收敛于解 `x`。
`0`	迭代次数超出 `options.MaxIter` 或函数计算次数超过 `options.MaxFunEvals`。
`-1`	由输出函数或绘图函数停止。
`-2`	边界不一致，这意味着 `x1 > x2`。

`output` — 有关优化过程的信息
结构体

有关优化过程的信息，以包含下列字段的结构体形式返回：

`iterations`	执行的迭代次数
`funcCount`	函数计算次数
`algorithm`	`'golden section search, parabolic interpolation'`
`message`	退出消息

限制

要最小化的函数必须是连续的。
fminbnd 只能给出局部解。
当解在区间的边界上时，fminbnd 可能表现出慢收敛。

详细信息

全部折叠

局部最小值与全局最小值

通常，优化求解器返回一个局部最小值（或最优值）。结果可能是全局最小值（或最优值），但也可能不是。

函数的局部最小值是指这样的一个点：其函数值小于附近的点，但可能大于远处的点。
全局最小值是函数值小于所有其他可行点的点。

Curve with two dips; the lower dip is the global minimum, the higher dip is a local minimum

MATLAB 和 Optimization Toolbox™ 优化求解器通常返回局部最小值。Global Optimization Toolbox 求解器可以搜索全局最小值，但无法保证其解是全局解。有关全局搜索的示例，请参阅寻找全局或多个局部最小值 (Global Optimization Toolbox)。

算法

fminbnd 是一个函数文件。算法基于黄金分割搜索和抛物线插值方法。除非左端点 x₁ 非常靠近右端点 x₂，否则 fminbnd 从不计算 fun 在端点处的值，因此只需要为 x 在区间 x₁ < x < x₂ 中定义 fun。

如果最小值实际上出现在 x₁ 或 x₂ 处，则 fminbnd 返回区间 (x₁,x₂) 内部靠近最小值的点 x。在本例中，x 与最小值点的距离不超过 2*(TolX + 3*abs(x)*sqrt(eps))。有关算法的详细信息，请参阅 [1] 或 [2]。

替代功能

App

优化实时编辑器任务为 fminbnd 提供可视化界面。

参考

[1] Forsythe, G. E., M. A. Malcolm, and C. B. Moler. Computer Methods for Mathematical Computations. Englewood Cliffs, NJ: Prentice Hall, 1976.

[2] Brent, Richard. P. Algorithms for Minimization without Derivatives. Englewood Cliffs, NJ: Prentice-Hall, 1973.

扩展功能

全部展开

C/C++ 代码生成
使用 MATLAB® Coder™ 生成 C 代码和 C++ 代码。

对于 C/C++ 代码生成：

fminbnd 不支持问题结构体参量。
fminbnd 会忽略 Display 选项，且不显示迭代输出或退出消息。要检查解的质量，请检查退出标志。
输出结构体不包含 algorithm 或 message 字段。
fminbnd 忽略 OutputFcn 和 PlotFcns 选项。

基于线程的环境
使用 MATLAB® `backgroundPool` 在后台运行代码或使用 Parallel Computing Toolbox™ `ThreadPool` 加快代码运行速度。

此函数完全支持基于线程的环境。有关详细信息，请参阅在基于线程的环境中运行 MATLAB 函数。

版本历史记录

在 R2006a 之前推出

另请参阅

fminsearch | fzero | optimset | 优化

fminbnd

语法

说明

示例

sin 的最小值

最小化由文件指定的函数

具有额外参数时的最小化

监视迭代

求最小值的位置和函数值

获取所有信息

输入参数

fun — 要最小化的函数 函数句柄 | 函数名称

x1 — 下界 有限实数标量

x2 — 上界 有限实数标量

options — 优化选项 结构体，例如 optimset 返回的结构体

problem — 问题结构体 结构体

输出参量

x — 解 实数标量

fval — 解处的目标函数值 实数

exitflag — fminbnd 停止的原因 整数

output — 有关优化过程的信息 结构体

限制

详细信息

局部最小值与全局最小值

算法

替代功能

App

参考

扩展功能

C/C++ 代码生成 使用 MATLAB® Coder™ 生成 C 代码和 C++ 代码。

基于线程的环境 使用 MATLAB® backgroundPool 在后台运行代码或使用 Parallel Computing Toolbox™ ThreadPool 加快代码运行速度。

版本历史记录

另请参阅

主题

`sin` 的最小值

`fun` — 要最小化的函数
函数句柄 | 函数名称

`x1` — 下界
有限实数标量

`x2` — 上界
有限实数标量

`options` — 优化选项
结构体，例如 `optimset` 返回的结构体

`problem` — 问题结构体
结构体

`x` — 解
实数标量

`fval` — 解处的目标函数值
实数

`exitflag` — `fminbnd` 停止的原因
整数

`output` — 有关优化过程的信息
结构体

C/C++ 代码生成
使用 MATLAB® Coder™ 生成 C 代码和 C++ 代码。

基于线程的环境
使用 MATLAB® `backgroundPool` 在后台运行代码或使用 Parallel Computing Toolbox™ `ThreadPool` 加快代码运行速度。