优化非线性函数

求一元函数的最小值

如果给定了一个一元数学函数，可以使用 fminbnd 函数求该函数在给定区间中的局部最小值。例如，请考虑 MATLAB® 提供的 humps.m 函数。下图显示了 humps 的图。

x = -1:.01:2;
y = humps(x);
plot(x,y)
xlabel('x')
ylabel('humps(x)')
grid on

Figure contains an axes object. The axes object contains an object of type line.

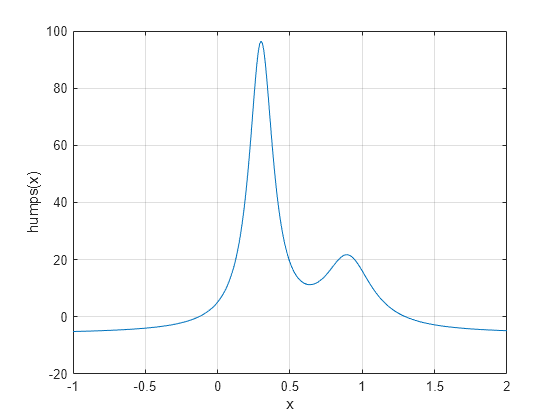
若要计算 humps 函数在 (0.3,1) 范围内的最小值，请使用

x = fminbnd(@humps,0.3,1)

x = 0.6370

您可以通过使用 optimset 创建选项并将 Display 选项设置为 'iter' 来查看求解过程的详细信息。将所得选项传递给 fminbnd。

options = optimset('Display','iter');
x = fminbnd(@humps,0.3,1,options)

 
 Func-count     x          f(x)         Procedure
    1       0.567376      12.9098        initial
    2       0.732624      13.7746        golden
    3       0.465248      25.1714        golden
    4       0.644416      11.2693        parabolic
    5         0.6413      11.2583        parabolic
    6       0.637618      11.2529        parabolic
    7       0.636985      11.2528        parabolic
    8       0.637019      11.2528        parabolic
    9       0.637052      11.2528        parabolic
 
Optimization terminated:
 the current x satisfies the termination criteria using OPTIONS.TolX of 1.000000e-04

x = 0.6370

这种迭代输出显示了 x 的当前值以及每次计算函数时 f(x) 处的函数值。对于 fminbnd，一次函数计算对应一次算法迭代。最后一列显示 fminbnd 在每次迭代中使用的过程，即黄金分割搜索或抛物线插值。有关详细信息，请参阅优化求解器迭代输出。

求多元函数的最小值

fminsearch 函数与 fminbnd 类似，不同之处在于前者处理多变量函数。请指定起始向量 x₀，而非起始区间。fminsearch 尝试返回一个向量 x，该向量是数学函数在此起始向量附近的局部最小值。

要尝试执行 fminsearch，请创建一个三元（即 x、y 和 z）函数 three_var。

function b = three_var(v)
x = v(1);
y = v(2);
z = v(3);
b = x.^2 + 2.5*sin(y) - z^2*x^2*y^2;

现在，使用 x = -0.6、y = -1.2 和 z = 0.135 作为起始值求此函数的最小值。

v = [-0.6,-1.2,0.135];
a = fminsearch(@three_var,v)

a =
    0.0000   -1.5708    0.1803

求函数最大值

fminbnd 和 fminsearch 求解器尝试求目标函数的最小值。如果您有最大化问题，即以下形式的问题：

$\max_{x} f (x),$

然后定义 g(x) = –f(x)，并对 g 取最小值。

例如，要计算 tan(cos(x)) 在 x = 5 附近的最大值，请计算：

[x fval] = fminbnd(@(x)-tan(cos(x)),3,8)

x =
    6.2832

fval =
   -1.5574

最大值为 1.5574（报告的 fval 的负值），并出现在 x = 6.2832。此答案是正确的，因为最大值为 tan(1) = 1.5574（最多五位数），该值出现在 x = 2π = 6.2832 位置。

`fminsearch` 算法

fminsearch 使用 Lagarias 等人的著作 [1] 中所述的 Nelder-Mead 单纯形算法。此算法对 n 维向量 x 使用 n + 1 个点组成的单纯形。此算法首先向 x₀ 添加各分量 x₀(i) 的 5%，以围绕初始估计值 x₀ 生成一个单纯形。然后，该算法使用上述 n 个向量作为单纯形的除 x₀ 之外的元素。（如果 x₀(i) = 0，则算法使用 0.00025 作为分量 i）。然后，此算法按照以下过程反复修改单纯形。

注意

fminsearch 迭代输出方式中的关键字在相应的步骤说明后以粗体形式显示。

用 x(i) 表示当前单纯形中的点列表 i = 1,...,n + 1。
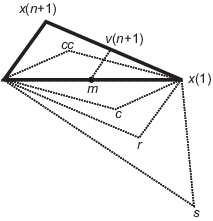
按最小函数值 f(x(1)) 到最大函数值 f(x(n + 1)) 的顺序对单纯形中的点进行排序。在迭代的每个步骤中，此算法都会放弃当前的最差点 x(n + 1) 并接受单纯形中的另一个点。[或者在下面的步骤 7 中，此算法会更改值在 f(x(1)) 上方的所有 n 个点。]
生成反射点
r = 2m – x(n + 1)， (1)
其中
m = Σx(i)/n, i = 1...n， (2)
并计算 f(r)。
如果 f(x(1)) ≤ f(r) < f(x(n))，则接受 r 并终止此迭代。反射
如果 f(r) < f(x(1))，则计算延伸点 s
s = m + 2(m – x(n + 1))， (3)
并计算 f(s)。
1. 如果 f(s) < f(r)，接受 s 并终止迭代。扩展
2. 否则，接受 r 并终止迭代。反射
如果 f(r) ≥ f(x(n))，则在 m 和 x(n + 1) 或 r（取目标函数值较低者）之间执行收缩。
1. 如果 f(r) < f(x(n + 1))（即 r 优于 x(n + 1)），则计算
  c = m + (r – m)/2 (4)
  并计算 f(c)。如果 f(c) < f(r)，则接受 c 并终止迭代。外收缩
  否则，继续执行步骤 7（收缩）。
2. 如果 f(r) ≥ f(x(n + 1))，则计算
  cc = m + (x(n + 1) – m)/2 (5)
  并计算 f(cc)。如果 f(cc) < f(x(n + 1))，则接受 cc 并终止迭代。内收缩
  否则，继续执行步骤 7（收缩）。
计算 n 点
v(i) = x(1) + (x(i) – x(1))/2 (6)
并计算 f(v(i))，i = 2,...,n + 1。下一迭代中的单纯形为 x(1), v(2),...,v(n + 1)。收缩

下图显示了 fminsearch 可在此过程中计算的点以及每种可能的新单纯形。原始单纯形采用粗体边框。迭代将在符合停止条件之前继续运行。

Graphical representation of fminsearch algorithm showing reflection, expansion, contraction, and shrinking points.

参考

[1] Lagarias, J. C., J. A. Reeds, M. H. Wright, and P. E. Wright. “Convergence Properties of the Nelder-Mead Simplex Method in Low Dimensions.” SIAM Journal of Optimization, Vol. 9, Number 1, 1998, pp. 112–147.