checkGradients
语法
说明
除了前面语法中的任何输入参量组合之外,valid = checkGradients(___,Name=Value)
示例
本例末尾的 rosen 函数计算二维变量 x 的 Rosenbrock 目标函数及其梯度。
检查 rosen 中计算的梯度是否与点 [2,4] 附近的有限差分近似相匹配。
x0 = [2,4]; valid = checkGradients(@rosen,x0)
valid = logical
1
function [f,g] = rosen(x) f = 100*(x(1) - x(2)^2)^2 + (1 - x(2))^2; if nargout > 1 g(1) = 200*(x(1) - x(2)^2); g(2) = -400*x(2)*(x(1) - x(2)^2) - 2*(1 - x(2)); end end
本例末尾的 vecrosen 函数以最小二乘形式计算 Rosenbrock 目标函数及其雅可比矩阵(梯度)。
检查 vecrosen 中计算的梯度是否与点 [2,4] 附近的有限差分近似相匹配。
x0 = [2,4]; valid = checkGradients(@vecrosen,x0)
valid = logical
1
function [f,g] = vecrosen(x) f = [10*(x(1) - x(2)^2),1-x(1)]; if nargout > 1 g = zeros(2); % Allocate g g(1,1) = 10; % df(1)/dx(1) g(1,2) = -20*x(2); % df(1)/dx(2) g(2,1) = -1; % df(2)/dx(1) g(2,2) = 0; % df(2)/dx(2) end end
本例末尾的 rosen 函数计算二维变量 x 的 Rosenbrock 目标函数及其梯度。
对于一些初始点,默认的正向有限差分导致 checkGradients 错误地指示 rosen 函数具有不正确的梯度。要查看结果详情,请将 Display 选项设置为 "on"。
x0 = [0,0];
valid = checkGradients(@rosen,x0,Display="on")____________________________________________________________ Objective function derivatives: Maximum relative difference between supplied and finite-difference derivatives = 1.48826e-06. Supplied derivative element (1,1): -0.126021 Finite-difference derivative element (1,1): -0.126023 checkGradients failed. Supplied derivative and finite-difference approximation are not within 'Tolerance' (1e-06). ____________________________________________________________
valid = logical
0
checkGradients 报告不匹配,小数点后第六位相差刚好超过 1。使用中心有限差分并再次检查。
opts = optimoptions("fmincon",FiniteDifferenceType="central"); valid = checkGradients(@rosen,x0,opts,Display="on")
____________________________________________________________ Objective function derivatives: Maximum relative difference between supplied and finite-difference derivatives = 1.29339e-11. checkGradients successfully passed. ____________________________________________________________
valid = logical
1
中心有限差分通常更准确。checkGradients 报告称梯度和中心有限差分近似匹配到小数点后约 11 位。
function [f,g] = rosen(x) f = 100*(x(1) - x(2)^2)^2 + (1 - x(2))^2; if nargout > 1 g(1) = 200*(x(1) - x(2)^2); g(2) = -400*x(2)*(x(1) - x(2)^2) - 2*(1 - x(2)); end end
此示例末尾的 tiltellipse 函数施加了约束,即二维变量 x 被限制在倾斜椭圆的内部
.
将椭圆可视化。
f = @(x,y) x.*y/2+(x+2).^2+(y-2).^2/2-2; fcontour(f,LevelList=0) axis([-6 0 -1 7])
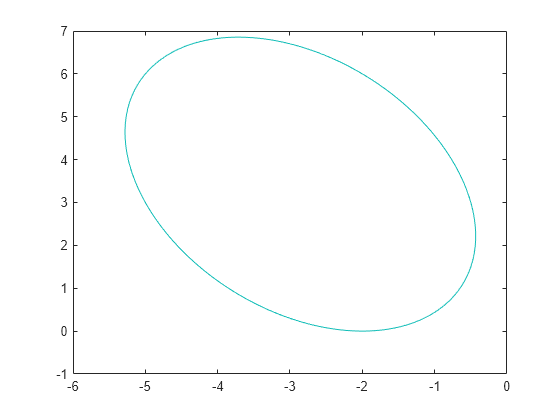
检查这个非线性不等式约束函数的梯度。
x0 = [-2,6]; valid = checkGradients(@tiltellipse,x0,IsConstraint=true)
valid = 1×2 logical array
1 1
function [c,ceq,gc,gceq] = tiltellipse(x) c = x(1)*x(2)/2 + (x(1) + 2)^2 + (x(2)- 2)^2/2 - 2; ceq = []; if nargout > 2 gc = [x(2)/2 + 2*(x(1) + 2); x(1)/2 + x(2) - 2]; gceq = []; end end
此示例末尾的 fungrad 函数正确计算了最小二乘目标某些分量的梯度,但错误地计算了其他成分的梯度。
检查 checkGradients 的第二个输出,查看哪些分量在点 [2,4] 处匹配不太好。要查看结果详情,请将 Display 选项设置为 "on"。
x0 = [2,4];
[valid,err] = checkGradients(@fungrad,x0,Display="on")____________________________________________________________ Objective function derivatives: Maximum relative difference between supplied and finite-difference derivatives = 0.749797. Supplied derivative element (3,2): 19.9838 Finite-difference derivative element (3,2): 5 checkGradients failed. Supplied derivative and finite-difference approximation are not within 'Tolerance' (1e-06). ____________________________________________________________
valid = logical
0
err = struct with fields:
Objective: [3×2 double]
输出表明元素 [3,2] 不正确。但这是唯一的问题吗?检查 err.Objective 并查找远离 0 的条目。
err.Objective
ans = 3×2
0.0000 0.0000
0.0000 0
0.5000 0.7498
导数的 [3,1] 和 [3,2] 元素都是不正确的。本示例末尾的 fungrad2 函数可纠正错误。
[valid,err] = checkGradients(@fungrad2,x0,Display="on")____________________________________________________________ Objective function derivatives: Maximum relative difference between supplied and finite-difference derivatives = 2.2338e-08. checkGradients successfully passed. ____________________________________________________________
valid = logical
1
err = struct with fields:
Objective: [3×2 double]
err.Objective
ans = 3×2
10-7 ×
0.2234 0.0509
0.0003 0
0.0981 0.0042
梯度近似和有限差分近似之间的所有差异在数量级上均小于 1e-7。
以下代码创建 fungrad 辅助函数。
function [f,g] = fungrad(x) f = [10*(x(1) - x(2)^2),1 - x(1),5*(x(2) - x(1)^2)]; if nargout > 1 g = zeros(3,2); g(1,1) = 10; g(1,2) = -20*x(2); g(2,1) = -1; g(3,1) = -20*x(1); g(3,2) = 5*x(2); end end
以下代码创建 fungrad2 辅助函数。
function [f,g] = fungrad2(x) f = [10*(x(1) - x(2)^2),1 - x(1),5*(x(2) - x(1)^2)]; if nargout > 1 g = zeros(3,2); g(1,1) = 10; g(1,2) = -20*x(2); g(2,1) = -1; g(3,1) = -10*x(1); g(3,2) = 5; end end
当您提供梯度计算函数时,非线性最小二乘求解器(如 lsqcurvefit)可以更快、更可靠地运行。然而,与其它求解器相比,lsqcurvefit 求解器在检查梯度时语法略有不同。
拟合问题和 checkGradient 语法
要检查 lsqcurvefit 梯度,不要将初始点 x0 作为数组传递,而是传递元胞数组 {x0,xdata}。例如,对于响应函数 ,从模型中创建添加了噪声的数据 ydata。响应函数为 fitfun。
function [F,J] = fitfun(x,xdata) F = x(1) + x(2)*exp(-x(3)*xdata); if nargout > 1 J = [ones(size(xdata)) exp(-x(3)*xdata) -xdata.*x(2).*exp(-x(3)*xdata)]; end end
生成 xdata 作为从 0 到 10 的随机点,并将 ydata 作为响应加上添加的噪声。
a = 2;
b = 5;
c = 1/15;
N = 100;
rng default
xdata = 10*rand(N,1);
fun = @fitfun;
ydata = fun([a,b,c],xdata) + randn(N,1)/10;检查响应函数在点 [a,b,c] 的梯度是否正确。
[valid,err] = checkGradients(@fitfun,{[a b c] xdata})valid = logical
1
err = struct with fields:
Objective: [100×3 double]
您可以安全地使用提供的目标梯度。将所有参数的下界设置为 0,无上界。
options = optimoptions("lsqcurvefit",SpecifyObjectiveGradient=true);
lb = zeros(1,3);
ub = [];
[sol,res,~,eflag,output] = lsqcurvefit(fun,[1 2 1],xdata,ydata,lb,ub,options)Local minimum possible. lsqcurvefit stopped because the final change in the sum of squares relative to its initial value is less than the value of the function tolerance. <stopping criteria details>
sol = 1×3
2.5872 4.4376 0.0802
res = 1.0096
eflag = 3
output = struct with fields:
firstorderopt: 4.4156e-06
iterations: 25
funcCount: 26
cgiterations: 0
algorithm: 'trust-region-reflective'
stepsize: 1.8029e-04
message: 'Local minimum possible.↵↵lsqcurvefit stopped because the final change in the sum of squares relative to ↵its initial value is less than the value of the function tolerance.↵↵<stopping criteria details>↵↵Optimization stopped because the relative sum of squares (r) is changing↵by less than options.FunctionTolerance = 1.000000e-06.'
bestfeasible: []
constrviolation: []
lsqcurvefit 中的非线性约束函数
非线性约束函数所需的语法与 lsqcurvefit 目标函数的语法不同。具有梯度的非线性约束函数具有以下形式:
function [c,ceq,gc,gceq] = ccon(x) c = ... ceq = ... if nargout > 2 gc = ... gceq = ... end end
梯度表达式的大小必须为 NxNc,其中 N 是问题变量的数量,Nc 是约束函数的数量。例如,下面的 ccon 函数只有一个非线性不等式约束。因此,对于这个包含三个变量的方程,该函数返回一个 3×1 的梯度。
function [c,ceq,gc,gceq] = ccon(x) ceq = []; c = x(1)^2 + x(2)^2 + 1/x(3)^2 - 50; if nargout > 2 gceq = []; gc = zeros(3,1); % Gradient is a column vector gc(1) = 2*x(1); gc(2) = 2*x(2); gc(3) = -2/x(3)^3; end end
检查函数 ccon 在点 [a,b,c] 返回的梯度是否正确。
[valid,err] = checkGradients(@ccon,[a b c],IsConstraint=true)
valid = 1×2 logical array
1 1
err = struct with fields:
Inequality: [3×1 double]
Equality: []
要使用约束梯度,请将选项设置为使用梯度函数,然后使用非线性约束再次求解问题。
options.SpecifyConstraintGradient = true; [sol2,res2,~,eflag2,output2] = lsqcurvefit(@fitfun,[1 2 1],xdata,ydata,lb,ub,[],[],[],[],@ccon,options)
Local minimum found that satisfies the constraints. Optimization completed because the objective function is non-decreasing in feasible directions, to within the value of the optimality tolerance, and constraints are satisfied to within the value of the constraint tolerance. <stopping criteria details>
sol2 = 1×3
4.4436 2.8548 0.2127
res2 = 2.2623
eflag2 = 1
output2 = struct with fields:
iterations: 15
funcCount: 22
constrviolation: 0
stepsize: 1.7914e-06
algorithm: 'interior-point'
firstorderopt: 3.3350e-06
cgiterations: 0
message: 'Local minimum found that satisfies the constraints.↵↵Optimization completed because the objective function is non-decreasing in ↵feasible directions, to within the value of the optimality tolerance,↵and constraints are satisfied to within the value of the constraint tolerance.↵↵<stopping criteria details>↵↵Optimization completed: The relative first-order optimality measure, 1.621619e-07,↵is less than options.OptimalityTolerance = 1.000000e-06, and the relative maximum constraint↵violation, 0.000000e+00, is less than options.ConstraintTolerance = 1.000000e-06.'
bestfeasible: [1×1 struct]
残差 res2 是残差 res 的两倍以上,而后者没有非线性约束。该结果表明,非线性约束使解远离无约束的最小值。
绘制有和没有非线性约束的解。
scatter(xdata,ydata) hold on scatter(xdata,fitfun(sol,xdata),"x") hold off xlabel("x") ylabel("y") legend("Data","Fitted") title("Data and Fitted Response, No Constraint")

figure scatter(xdata,ydata) hold on scatter(xdata,fitfun(sol2,xdata),"x") hold off xlabel("x") ylabel("y") legend("Data","Fitted with Constraint") title("Data and Fitted Response with Constraint")

输入参数
要检查的函数,指定为函数句柄。
如果
fun表示目标函数,则fun必须具有以下签名。[fval,grad] = fun(x)
checkGradients将grad(x)的值与x0附近点x的有限差分近似值进行比较。比较公式为其中
grad表示梯度函数的值,grad_fd表示有限差分近似的值。checkGradients逐个分量执行此除法。如果
fun表示最小二乘目标,则fun是一个向量,而grad(x)则是一个表示fun的雅可比矩阵的矩阵。如果
fun返回由m个分量组成的数组且x包含n个元素,其中n是x0的元素数,则雅可比J是m×n矩阵,其中J(i,j)是F(i)关于x(j)的偏导数。(雅可比值J是F的梯度的转置。)如果
fun表示非线性约束,则fun必须具有以下签名。[c,ceq,gc,gceq] = fun(x)
c表示非线性不等式约束。求解器尝试实现c <= 0。c输出可以是任意长度的向量。ceq表示非线性等式约束。求解器尝试实现ceq = 0。ceq输出可以是任意长度的向量。gc表示非线性不等式约束的梯度。梯度的大小应为NxNc,其中N为问题变量的数量,Nc为c的元素数量。gceq表示非线性等式约束的梯度。梯度的大小应为NxNceq,其中N为问题变量的数量,Nceq为ceq的元素数量。
数据类型: function_handle
检查梯度的位置,对于除 lsqcurvefit 之外的所有求解器指定为双精度数组。对于 lsqcurvefit,x0 是 1×2 元胞数组 {x0array,xdata}。
checkGradients 检查指定 x0 附近点的梯度。函数为 x0 添加一个小的随机方向,绝对值不超过 1e-3。这种扰动试图保护检查,以防止由于取消而导致不正确的梯度函数通过的点。
示例: randn(5,1)
数据类型: double
复数支持: 是
有限差分选项,指定为 optimoptions 的输出。以下选项影响有限差分。
| 选项 | 描述 |
|---|---|
FiniteDifferenceStepSize | 有限差分的标量或向量步长因子。当您将
sign′(x) = sign(x)(例外是 sign′(0) = 1)。中心有限差分是
FiniteDifferenceStepSize 扩展为向量。对于正向有限差分,默认值为 sqrt(eps);对于中心有限差分,默认值为 eps^(1/3)。 |
FiniteDifferenceType | 用于估计梯度的有限差分要么是 |
TypicalX | 典型的 |
| DiffMaxChange(不鼓励) | 有限差分梯度变量的最大变化(正标量)。默认值为 |
| DiffMinChange(不鼓励) | 有限差分梯度变量的最小变化(非负标量)。默认值为 |
示例: optimoptions("fmincon",FiniteDifferenceStepSize=1e-4)
名称-值参数
将可选参量对组指定为 Name1=Value1,...,NameN=ValueN,其中 Name 是参量名称,Value 是对应的值。名称-值参量必须出现在其他参量之后,但对各个参量对组的顺序没有要求。
在 R2021a 之前,使用逗号分隔每个名称和值,并用引号将 Name 引起来。
示例: IsConstraint=true,Tolerance=5e-4
输出参量
梯度和有限差分近似之间的相对差异,以结构体形式返回。对于目标函数,字段名称是 Objective。对于非线性约束函数,字段名称为 Inequality(对应 c)和 Equality(对应 ceq)。err 的每个分量都具有与 fun 提供的导数相同的形状。
详细信息
在初始点附近估计的梯度或雅可比矩阵与提供的导数不匹配,在默认容差 1e-6 范围内,或对于 checkGradients 函数,在指定的 Tolerance 值范围内。
通常,这种失败意味着您的目标或非线性约束函数的导数计算不正确。请再次检查指示的导数。
有时,对导数的有限差分逼近的准确性不足,从而导致失败。当函数(目标或非线性约束)的二阶导数具有较大幅值时,会出现这种不准确性。当使用默认
'forward'有限差分时也可能发生这种情况,这种有限差分比'central'有限差分准确性差,但速度更快。如果您认为导函数是正确的,请尝试以下一种或两种方法,看看CheckGradients是否能通过:将
FiniteDifferenceType选项设置为'central'。将
FiniteDifferenceStepSize选项设置为一个小值,如1e-10。
在初始点附近的随机点检查导数。因此,当不同邻近点具有不同检查结果时,梯度检查可能会随机通过或失败。
有关详细信息,请参阅检查梯度或雅可比矩阵的有效性。
版本历史记录
在 R2023b 中推出
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.
选择网站
选择网站以获取翻译的可用内容,以及查看当地活动和优惠。根据您的位置,我们建议您选择:。
您也可以从以下列表中选择网站:
如何获得最佳网站性能
选择中国网站(中文或英文)以获得最佳网站性能。其他 MathWorks 国家/地区网站并未针对您所在位置的访问进行优化。
美洲
- América Latina (Español)
- Canada (English)
- United States (English)
欧洲
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)