lsqnonlin

x = lsqnonlin(fun,x0,lb,ub) 对 x 中的设计变量定义一组下界和上界，使解始终在 lb ≤ x ≤ ub 范围内。您可以通过指定 lb(i) = ub(i) 来修复解分量 x(i)。

注意

如果问题的指定输入边界不一致，则输出 x 为 x0，输出 resnorm 和 residual 为 []。

违反边界 lb ≤ x ≤ ub 的 x0 的分量将重置为位于由边界定义的框内。遵守边界的分量不会更改。

x = lsqnonlin(fun,x0,lb,ub,A,b,Aeq,beq) 要求解满足以下线性约束

A x ≤ b

Aeq x = beq.

x = lsqnonlin(fun,x0,lb,ub,A,b,Aeq,beq,nonlcon) 要求解满足 nonlcon(x) 函数中的非线性约束。nonlcon 返回两个输出，即 c 和 ceq。求解器尝试满足以下约束

c ≤ 0

ceq = 0.

x = lsqnonlin(fun,x0,lb,ub,options) 和 x = lsqnonlin(fun,x0,lb,ub,A,b,Aeq,beq,nonlcon,options) 使用 options 中指定的优化选项执行最小化。使用 optimoptions 可设置这些选项。如果参量不存在，则为 lb 和 ub 及其他输入参量传递空矩阵。

x = lsqnonlin(problem) 求 problem 的最小值，它是 problem 中所述的一个结构体。

对于任何输入参量，[x,resnorm] = lsqnonlin(___) 返回在 x 处的残差的 2-范数平方值：sum(fun(x).^2)。

[x,resnorm,residual,exitflag,output] = lsqnonlin(___) 还返回在解 x 处的残差 fun(x) 的值、描述退出条件的值 exitflag，以及包含优化过程信息的结构体 output。

[x,resnorm,residual,exitflag,output,lambda,jacobian] = lsqnonlin(___) 还返回结构体 lambda（其字段包含在解 x 处的拉格朗日乘数），以及 fun 在解 x 处的雅可比矩阵。

示例

拟合简单指数

对数据进行简单的指数衰减曲线拟合。

从添加了噪声的指数衰减模型生成数据。模型是

$y = \exp (- 1.3 t) + ε,$

其中 $t$ 的范围是从 0 到 3， $ε$ 是均值为 0、标准差为 0.05 的正态分布噪声。

rng default % for reproducibility
d = linspace(0,3);
y = exp(-1.3*d) + 0.05*randn(size(d));

问题表述为：给定数据（d、y），求出与数据拟合最佳的指数衰减率。

创建一个匿名函数，该函数接受指数衰减率 $r$ 的值作为输入，并返回采用该衰减率的模型与数据之差组成的向量。

fun = @(r)exp(-d*r)-y;

找到最佳衰减率的值。任意选择一个初始估计值 x0 = 4。

x0 = 4;
x = lsqnonlin(fun,x0)

Local minimum possible.

lsqnonlin stopped because the final change in the sum of squares relative to 
its initial value is less than the value of the function tolerance.

<stopping criteria details>

x = 
1.2645

绘制数据和最佳拟合指数曲线。

plot(d,y,'ko',d,exp(-x*d),'b-')
legend('Data','Best fit')
xlabel('t')
ylabel('exp(-tx)')

Figure contains an axes object. The axes object with xlabel t, ylabel exp(-tx) contains 2 objects of type line. One or more of the lines displays its values using only markers These objects represent Data, Best fit.

拟合具有边界约束的问题

当某些拟合参数有边界时，找到最佳拟合模型。

找到合适的中心化参数 $b$ 和缩放参数 $a$ ，以便以下函数

$a \exp (- t) \exp (- \exp (- (t - b)))$

最好地拟合以下标准正态密度分布：

$\frac{1}{\sqrt{2 π}} \exp (- t^{2} / 2) .$

创建数据点组成的向量 t，以及在这些点上的对应正态密度。

t = linspace(-4,4);
y = 1/sqrt(2*pi)*exp(-t.^2/2);

创建一个缩放参数 $a$ 为 x(1) 且中心化参数 $b$ 为 x(2) 的函数，来计算中心化并缩放的函数与正态 y 之间的差。

fun = @(x)x(1)*exp(-t).*exp(-exp(-(t-x(2)))) - y;

从 x0 = [1/2,0] 开始寻找最佳拟合，缩放参数 $a$ 的值介于 1/2 和 3/2 之间，中心化参数 $b$ 的值介于 -1 和 3 之间。

lb = [1/2,-1];
ub = [3/2,3];
x0 = [1/2,0];
x = lsqnonlin(fun,x0,lb,ub)

Local minimum possible.

lsqnonlin stopped because the final change in the sum of squares relative to 
its initial value is less than the value of the function tolerance.

<stopping criteria details>

x = 1×2

    0.8231   -0.2444

绘制这两个函数来查看拟合的质量。

plot(t,y,'r-',t,fun(x)+y,'b-')
xlabel('t')
legend('Normal density','Fitted function')

Figure contains an axes object. The axes object with xlabel t contains 2 objects of type line. These objects represent Normal density, Fitted function.

具有线性约束的最小二乘

以下列目标函数为例（求平方和）：

$\sum_{k = 1}^{10} {(2 + 2 k + \exp (k x_{1}) + 2 \exp (2 k x_{2}^{2}))}^{2} .$

此目标函数的代码在此示例末尾显示为 myfun 函数。

在满足线性约束 $x_{1} \leq \frac{x_{2}}{2}$ 的条件下最小化此函数。将此约束编写为 $x_{1} - \frac{x_{2}}{2} \leq 0$ 。

A = [1 -1/2];
b = 0;

施加边界 $x_{1} \geq 0$ 、 $x_{2} \geq 0$ 、 $x_{1} \leq 2$ 和 $x_{2} \leq 4$ 。

lb = [0 0];
ub = [2 4];

从点 x0 = [0.3 0.4] 启动优化过程。

x0 = [0.3 0.4];

此问题没有线性等式约束。

Aeq = [];
beq = [];

运行优化。

x = lsqnonlin(@myfun,x0,lb,ub,A,b,Aeq,beq)

Local minimum found that satisfies the constraints.

Optimization completed because the objective function is non-decreasing in 
feasible directions, to within the value of the optimality tolerance,
and constraints are satisfied to within the value of the constraint tolerance.

<stopping criteria details>

x = 1×2

    0.1695    0.3389

function F = myfun(x)
k = 1:10;
F = 2 + 2*k - exp(k*x(1)) - 2*exp(2*k*(x(2)^2));
end

具有非线性约束的非线性最小二乘

以下列目标函数为例（求平方和）：

$\sum_{k = 1}^{10} {(2 + 2 k + \exp (k x_{1}) + 2 \exp (2 k x_{2}^{2}))}^{2} .$

此目标函数的代码在此示例末尾显示为 myfun 函数。

在满足非线性约束 $\sin (x_{1}) \leq \cos (x_{2})$ 的条件下最小化此函数。此非线性约束函数的代码在此示例末尾显示为 nlcon 函数。

施加边界 $x_{1} \geq 0$ 、 $x_{2} \geq 0$ 、 $x_{1} \leq 2$ 和 $x_{2} \leq 4$ 。

lb = [0 0];
ub = [2 4];

从点 x0 = [0.3 0.4] 启动优化过程。

x0 = [0.3 0.4];

该问题没有线性约束。

A = [];
b = [];
Aeq = [];
beq = [];

运行优化。

x = lsqnonlin(@myfun,x0,lb,ub,A,b,Aeq,beq,@nlcon)

Local minimum found that satisfies the constraints.

Optimization completed because the objective function is non-decreasing in 
feasible directions, to within the value of the optimality tolerance,
and constraints are satisfied to within the value of the constraint tolerance.

<stopping criteria details>

x = 1×2

    0.2133    0.3266

function F = myfun(x)
k = 1:10;
F = 2 + 2*k - exp(k*x(1)) - 2*exp(2*k*(x(2)^2));
end

function [c,ceq] = nlcon(x)
ceq = [];
c = sin(x(1)) - cos(x(2));
end

使用非默认选项执行非线性最小二乘运算

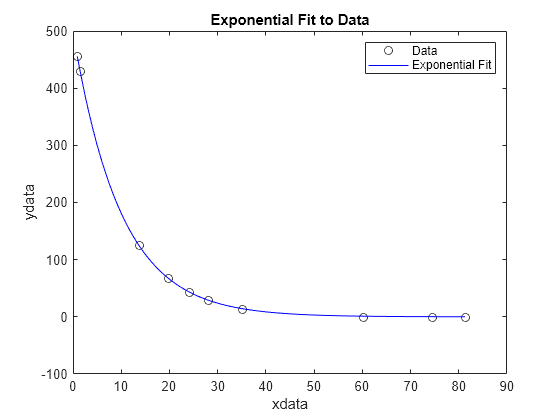
比较使用不同 lsqnonlin 算法求解数据拟合问题的结果。

假设您有观测时间数据 xdata 和观测响应数据 ydata，并且要求得参数 $x (1)$ 和 $x (2)$ 以拟合以下形式的模型

$ydata = x (1) \exp (x (2) xdata) .$

输入观测时间和响应。

xdata = ...
 [0.9 1.5 13.8 19.8 24.1 28.2 35.2 60.3 74.6 81.3];
ydata = ...
 [455.2 428.6 124.1 67.3 43.2 28.1 13.1 -0.4 -1.3 -1.5];

创建简单的指数衰减模型。该模型计算预测值和观测值之间的差组成的向量。

fun = @(x)x(1)*exp(x(2)*xdata)-ydata;

以 x0 = [100,-1] 为起点拟合模型。首先，使用默认的 'trust-region-reflective' 算法。

x0 = [100,-1];
options = optimoptions(@lsqnonlin,'Algorithm','trust-region-reflective');
x = lsqnonlin(fun,x0,[],[],options)

Local minimum possible.

lsqnonlin stopped because the final change in the sum of squares relative to 
its initial value is less than the value of the function tolerance.

<stopping criteria details>

x = 1×2

  498.8309   -0.1013

使用 'levenberg-marquardt' 算法查看是否有任何不同。

options.Algorithm = 'levenberg-marquardt';
x = lsqnonlin(fun,x0,[],[],options)

Local minimum possible.
lsqnonlin stopped because the relative size of the current step is less than
the value of the step size tolerance.

<stopping criteria details>

x = 1×2

  498.8309   -0.1013

这两种算法找到相同的解。绘制解和数据。

plot(xdata,ydata,'ko')
hold on
tlist = linspace(xdata(1),xdata(end));
plot(tlist,x(1)*exp(x(2)*tlist),'b-')
xlabel xdata
ylabel ydata
title('Exponential Fit to Data')
legend('Data','Exponential Fit')
hold off

Figure contains an axes object. The axes object with title Exponential Fit to Data, xlabel xdata, ylabel ydata contains 2 objects of type line. One or more of the lines displays its values using only markers These objects represent Data, Exponential Fit.

非线性最小二乘解和残差范数

求最小化下式的 $x$

$\sum_{k = 1}^{10} {(2 + 2 k - e^{k x_{1}} - e^{k x_{2}})}^{2}$ ,

并求最小平方和的值。

由于 lsqnonlin 假设平方和不在用户定义的函数中显式得出，因此传递给 lsqnonlin 的函数应计算向量值函数

$F_{k} (x) = 2 + 2 k - e^{k x_{1}} - e^{k x_{2}}$ ,

其中 $k = 1$ 到 $10$ （即 $F$ 应包含 $10$ 个分量）。

myfun 函数位于此示例末尾，它用于计算包含 10 个分量的向量 F。

从 x0 = [0.3,0.4] 点开始，求最小化点和对应的最小值。

x0 = [0.3,0.4];
[x,resnorm] = lsqnonlin(@myfun,x0)

Local minimum possible.
lsqnonlin stopped because the size of the current step is less than
the value of the step size tolerance.

<stopping criteria details>

x = 1×2

    0.2578    0.2578

resnorm = 
124.3622

resnorm 输出是残差范数的平方，或函数值的平方和。

以下函数计算向量值目标函数。

function F = myfun(x)
k = 1:10;
F = 2 + 2*k-exp(k*x(1))-exp(k*x(2));
end

检查求解过程

在求解过程发生时和发生后都对其进行检查（通过将 Display 选项设置为 'iter' 在发生时进行检查，通过检查 output 结构体在发生后进行检查）。

假设您有观测时间数据 xdata 和观测响应数据 ydata，并且要求得参数 $x (1)$ 和 $x (2)$ 以拟合以下形式的模型

$ydata = x (1) \exp (x (2) xdata) .$

输入观测时间和响应。

xdata = ...
 [0.9 1.5 13.8 19.8 24.1 28.2 35.2 60.3 74.6 81.3];
ydata = ...
 [455.2 428.6 124.1 67.3 43.2 28.1 13.1 -0.4 -1.3 -1.5];

创建简单的指数衰减模型。该模型计算预测值和观测值之间的差组成的向量。

fun = @(x)x(1)*exp(x(2)*xdata)-ydata;

以 x0 = [100,-1] 为起点拟合模型。通过将 Display 选项设置为 'iter' 来检查求解过程。获取 output 结构体以获取有关求解过程的详细信息。

x0 = [100,-1];
options = optimoptions('lsqnonlin','Display','iter');
[x,resnorm,residual,exitflag,output] = lsqnonlin(fun,x0,[],[],options);

                                            Norm of      First-order 
 Iteration  Func-count      Resnorm            step       optimality
     0          3            359677                         2.88e+04
Objective function returned Inf; trying a new point...
     1          6            359677         11.6976         2.88e+04      
     2          9            321395             0.5         4.97e+04      
     3         12            321395               1         4.97e+04      
     4         15            292253            0.25         7.06e+04      
     5         18            292253             0.5         7.06e+04      
     6         21            270350           0.125         1.15e+05      
     7         24            270350            0.25         1.15e+05      
     8         27            252777          0.0625         1.63e+05      
     9         30            252777           0.125         1.63e+05      
    10         33            243877         0.03125         7.48e+04      
    11         36            243660          0.0625          8.7e+04      
    12         39            243276          0.0625            2e+04      
    13         42            243174          0.0625         1.14e+04      
    14         45            242999           0.125          5.1e+03      
    15         48            242661            0.25         2.04e+03      
    16         51            241987             0.5         1.91e+03      
    17         54            240643               1         1.04e+03      
    18         57            237971               2         3.36e+03      
    19         60            232686               4         6.04e+03      
    20         63            222354               8          1.2e+04      
    21         66            202592              16         2.25e+04      
    22         69            166443              32         4.05e+04      
    23         72            106320              64         6.68e+04      
    24         75           28704.7             128         8.31e+04      
    25         78           89.7947         140.674         2.22e+04      
    26         81           9.57381         2.02599              684      
    27         84           9.50489       0.0619927             2.27      
    28         87           9.50489     0.000462261           0.0114      

Local minimum possible.

lsqnonlin stopped because the final change in the sum of squares relative to 
its initial value is less than the value of the function tolerance.

<stopping criteria details>

检查输出结构体以获得有关求解过程的详细信息。

output

output = struct with fields:
      firstorderopt: 0.0114
         iterations: 28
          funcCount: 87
       cgiterations: 0
          algorithm: 'trust-region-reflective'
           stepsize: 4.6226e-04
            message: 'Local minimum possible.↵↵lsqnonlin stopped because the final change in the sum of squares relative to ↵its initial value is less than the value of the function tolerance.↵↵<stopping criteria details>↵↵Optimization stopped because the relative sum of squares (r) is changing↵by less than options.FunctionTolerance = 1.000000e-06.'
       bestfeasible: []
    constrviolation: []

为便于比较，请将 Algorithm 选项设置为 'levenberg-marquardt'。

options.Algorithm = 'levenberg-marquardt';
[x,resnorm,residual,exitflag,output] = lsqnonlin(fun,x0,[],[],options);

                                        First-order                     Norm of 
 Iteration  Func-count      Resnorm      optimality       Lambda           step
     0           3           359677        2.88e+04         0.01
Objective function returned Inf; trying a new point...
     1          13           340761        3.91e+04       100000       0.280777
     2          16           304661        5.97e+04        10000       0.373146
     3          21           297292        6.55e+04        1e+06      0.0589933
     4          24           288240        7.57e+04       100000      0.0645444
     5          28           275407        1.01e+05        1e+06      0.0741266
     6          31           249954        1.62e+05       100000       0.094571
     7          36           245896        1.35e+05        1e+07      0.0133606
     8          39           243846        7.26e+04        1e+06      0.0094431
     9          42           243568        5.66e+04       100000      0.0082162
    10          45           243424        1.61e+04        10000     0.00777935
    11          48           243322         8.8e+03         1000      0.0673933
    12          51           242408         5.1e+03          100       0.675209
    13          54           233628        1.05e+04           10        6.59804
    14          57           169089        8.51e+04            1        54.6992
    15          60          30814.7        1.54e+05          0.1        196.939
    16          63          147.496           8e+03         0.01        129.795
    17          66          9.51503             117        0.001        9.96069
    18          69          9.50489          0.0714       0.0001       0.080486
    19          72          9.50489        5.23e-05        1e-05    5.07043e-05

Local minimum possible.
lsqnonlin stopped because the relative size of the current step is less than
the value of the step size tolerance.

<stopping criteria details>

'levenberg-marquardt' 经过较少迭代次数即实现收敛，但迭代次数与函数计算次数几乎相同：

output

output = struct with fields:
         iterations: 19
          funcCount: 72
           stepsize: 5.0704e-05
       cgiterations: []
      firstorderopt: 5.2319e-05
          algorithm: 'levenberg-marquardt'
            message: 'Local minimum possible.↵lsqnonlin stopped because the relative size of the current step is less than↵the value of the step size tolerance.↵↵<stopping criteria details>↵↵Optimization stopped because the relative norm of the current step, 1.016463e-07,↵is less than options.StepTolerance = 1.000000e-06.'
       bestfeasible: []
    constrviolation: []

输入参数

`fun` — 要最小化其平方和的函数
函数句柄 | 函数的名称

要最小化其平方和的函数，指定为函数句柄或函数名称。对于 'interior-point' 算法，fun 必须为函数句柄。fun 函数接受数组 x，并返回数组 F，即在 x 处计算的目标函数值。

注意

平方和不应显式得出。您的函数应返回由函数值组成的向量。请参阅示例。

函数 fun 可以指定为文件的函数句柄：

x = lsqnonlin(@myfun,x0)

其中 myfun 是一个 MATLAB^® 函数，例如

function F = myfun(x)
F = ...            % Compute function values at x

fun 也可以是匿名函数的函数句柄。

x = lsqnonlin(@(x)sin(x.*x),x0);

lsqnonlin 以 x0 参量的形状将 x 传递给目标函数。例如，如果 x0 是 5×3 数组，则 lsqnonlin 将 x 以 5×3 数组的形式传递给 fun。

如果雅可比矩阵也可以计算并且 'SpecifyObjectiveGradient' 选项为 true，设置如下

options = optimoptions('lsqnonlin','SpecifyObjectiveGradient',true)

则函数 fun 必须返回第二个输出参量，即在 x 处计算的雅可比值矩阵 J。通过检查 nargout 的值，当仅使用一个输出参量调用 fun 时（在优化算法只需 F 的值而不需要 J 的情况下），该函数可以避免计算 J。

function [F,J] = myfun(x)
F = ...          % Objective function values at x
if nargout > 1   % Two output arguments
   J = ...   % Jacobian of the function evaluated at x
end

如果 fun 返回由 m 个分量组成的数组且 x 包含 n 个元素，其中 n 是 x0 的元素数，则雅可比J 是 m×n 矩阵，其中 J(i,j) 是 F(i) 关于 x(j) 的偏导数。（雅可比值 J 是 F 的梯度的转置。）

示例: @(x)cos(x).*exp(-x)

数据类型: char | function_handle | string

`x0` — 初始点
实数向量 | 实数数组

初始点，指定为实数向量或实数数组。求解器使用 x0 中的元素数量和 x0 的大小来确定 fun 接受的变量数量和大小。

示例: x0 = [1,2,3,4]

数据类型: double

`lb` — 下界
实数向量 | 实数数组

下界，指定为实数向量或实数数组。如果 x0 中的元素数等于 lb 中的元素数，则 lb 指定

x(i) >= lb(i)（对于全部 i）。

如果 numel(lb) < numel(x0)，则 lb 指定

x(i) >= lb(i) (1 <= i <= numel(lb))。

如果 lb 的元素数少于 x0，求解器将发出警告。

示例: 要指定所有 x 分量为正，请使用 lb = zeros(size(x0))。

数据类型: single | double

`ub` — 上界
实数向量 | 实数数组

上界，指定为实数向量或实数数组。如果 x0 中的元素数等于 ub 中的元素数，则 ub 指定

x(i) <= ub(i)（对于全部 i）。

如果 numel(ub) < numel(x0)，则 ub 指定

x(i) <= ub(i) (1 <= i <= numel(ub))。

如果 ub 的元素数少于 x0，求解器将发出警告。

示例: 要指定 x 的所有分量小于 1，请使用 ub = ones(size(x0))。

数据类型: single | double

`A` — 线性不等式约束
实矩阵

线性不等式约束，指定为实矩阵。A 是 M×N 矩阵，其中 M 是不等式的数目，而 N 是变量的数目（x0 中的元素数）。对于大型问题，如果使用支持稀疏数据的算法，则可将 A 作为稀疏矩阵传递。请参阅稀疏性在优化算法中的应用。

A 以如下形式编写 M 个线性不等式

A*x <= b,

其中，x 是由 N 个变量组成的列向量 x(:)，b 是具有 M 个元素的列向量。

例如，假设有以下不等式：

x₁ +2x₂ ≤10
3x₁ +4x₂ ≤20
5x₁ +6x₂ ≤30，

通过输入以下约束来指定不等式。

A = [1,2;3,4;5,6];
b = [10;20;30];

示例: 要指定 x 分量总和等于或小于 1，请使用 A = ones(1,N) 和 b = 1。

数据类型: single | double

`b` — 线性不等式约束
实数向量

线性不等式约束，指定为实数向量。b 是与 A 矩阵相关的包含 M 个元素的向量。如果将 b 作为行向量传递，求解器会在内部将 b 转换为列向量 b(:)。

b 以如下形式编写 M 个线性不等式

A*x <= b,

其中，x 是由 N 个变量组成的列向量 x(:)，A 是大小为 M×N 的矩阵。

例如，假设有以下不等式：

x₁ + 2x₂ ≤ 10
3x₁ + 4x₂ ≤ 20
5x₁ + 6x₂ ≤ 30。

通过输入以下约束来指定不等式。

A = [1,2;3,4;5,6];
b = [10;20;30];

示例: 要指定 x 分量总和等于或小于 1，请使用 A = ones(1,N) 和 b = 1。

数据类型: single | double

`Aeq` — 线性等式约束
实矩阵

线性等式约束，指定为实矩阵。Aeq 是 Me×N 矩阵，其中 Me 是等式的数目，而 N 是变量的数目（x0 中的元素数）。对于大型问题，如果使用支持稀疏数据的算法，则可将 A 作为稀疏矩阵传递。请参阅稀疏性在优化算法中的应用。

Aeq 以如下形式编写 Me 个线性等式

Aeq*x = beq,

其中，x 是由 N 个变量组成的列向量 x(:)，beq 是具有 Me 个元素的列向量。

例如，假设有以下不等式：

x₁ +2x₂ +3x₃ =10
2x₁ +4x₂ + x₃ =20，

通过输入以下约束来指定不等式。

Aeq = [1,2,3;2,4,1];
beq = [10;20];

示例: 要指定 x 分量总和为 1，请使用 Aeq = ones(1,N) 和 beq = 1。

数据类型: single | double

`beq` — 线性等式约束
实数向量

线性等式约束，指定为实数向量。beq 是与 Aeq 矩阵相关的包含 Me 个元素的向量。如果将 beq 作为行向量传递，求解器会在内部将 beq 转换为列向量 beq(:)。

beq 以如下形式编写 Me 个线性等式

Aeq*x = beq,

其中，x 是由 N 个变量组成的列向量 x(:)，Aeq 是大小为 Me×N 的矩阵。

例如，请参考以下等式：

x₁ + 2x₂ + 3x₃ = 10
2x₁ + 4x₂ + x₃ = 20。

通过输入以下约束来指定等式。

Aeq = [1,2,3;2,4,1];
beq = [10;20];

示例: 要指定 x 分量总和为 1，请使用 Aeq = ones(1,N) 和 beq = 1。

数据类型: single | double

`nonlcon` — 非线性约束
函数句柄

非线性约束，指定为函数句柄。nonlcon 函数接受向量或数组 x，并返回两个数组 c(x) 和 ceq(x)。

c(x) 是由 x 处的非线性不等式约束组成的数组。lsqnonlin 尝试满足
对于 c 的所有项，有 c(x) <= 0。 (1)
ceq(x) 是由 x 处的非线性等式约束组成的数组。lsqnonlin 尝试满足
对于 ceq 的所有项，有 ceq(x) = 0。 (2)

例如，

x = lsqnonlin(@myfun,x0,lb,ub,A,b,Aeq,beq,@mycon,options)

其中 mycon 是一个 MATLAB 函数，例如

function [c,ceq] = mycon(x)
c = ...     % Compute nonlinear inequalities at x.
ceq = ...   % Compute nonlinear equalities at x.

如果约束的雅可比矩阵（导数）也可以计算且 SpecifyConstraintGradient 选项是 true，设置如下：

options = optimoptions('lsqnonlin','SpecifyConstraintGradient',true)

则 nonlcon 还必须在第三个和第四个输出参量中返回 GC（即 c(x) 的雅可比矩阵）和 GCeq（即 ceq(x) 的雅可比矩阵）。向量函数 F(x) 的雅可比矩阵 G(x) 是

$G_{i, j} (x) = \frac{\partial F_{i} (x)}{\partial x_{j}} .$

GC 和 GCeq 可以是稀疏或稠密矩阵。如果 GC 或 GCeq 较大，非零项相对较少，则通过将它们表示为稀疏矩阵，可以节省 'interior-point' 算法的运行时间和内存使用量。有关详细信息，请参阅非线性约束。

数据类型: function_handle

`options` — 优化选项
`optimoptions` 的输出 | `optimset` 返回的结构体

优化选项，指定为 optimoptions 的输出或 optimset 返回的结构体。

一些选项适用于所有算法，其他选项则与特定算法相关。有关详细信息，请参阅优化选项参考。

optimoptions 显示中缺少某些选项。这些选项在下表中以斜体显示。有关详细信息，请参阅查看优化选项。

所有算法
`Algorithm`	在 `'trust-region-reflective'`（默认值）、`'levenberg-marquardt'` 和 `'interior-point'` 之间进行选择。 `Algorithm` 选项指定算法使用的预设项。这只是一种预设项，因为每种算法都必须满足特定条件才能使用。对于信赖域反射算法，由 `fun` 返回的 `F` 的元素数必须至少与 `x` 的长度相同。只有 `'interior-point'` 算法才能求解具有线性或非线性约束的问题。如果您在问题中包含这些约束并且未指定算法，则求解器将自动切换到 `'interior-point'` 算法。`'interior-point'` 算法会调用 `fmincon` `'interior-point'` 算法的修正版本。有关选择算法的详细信息，请参阅选择算法。
CheckGradients	将用户提供的导数（目标或约束的梯度）与有限差分导数进行比较。选项是 `false`（默认值）或 `true`。对于 `optimset`，名称为 `DerivativeCheck`，值为 `'on'` 或 `'off'`。请参阅当前选项名称和旧选项名称。以后的版本中将会删除 `CheckGradients` 选项。要检查导数，请使用 `checkGradients` 函数。
Diagnostics	显示关于要最小化或求解的函数的诊断信息。选项是 `'off'`（默认值）或 `'on'`。
DiffMaxChange	有限差分梯度变量的最大变化（正标量）。默认值为 `Inf`。
DiffMinChange	有限差分梯度变量的最小变化（正标量）。默认值为 `0`。
`Display`	显示级别（请参阅迭代输出）： `'off'` 或 `'none'` 不显示输出。 `'iter'` 显示每次迭代的输出，并给出默认退出消息。 `'iter-detailed'` 显示每次迭代的输出，并给出带有技术细节的退出消息。 `'final'`（默认值）仅显示最终输出，并给出默认退出消息。 `'final-detailed'` 仅显示最终输出，并给出带有技术细节的退出消息。
`FiniteDifferenceStepSize`	有限差分的标量或向量步长因子。当您将 `FiniteDifferenceStepSize` 设置为向量 `v` 时，正向有限差分 `delta` 是 `delta = v.sign′(x).max(abs(x),TypicalX);` 其中 `sign′(x) = sign(x)`（例外是 `sign′(0) = 1`）。中心有限差分是 `delta = v.*max(abs(x),TypicalX);` 标量 `FiniteDifferenceStepSize` 扩展为向量。对于正向有限差分，默认值为 `sqrt(eps)`；对于中心有限差分，默认值为 `eps^(1/3)`。对于 `optimset`，名称是 `FinDiffRelStep`。请参阅当前选项名称和旧选项名称。
`FiniteDifferenceType`	用于估计梯度的有限差分是 `'forward'`（默认值）或 `'central'`（中心化）。`'central'` 需要两倍的函数计算次数，但应更准确。当同时估计这两种类型的有限差分时，该算法小心地遵守边界。因此，例如，为了避免在边界之外的某个点进行计算，它可能采取一个后向差分，而不是前向差分。对于 `optimset`，名称是 `FinDiffType`。请参阅当前选项名称和旧选项名称。
`FunctionTolerance`	函数值的终止容差，非负标量。默认值为 `1e-6`。请参阅容差和停止条件。对于 `optimset`，名称是 `TolFun`。请参阅当前选项名称和旧选项名称。
FunValCheck	检查函数值是否有效。当函数返回的值是 `complex`、`Inf` 或 `NaN` 时，`'on'` 显示错误。默认值 `'off'` 不显示错误。
`MaxFunctionEvaluations`	允许的最大函数计算次数，非负整数。对于 `'trust-region-reflective'` 算法，默认值为 `100numberOfVariables`；对于 `'levenberg-marquardt'` 算法，默认值为 `200numberOfVariables`；对于 `'interior-point'` 算法，默认值为 `3000`。请参阅容差和停止条件和迭代和函数计算次数。对于 `optimset`，名称是 `MaxFunEvals`。请参阅当前选项名称和旧选项名称。
`MaxIterations`	允许的最大迭代次数，非负整数。对于 `'trust-region-reflective'` 和 `'levenberg-marquardt'` 算法，默认值为 `400`；对于 `'interior-point'` 算法，默认值为 `1000`。请参阅容差和停止条件和迭代和函数计算次数。对于 `optimset`，名称是 `MaxIter`。请参阅当前选项名称和旧选项名称。
`OptimalityTolerance`	一阶最优性的终止容差（非负标量）。默认值为 `1e-6`。请参阅一阶最优性测度。 `'levenberg-marquardt'` 算法在内部使用 `1e-4` 乘以 `FunctionTolerance` 作为最优性容差（停止条件），而不使用 `OptimalityTolerance`。对于 `optimset`，名称是 `TolFun`。请参阅当前选项名称和旧选项名称。
`OutputFcn`	指定优化函数在每次迭代中调用的一个或多个用户定义的函数。传递函数句柄或函数句柄的元胞数组。默认值是“无”(`[]`)。请参阅输出函数和绘图函数语法。
`PlotFcn`	对算法执行过程中的各种进度测量值绘图，可以选择预定义的绘图，也可以自行编写绘图函数。传递名称、函数句柄或者由名称或函数句柄组成的元胞数组。对于自定义绘图函数，传递函数句柄。默认值是“无”(`[]`)： `'optimplotx'` 绘制当前点。 `'optimplotfunccount'` 绘制函数计数。 `'optimplotfval'` 绘制函数值。 `'optimplotresnorm'` 绘制残差范数。 `'optimplotstepsize'` 绘制步长。 `'optimplotfirstorderopt'` 绘制一阶最优性测度。自定义绘图函数使用与输出函数相同的语法。请参阅Optimization Toolbox 的输出函数和输出函数和绘图函数语法。对于 `optimset`，名称是 `PlotFcns`。请参阅当前选项名称和旧选项名称。
`SpecifyObjectiveGradient`	如果为 `false`（默认值），则求解器使用有限差分逼近雅可比矩阵。如果为 `true`，则对于目标函数，求解器使用用户定义的雅可比矩阵（在 `fun` 中定义）或雅可比矩阵信息（使用 `JacobMult` 时）。对于 `optimset`，名称为 `Jacobian`，值为 `'on'` 或 `'off'`。请参阅当前选项名称和旧选项名称。
`StepTolerance`	`x` 的终止容差，非负标量。对于 `'trust-region-reflective'` 和 `'levenberg-marquardt'` 算法，默认值为 `1e-6`；对于 `'interior-point'` 算法，默认值为 `1e-10`。请参阅容差和停止条件。对于 `optimset`，名称是 `TolX`。请参阅当前选项名称和旧选项名称。
`TypicalX`	典型的 `x` 值。`TypicalX` 中的元素数等于 `x0`（即起点）中的元素数。默认值为 `ones(numberofvariables,1)`。求解器使用 `TypicalX` 缩放有限差分来进行梯度估计。
`UseParallel`	当为 `true` 时，求解器以并行方式估计梯度。要禁用，请将其设置为默认值 `false`。请参阅并行计算。
信赖域反射算法
`JacobianMultiplyFcn`	雅可比矩阵乘法函数，指定为函数句柄。对于大规模结构问题，此函数计算雅可比矩阵乘积 `JY`、`J'Y` 或 `J'(JY)`，而并不实际构造 `J`。对于 `lsqnonlin`，函数的形式是 W = jmfun(Jinfo,Y,flag) 其中 `Jinfo` 包含有助于计算 `JY` （或 `J'Y` 或 `J'(JY)`）的数据。对于 `lsqcurvefit`，函数的形式是 W = jmfun(Jinfo,Y,flag,xdata) 其中 `xdata` 是在 `xdata` 参量中传递的数据。数据 `Jinfo` 是目标函数 `fun` 返回的第二个参量： [F,Jinfo] = fun(x) % or [F,Jinfo] = fun(x,xdata) `lsqnonlin` 传递数据 `Jinfo`、`Y`、`flag`，对于 `lsqcurvefit`，传递数据 `xdata`，然后函数 `jmfun` 计算指定结果。`Y` 是矩阵，其大小取决于 `flag` 的值。假设 `m` 指定目标函数 `fun` 的分量个数，并假设 `n` 指定 `x` 中问题变量的个数。雅可比矩阵的大小为 `m`×`n`，如 `fun` 中所述。`jmfun` 函数返回以下结果之一：如果 `flag == 0`，则 `W = J'(JY)` 和 `Y` 的大小为 `n`×`2`。如果 `flag > 0`，则 `W = JY` 和 `Y` 的大小为 `n`×`1`。如果 `flag < 0`，则 `W = J'Y` 和 `Y` 的大小为 `m`×`1`。在每种情况下，都不会显式形成 `J`。求解器使用 `Jinfo` 计算乘法。有关如何为 `jmfun` 所需的额外参数提供值的信息，请参阅传递额外参数。注意 `'SpecifyObjectiveGradient'` 必须设置为 `true`，求解器才能将 `Jinfo` 从 `fun` 传递到 `jmfun`。有关类似示例，请参阅使用密集结构 Hessian 和线性等式进行最小化和雅可比乘法函数与线性最小二乘法。对于 `optimset`，名称是 `JacobMult`。请参阅当前选项名称和旧选项名称。
JacobPattern	用于有限差分的雅可比矩阵稀疏模式。当 `fun(i)` 依赖 `x(j)` 时，设置 `JacobPattern(i,j) = 1`。否则，设置 `JacobPattern(i,j) = 0`。换句话说，如果存在 ∂`fun(i)`/∂`x(j)` ≠ 0，则 `JacobPattern(i,j) = 1`。如果在 `fun` 中不方便计算雅可比矩阵 `J`，但您可以确定（例如通过分析）`fun(i)` 何时取决于 `x(j)`，请使用 `JacobPattern`。当您给出 `JacobPattern` 时，求解器可以通过稀疏有限差分来逼近 `J`。如果结构未知，请不要设置 `JacobPattern`。默认行为是将 `JacobPattern` 视为由 1 组成的稠密矩阵。然后求解器在每次迭代中计算满有限差分逼近。对于大型问题，这可能会涉及高昂的计算成本，因此通常最好采用稀疏结构。
MaxPCGIter	PCG（预条件共轭梯度）迭代的最大次数，正标量。默认值为 `max(1,numberOfVariables/2)`。有关详细信息，请参阅大规模非线性最小二乘。
PrecondBandWidth	PCG 的预条件子上带宽，非负整数。`PrecondBandWidth` 的默认值是 `Inf`，这意味着使用直接分解（乔列斯基分解），而不是共轭梯度 (CG)。直接分解的计算成本较 CG 高，但所得的求解步质量更好。将 `PrecondBandWidth` 设置为 `0` 将使用对角预条件（上带宽为 0）。对于某些问题，中间带宽会减少 PCG 迭代的次数。
`SubproblemAlgorithm`	确定迭代步的计算方式。相比 `'cg'`，默认值 `'factorization'` 采用的迭代步较慢，但更准确。请参阅信赖域反射最小二乘。
TolPCG	PCG 迭代的终止容差，正标量。默认值为 `0.1`。
莱文贝格-马夸特算法
InitDamping	莱文贝格-马夸特参数的初始值，正标量。默认值是 `1e-2`。有关详细信息，请参阅莱文贝格-马夸特方法。
ScaleProblem	`'jacobian'` 有时可以改善缩放不当问题的收敛；默认值为 `'none'`。
内点算法
`BarrierParamUpdate`	指定 `fmincon` 如何更新障碍参数（请参阅 fmincon 内点算法）。选项包括： `'monotone'`（默认值） `'predictor-corrector'` 此选项会影响求解器的速度和收敛，但效果不容易预测。
`ConstraintTolerance`	约束违反值的容差，非负标量。默认值为 `1e-6`。请参阅容差和停止条件。对于 `optimset`，名称是 `TolCon`。请参阅当前选项名称和旧选项名称。
InitBarrierParam	初始障碍值，正标量。有时尝试高于默认值 `0.1` 的值可能会有所帮助，尤其是当目标或约束函数很大时。
`SpecifyConstraintGradient`	用户定义的非线性约束函数梯度。当设置为默认值 `false` 时，`lsqnonlin` 通过有限差分估计非线性约束的梯度。当设置为 `true` 时，`lsqnonlin` 预计约束函数有四个输出，如 `nonlcon` 中所述。对于 `optimset`，名称为 `GradConstr`，值为 `'on'` 或 `'off'`。请参阅当前选项名称和旧选项名称。
`SubproblemAlgorithm`	确定迭代步的计算方式。默认值 `'factorization'` 通常比 `'cg'`（共轭梯度）更快，但对于具有稠密黑塞矩阵的大型问题，`'cg'` 可能更快。请参阅fmincon 内点算法。对于 `optimset`，值为 `'cg'` 和 `'ldl-factorization'`。请参阅当前选项名称和旧选项名称。

示例: options = optimoptions('lsqnonlin','FiniteDifferenceType','central')

`problem` — 问题结构体
结构体

问题结构体，指定为含有以下字段的结构体：

字段名称	条目
`objective`	目标函数
`x0`	`x` 的初始点
`Aineq`	线性不等式约束的矩阵
`bineq`	线性不等式约束的向量
`Aeq`	线性等式约束的矩阵
`beq`	线性等式约束的向量
`lb`	由下界组成的向量
`ub`	由上界组成的向量
`nonlcon`	非线性约束函数
`solver`	`'lsqnonlin'`
`options`	用 `optimoptions` 创建的选项

您必须在 problem 结构体中至少提供 objective、x0、solver 和 options 字段。

数据类型: struct

输出参量

`x` — 解
实数向量 | 实数数组

解，以实数向量或实数数组形式返回。x 的大小与 x0 的大小相同。通常情况下，当 exitflag 为正时，x 是该问题的局部解。有关解质量的信息，请参阅求解成功后。

`resnorm` — 残差范数的平方
非负实数

残差范数的平方，以非负实数形式返回。resnorm 是在 x 处的残差的 2-范数平方：sum(fun(x).^2)。

`residual` — 在解处的目标函数值
数组

在解处的目标函数值，以数组形式返回。一般来说，residual = fun(x)。

`exitflag` — 求解器停止的原因
整数

求解器停止的原因，以整数形式返回。

`1`	函数收敛于解 `x`。
`2`	`x` 中的变化小于指定容差，或 `x` 处的雅可比矩阵未定义。
`3`	残差中的变化小于指定的容差。
`4`	搜索方向的相对量级小于步长容差。
`0`	迭代次数超过 `options.MaxIterations` 或函数计算次数超过 `options.MaxFunctionEvaluations`。
`-1`	绘图函数或输出函数停止了求解器。
`-2`	找不到可行点。边界 `lb` 和 `ub` 不一致，或求解器已在不可行点处停止。

`output` — 有关优化过程的信息
结构体

有关优化过程的信息，以包含下列字段的结构体形式返回：

`firstorderopt`	一阶最优性的测度
`iterations`	执行的迭代次数
`funcCount`	函数计算的次数
`cgiterations`	PCG 迭代总次数（适用于 `'trust-region-reflective'` 和 `'interior-point'` 算法）
`stepsize`	`x` 中的最终位移
`constrviolation`	约束函数的最大值（`'interior-point'` 算法）
`bestfeasible`	遇到的最佳（目标函数值最低）可行点（`'interior-point'` 算法）。具有以下字段的结构体： `x` `fval` `firstorderopt` `constrviolation` 如果找不到可行点，则 `bestfeasible` 字段为空。为此，当约束函数的最大值不超过 `options.ConstraintTolerance` 时，点是可行的。由于各种原因，`bestfeasible` 点可能与返回的解点 `x` 不同。有关示例，请参阅获取最佳可行点。
`algorithm`	使用的优化算法
`message`	退出消息

`lambda` — 解处的拉格朗日乘数
结构体

解处的拉格朗日乘数，以包含下列字段的结构体形式返回：

`lower`	对应于 `lb` 的下界
`upper`	对应于 `ub` 的上界
`ineqlin`	对应于 `A` 和 `b` 的线性不等式
`eqlin`	对应于 `Aeq` 和 `beq` 的线性等式
`ineqnonlin`	对应于 `nonlcon` 中 `c` 的非线性不等式
`eqnonlin`	对应于 `nonlcon` 中 `ceq` 的非线性等式

`jacobian` — 解处的雅可比矩阵
实矩阵

解处的雅可比矩阵，以实矩阵形式返回。jacobian(i,j) 是 fun(i) 关于解 x 处的 x(j) 的偏导数。

对于在解处有活动约束的问题，jacobian 不适用于估计置信区间。

限制

信赖域反射算法不能求解欠定方程组；它要求方程个数（即 F 的行维度）至少与变量个数一样。在欠定的情况下，lsqnonlin 使用莱文贝格-马夸特算法。
lsqnonlin 可以直接求解复数值问题。请注意，约束对于复数值没有意义，因为复数不能很好地排序；询问一个复数值是大于还是小于另一个复数值没有意义。对于具有边界约束的复数问题，请将变量分成实部和虚部。不要对复数数据使用 'interior-point' 算法。请参阅对复数值数据进行模型拟合。
信赖域反射方法的预条件共轭梯度部分中使用的预条件子计算在计算预条件子之前形成 J^TJ（其中 J 是雅可比矩阵）。因此，如果 J 的一行包含许多非零值（这会导致近乎稠密的乘积 J^TJ），则可能导致大型问题的求解过程成本高昂。
如果 x 的分量没有上界（或下界），lsqnonlin 更倾向于 ub（或 lb）的对应分量设置为 inf（对于下界，则为 -inf），而不是任意但非常大的正数（对于下界，则为负数）。

您可以在 lsqnonlin、lsqcurvefit、fsolve 中使用信赖域反射算法求解中小规模问题，而无需计算 fun 中的雅可比矩阵或提供雅可比矩阵稀疏模式。（这也适用于使用 fmincon 或 fminunc 而不计算黑塞矩阵或提供黑塞矩阵稀疏模式的情况。）中小规模有多小？没有绝对的答案，因为这取决于您的计算机系统配置中的虚拟内存量。

假设您的问题有 m 个方程和 n 个未知数。如果命令 J = sparse(ones(m,n)) 导致您的计算机上出现 Out of memory 错误，则这肯定是因为问题太大。即使它没有导致错误，问题仍可能太大。只有运行它并查看 MATLAB 是否在系统可用的虚拟内存量内运行，您才能找到答案。

详细信息