Main Content

比较 lsqnonlin 和 fmincon 的约束非线性最小二乘法

打开实时脚本

此示例表明，在求解约束最小二乘问题时，lsqnonlin 通常比 fmincon 需要更少的函数计算。两个求解器都使用 fmincon 'interior-point' 算法来求解问题。然而 lsqnonlin 通常可以用更少的函数计算来求解问题。原因是 lsqnonlin 有更多信息可供使用。fmincon 最小化 ∑iFi2 给出的平方和，其中 F 是一个向量函数。相比之下，lsqnonlin 与整个向量 F 一起工作，这意味着它可以访问总和的所有分量。换句话说，fmincon 只能访问总和的值，但 lsqnonlin 可以分别访问每个分量。

本示例末尾列出的 runlsqfmincon 辅助函数创建了一系列缩放的 Rosenbrock 型问题，其中 N 的非线性约束从 1 到 50，其中问题变量的数量为 2N。有关 Rosenbrock 函数的描述，请参阅 基于问题求解有约束非线性问题：。该函数还绘制了结果，显示：

  • 迭代次数

  • 函数计数数量

  • 残差结果

该图显示了有限差分导数估计（标记为 FD）和使用自动微分计算的导数之间的差异。有关自动微分的描述，请参阅自动微分背景。

runlsqfmincon;

Figure contains an axes object. The axes object with title Iterations, xlabel N, ylabel Iterations contains 4 objects of type line. These objects represent lsqnonlin, lsqnonlin FD, fmincon, fmincon FD.

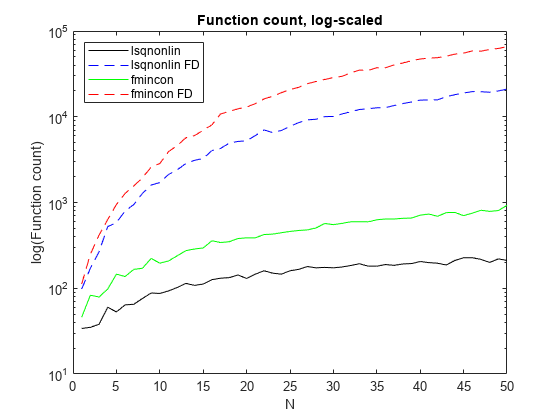
Figure contains an axes object. The axes object with title Function count, log-scaled, xlabel N, ylabel log(Function count) contains 4 objects of type line. These objects represent lsqnonlin, lsqnonlin FD, fmincon, fmincon FD.

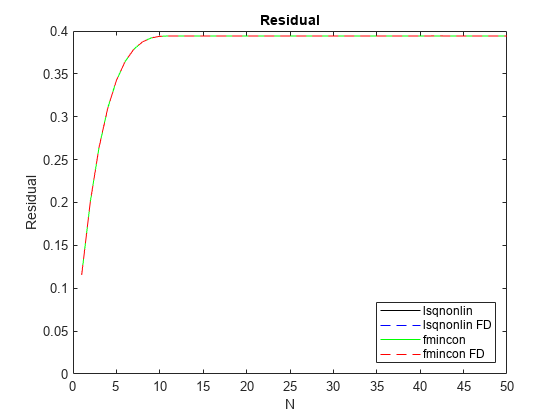
Figure contains an axes object. The axes object with title Residual, xlabel N, ylabel Residual contains 4 objects of type line. These objects represent lsqnonlin, lsqnonlin FD, fmincon, fmincon FD.

图表显示了以下典型结果。

  • 对于每个 N ， fmincon 的迭代次数是 lsqnonlin 的两倍多，并且随着 N 近似线性增加。

  • 迭代次数不依赖于导数估计方案。

  • 有限差分 (FD) 估计的函数数量比自动微分的函数数量高得多。

  • 对于相同的导数估计方案，lsqnonlin 的函数计数低于 fmincon 的函数计数。

  • 残差与所有解方法相匹配，这意味着结果与求解器和导数估计方案无关。

结果表明，无论是迭代次数还是函数计数，lsqnonlin 都比 fmincon 更高效。然而，不同的问题可能有不同的结果，并且对于某些问题， fmincon 比 lsqnonlin 更有效。

辅助函数

以下代码创建 runlsqfmincon 辅助函数。

function [lsq,lsqfd,fmin,fminfd] = runlsqfmincon()
optslsq = optimoptions("lsqnonlin",Display="none",...
    MaxFunctionEvaluations=1e5,MaxIterations=1e4); % Allow for many iterations and Fevals
optsfmincon = optimoptions("fmincon",Display="none",...
    MaxFunctionEvaluations=1e5,MaxIterations=1e4);
% Create structures to hold results
z = zeros(1,50);
lsq = struct('Iterations',z,'Fcount',z,'Residual',z);
lsqfd = lsq;
fmin = lsq;
fminfd = lsq;
rng(1) % Reproducible initial points
x00 = -1/2 + randn(50,1);
y00 = 1/2 + randn(50,1);
for N = 1:50
    x = optimvar("x",N,LowerBound=-3,UpperBound=3);
    y = optimvar("y",N,LowerBound=0,UpperBound=9);
    prob = optimproblem("Objective",sum((10*(y - x.^2)).^2 + (1 - x).^2));
    x0.x = x00(1:N);
    x0.y = y00(1:N);
    % Include a set of nonlinear inequality constraints
    cons = optimconstr(N);
    for i = 1:N
        cons(i) = x(i)^2 + y(i)^2 <= 1/2 + 1/8*i;
    end
    prob.Constraints = cons;
    [sol,fval,exitflag,output] = solve(prob,x0,Options=optslsq);
    lsq.Iterations(N) = output.iterations;
    lsq.Fcount(N) = output.funcCount;
    lsq.Residual(N) = fval;

    [sol,fval,exitflag,output] = solve(prob,x0,Options=optslsq,...
        ObjectiveDerivative='finite-differences',ConstraintDerivative='finite-differences');
    lsqfd.Iterations(N) = output.iterations;
    lsqfd.Fcount(N) = output.funcCount;
    lsqfd.Residual(N) = fval;

    [sol,fval,exitflag,output] = solve(prob,x0,Options=optsfmincon,Solver="fmincon");
    fmin.Iterations(N) = output.iterations;
    fmin.Fcount(N) = output.funcCount;
    fmin.Residual(N) = fval;

    [sol,fval,exitflag,output] = solve(prob,x0,Options=optsfmincon,Solver="fmincon",...
        ObjectiveDerivative='finite-differences',ConstraintDerivative='finite-differences');
    fminfd.Iterations(N) = output.iterations;
    fminfd.Fcount(N) = output.funcCount;
    fminfd.Residual(N) = fval;
end

N = 1:50;    
plot(N,lsq.Iterations,'k',N,lsqfd.Iterations,'b--',N,fmin.Iterations,'g',N,fminfd.Iterations,'r--')
legend('lsqnonlin','lsqnonlin FD','fmincon','fmincon FD','Location','northwest')
xlabel('N')
ylabel('Iterations')
title('Iterations')

figure
semilogy(N,lsq.Fcount,'k',N,lsqfd.Fcount,'b--',N,fmin.Fcount,'g',N,fminfd.Fcount,'r--')
legend('lsqnonlin','lsqnonlin FD','fmincon','fmincon FD','Location','northwest')
xlabel('N')
ylabel('log(Function count)')
title('Function count, log-scaled')

figure
plot(N,lsq.Residual,'k',N,lsqfd.Residual,'b--',N,fmin.Residual,'g',N,fminfd.Residual,'r--')
legend('lsqnonlin','lsqnonlin FD','fmincon','fmincon FD','Location','southeast')
xlabel('N')
ylabel('Residual')
ylim([0,0.4])
title('Residual')

end

另请参阅

| |

相关主题