solve

x = optimvar('x');
y = optimvar('y');
prob = optimproblem;
prob.Objective = -x - y/3;
prob.Constraints.cons1 = x + y <= 2;
prob.Constraints.cons2 = x + y/4 <= 1;
prob.Constraints.cons3 = x - y <= 2;
prob.Constraints.cons4 = x/4 + y >= -1;
prob.Constraints.cons5 = x + y >= 1;
prob.Constraints.cons6 = -x + y <= 2;

sol = solve(prob)

Solving problem using linprog.

Optimal solution found.

sol = struct with fields:
    x: 0.6667
    y: 1.3333

使用基于问题的方法求解非线性规划问题

打开实时脚本

在 $x^{2} + y^{2} \leq 4$ 区域内，求在 MATLAB® 中包含的 peaks 函数的最小值。为此，我们需要创建优化变量 x 和 y。

x = optimvar('x');
y = optimvar('y');

以 peaks 作为目标函数，创建一个优化问题。

prob = optimproblem("Objective",peaks(x,y));

将约束作为不等式包含在优化变量中。

prob.Constraints = x^2 + y^2 <= 4;

将 x 的初始点设置为 1，将 y 设置为 –1，并求解问题。

x0.x = 1;
x0.y = -1;
sol = solve(prob,x0)

Solving problem using fmincon.

Local minimum found that satisfies the constraints.

Optimization completed because the objective function is non-decreasing in 
feasible directions, to within the value of the optimality tolerance,
and constraints are satisfied to within the value of the constraint tolerance.

sol = struct with fields:
    x: 0.2283
    y: -1.6255

不受支持的函数要求 fcn2optimexpr

如果目标函数或非线性约束函数不完全由初等函数组成，则必须使用 fcn2optimexpr 将这些函数转换为优化表达式。请参阅将非线性函数转换为优化表达式和Supported Operations for Optimization Variables and Expressions。

按如下所示转换当前示例：

convpeaks = fcn2optimexpr(@peaks,x,y);
prob.Objective = convpeaks;
sol2 = solve(prob,x0)

Solving problem using fmincon.

Local minimum found that satisfies the constraints.

Optimization completed because the objective function is non-decreasing in 
feasible directions, to within the value of the optimality tolerance,
and constraints are satisfied to within the value of the constraint tolerance.

sol2 = struct with fields:
    x: 0.2283
    y: -1.6255

从初始点开始求解混合整数线性规划

打开实时脚本

比较在具有和没有初始可行点的情况下求解整数规划问题的步数。该问题有八个整数变量和四个线性等式约束，所有变量都限制为正值。

prob = optimproblem;
x = optimvar('x',8,1,'LowerBound',0,'Type','integer');

创建四个线性等式约束，并将它们加入问题中。

Aeq = [22    13    26    33    21     3    14    26
    39    16    22    28    26    30    23    24
    18    14    29    27    30    38    26    26
    41    26    28    36    18    38    16    26];
beq = [ 7872
       10466
       11322
       12058];
cons = Aeq*x == beq;
prob.Constraints.cons = cons;

创建目标函数，并将其加入问题中。

f = [2    10    13    17     7     5     7     3];
prob.Objective = f*x;

在不使用初始点的情况下求解问题，并检查显示以查看分支定界节点的数量。

[x1,fval1,exitflag1,output1] = solve(prob);

Solving problem using intlinprog.
LP:                Optimal objective value is 1554.047531.                                          

Cut Generation:    Applied 8 strong CG cuts.                                                        
                   Lower bound is 1591.000000.                                                      

Branch and Bound:

   nodes     total   num int        integer       relative                                          
explored  time (s)  solution           fval        gap (%)                                         
   10000      0.62         0              -              -                                          
   14739      0.84         1   2.154000e+03   2.593968e+01                                          
   18258      1.05         2   1.854000e+03   1.180593e+01                                          
   18673      1.08         2   1.854000e+03   1.563342e+00                                          
   18829      1.09         2   1.854000e+03   0.000000e+00                                          

Optimal solution found.

Intlinprog stopped because the objective value is within a gap tolerance of the optimal value, options.AbsoluteGapTolerance = 0. The intcon variables are integer within tolerance, options.IntegerTolerance = 1e-05.

为了进行比较，使用初始可行点求得解。

x0.x = [8 62 23 103 53 84 46 34]';
[x2,fval2,exitflag2,output2] = solve(prob,x0);

Solving problem using intlinprog.
LP:                Optimal objective value is 1554.047531.                                          

Cut Generation:    Applied 8 strong CG cuts.                                                        
                   Lower bound is 1591.000000.                                                      
                   Relative gap is 59.20%.                                                         

Branch and Bound:

   nodes     total   num int        integer       relative                                          
explored  time (s)  solution           fval        gap (%)                                         
    3627      0.32         2   2.154000e+03   2.593968e+01                                          
    5844      0.45         3   1.854000e+03   1.180593e+01                                          
    6204      0.47         3   1.854000e+03   1.455526e+00                                          
    6400      0.49         3   1.854000e+03   0.000000e+00                                          

Optimal solution found.

Intlinprog stopped because the objective value is within a gap tolerance of the optimal value, options.AbsoluteGapTolerance = 0. The intcon variables are integer within tolerance, options.IntegerTolerance = 1e-05.

fprintf('Without an initial point, solve took %d steps.\nWith an initial point, solve took %d steps.',output1.numnodes,output2.numnodes)

Without an initial point, solve took 18829 steps.
With an initial point, solve took 6400 steps.

给出初始点并不能始终改进问题。对于此问题，使用初始点可以节省时间和计算步数。但是，对于某些问题，初始点可能会导致 solve 采用更多步数。

基于问题指定 `surrogateopt` 的起点和值

此示例使用:

Global Optimization Toolbox Global Optimization Toolbox

打开实时脚本

对于某些求解器，您可以将目标函数和约束函数值（如果有）传递给 solve 中的 x0 参数。这可以节省求解器的时间。传递 OptimizationValues 对象的向量。使用 optimvalues 函数创建此向量。

可以使用目标函数值的求解器有：

ga
gamultiobj
paretosearch
surrogateopt

可以使用非线性约束函数值的求解器有：

paretosearch
surrogateopt

例如，使用 surrogateopt 从初始点网格中的值开始，最小化 peaks 函数。使用 x 变量创建一个从 -10 到 10 的网格，使用 y 变量创建一个从 –5/2 到 5/2 的网格，间距为 1/2。计算在初始点的目标函数值。

x = optimvar("x",LowerBound=-10,UpperBound=10);
y = optimvar("y",LowerBound=-5/2,UpperBound=5/2);
prob = optimproblem("Objective",peaks(x,y));
xval = -10:10;
yval = (-5:5)/2;
[x0x,x0y] = meshgrid(xval,yval);
peaksvals = peaks(x0x,x0y);

使用 optimvalues 传递 x0 参数中的值。这可以为 solve 节省时间，因为 solve 不需要计算这些值。将这些值作为行向量传递。

x0 = optimvalues(prob,'x',x0x(:)','y',x0y(:)',...
    "Objective",peaksvals(:)');

使用 surrogateopt 和初始值求解问题。

[sol,fval,eflag,output] = solve(prob,x0,Solver="surrogateopt")

Solving problem using surrogateopt.

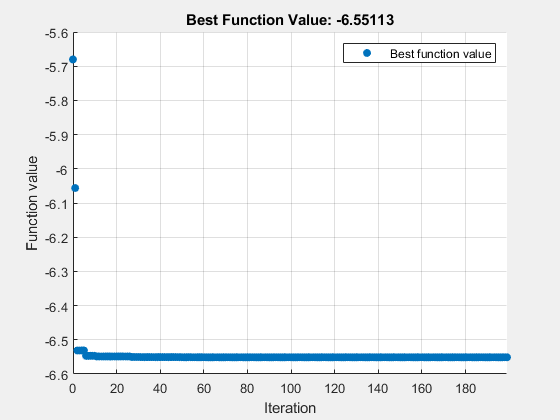
Figure Optimization Plot Function contains an axes object. The axes object with title Best Function Value: -6.55113, xlabel Iteration, ylabel Function value contains an object of type scatter. This object represents Best function value.

surrogateopt stopped because it exceeded the function evaluation limit set by 
'options.MaxFunctionEvaluations'.

sol = struct with fields:
    x: 0.2283
    y: -1.6256

fval = -6.5511

eflag = 
    SolverLimitExceeded

output = struct with fields:
        elapsedtime: 53.7052
          funccount: 200
    constrviolation: 0
               ineq: [1x1 struct]
           rngstate: [1x1 struct]
            message: 'surrogateopt stopped because it exceeded the function evaluation limit set by ...'
             solver: 'surrogateopt'

基于问题使用多起点求解器最小化非线性函数

此示例使用:

Global Optimization Toolbox Global Optimization Toolbox

打开实时脚本

从点 [–1,2] 开始，在范围 $- 5 \leq x, y \leq 5$ 上求 peaks 函数的局部最小值。

x = optimvar("x",LowerBound=-5,UpperBound=5);
y = optimvar("y",LowerBound=-5,UpperBound=5);
x0.x = -1;
x0.y = 2;
prob = optimproblem(Objective=peaks(x,y));
opts = optimoptions("fmincon",Display="none");
[sol,fval] = solve(prob,x0,Options=opts)

sol = struct with fields:
    x: -3.3867
    y: 3.6341

fval = 1.1224e-07

尝试使用 GlobalSearch 求解器求得更好的解。此求解器多次运行 fmincon，可能会产生更好的解。

ms = GlobalSearch;
[sol2,fval2] = solve(prob,x0,ms)

Solving problem using GlobalSearch.

GlobalSearch stopped because it analyzed all the trial points.

All 15 local solver runs converged with a positive local solver exit flag.

sol2 = struct with fields:
    x: 0.2283
    y: -1.6255

fval2 = -6.5511

GlobalSearch 找到一个目标函数值更好（更低）的解。退出消息显示局部求解器 fmincon 运行了 15 次。返回的解的目标函数值约为 –6.5511，低于第一个解的值 1.1224e–07。

使用非默认选项求解整数规划问题

打开实时脚本

求解问题

$\min_{x} (- 3 x_{1} - 2 x_{2} - x_{3}) s u b j e c t t o {\begin{array}{llllllllllllllllllll} x_{3} b i n a r y \\ x_{1}, x_{2} \geq 0 \\ x_{1} + x_{2} + x_{3} \leq 7 \\ 4 x_{1} + 2 x_{2} + x_{3} = 12 \end{array}$

而不显示迭代输出。

x = optimvar('x',2,1,'LowerBound',0);
x3 = optimvar('x3','Type','integer','LowerBound',0,'UpperBound',1);
prob = optimproblem;
prob.Objective = -3*x(1) - 2*x(2) - x3;
prob.Constraints.cons1 = x(1) + x(2) + x3 <= 7;
prob.Constraints.cons2 = 4*x(1) + 2*x(2) + x3 == 12;

options = optimoptions('intlinprog','Display','off');

sol = solve(prob,'Options',options)

sol = struct with fields:
     x: [2x1 double]
    x3: 1

检查解。

sol.x

sol.x3

ans = 1

使用 `intlinprog` 求解线性规划

打开实时脚本

强制 solve 使用 intlinprog 作为线性规划问题的求解器。

x = optimvar('x');
y = optimvar('y');
prob = optimproblem;
prob.Objective = -x - y/3;
prob.Constraints.cons1 = x + y <= 2;
prob.Constraints.cons2 = x + y/4 <= 1;
prob.Constraints.cons3 = x - y <= 2;
prob.Constraints.cons4 = x/4 + y >= -1;
prob.Constraints.cons5 = x + y >= 1;
prob.Constraints.cons6 = -x + y <= 2;

sol = solve(prob,'Solver', 'intlinprog')

Solving problem using intlinprog.
LP:                Optimal objective value is -1.111111.                                            


Optimal solution found.

No integer variables specified. Intlinprog solved the linear problem.

sol = struct with fields:
    x: 0.6667
    y: 1.3333

返回所有输出

打开实时脚本

求解使用非默认选项求解整数规划问题中所述的混合整数线性规划问题，并检查所有输出数据。

x = optimvar('x',2,1,'LowerBound',0);
x3 = optimvar('x3','Type','integer','LowerBound',0,'UpperBound',1);
prob = optimproblem;
prob.Objective = -3*x(1) - 2*x(2) - x3;
prob.Constraints.cons1 = x(1) + x(2) + x3 <= 7;
prob.Constraints.cons2 = 4*x(1) + 2*x(2) + x3 == 12;

[sol,fval,exitflag,output] = solve(prob)

Solving problem using intlinprog.
LP:                Optimal objective value is -12.000000.                                           


Optimal solution found.

Intlinprog stopped at the root node because the objective value is within a gap tolerance of the optimal value, options.AbsoluteGapTolerance = 0. The intcon variables are integer within tolerance, options.IntegerTolerance = 1e-05.

sol = struct with fields:
     x: [2x1 double]
    x3: 1

fval = -12

exitflag = 
    OptimalSolution

output = struct with fields:
        relativegap: 0
        absolutegap: 0
      numfeaspoints: 1
           numnodes: 0
    constrviolation: 0
            message: 'Optimal solution found....'
             solver: 'intlinprog'

对于没有任何整数约束的问题，您也可以使用第五个输出返回非空拉格朗日乘数结构体。

用索引变量查看解

打开实时脚本

使用指定的索引变量创建和求解优化问题。问题描述：将水果运往多个机场，使利润加权运量最大化，同时确保加权运量满足约束。

rng(0) % For reproducibility
p = optimproblem('ObjectiveSense', 'maximize');
flow = optimvar('flow', ...
    {'apples', 'oranges', 'bananas', 'berries'}, {'NYC', 'BOS', 'LAX'}, ...
    'LowerBound',0,'Type','integer');
p.Objective = sum(sum(rand(4,3).*flow));
p.Constraints.NYC = rand(1,4)*flow(:,'NYC') <= 10;
p.Constraints.BOS = rand(1,4)*flow(:,'BOS') <= 12;
p.Constraints.LAX = rand(1,4)*flow(:,'LAX') <= 35;
sol = solve(p);

Solving problem using intlinprog.
LP:                Optimal objective value is 1027.472366.                                          

Heuristics:        Found 1 solution using ZI round.                                                 
                   Lower bound is 1027.233133.                                                      
                   Relative gap is 0.00%.                                                          


Optimal solution found.

Intlinprog stopped at the root node because the objective value is within a gap tolerance of the optimal value, options.AbsoluteGapTolerance = 0. The intcon variables are integer within tolerance, options.IntegerTolerance = 1e-05.

找出运送至纽约和洛杉矶的橙子和浆果的最佳运量。

[idxFruit,idxAirports] = findindex(flow, {'oranges','berries'}, {'NYC', 'LAX'})

idxFruit = 1×2

     2     4

idxAirports = 1×2

     1     3

orangeBerries = sol.flow(idxFruit, idxAirports)

orangeBerries = 2×2

     0   980
    70     0

此结果表示不向 NYC 运送橙子，只将 70 份浆果运至 NYC，同时将 980 份橙子运至 LAX，而不向 LAX 运送浆果。

列出以下最佳运量：

Fruit Airports

----- --------

Berries NYC

Apples BOS

Oranges LAX

idx = findindex(flow, {'berries', 'apples', 'oranges'}, {'NYC', 'BOS', 'LAX'})

idx = 1×3

     4     5    10

optimalFlow = sol.flow(idx)

optimalFlow = 1×3

    70    28   980

此结果表示将 70 份浆果运送至 NYC，将 28 份苹果运送至 BOS，将 980 份橙子运送至 LAX。

基于问题求解非线性方程组

打开实时脚本

要使用基于问题的方法求解非线性方程组

$\begin{array}{l} \exp (- \exp (- (x_{1} + x_{2}))) = x_{2} (1 + x_{1}^{2}) \\ x_{1} \cos (x_{2}) + x_{2} \sin (x_{1}) = \frac{1}{2} \end{array}$

请首先将 x 定义为一个二元素优化变量。

x = optimvar('x',2);

创建第一个方程作为优化等式表达式。

eq1 = exp(-exp(-(x(1) + x(2)))) == x(2)*(1 + x(1)^2);

同样，创建第二个方程作为优化等式表达式。

eq2 = x(1)*cos(x(2)) + x(2)*sin(x(1)) == 1/2;

创建一个方程问题，并将这些方程放入该问题中。

prob = eqnproblem;
prob.Equations.eq1 = eq1;
prob.Equations.eq2 = eq2;

检查此问题。

show(prob)

  EquationProblem : 

	Solve for:
       x


 eq1:
       exp((-exp((-(x(1) + x(2)))))) == (x(2) .* (1 + x(1).^2))

 eq2:
       ((x(1) .* cos(x(2))) + (x(2) .* sin(x(1)))) == 0.5

从 [0,0] 点开始求解问题。对于基于问题的方法，将初始点指定为结构体，并将变量名称作为结构体的字段。对于此问题，只有一个变量，即 x。

x0.x = [0 0];
[sol,fval,exitflag] = solve(prob,x0)

Solving problem using fsolve.

Equation solved.

fsolve completed because the vector of function values is near zero
as measured by the value of the function tolerance, and
the problem appears regular as measured by the gradient.

sol = struct with fields:
    x: [2x1 double]

fval = struct with fields:
    eq1: -2.4070e-07
    eq2: -3.8255e-08

exitflag = 
    EquationSolved

查看解点。

disp(sol.x)

    0.3532
    0.6061

不受支持的函数要求 fcn2optimexpr

如果方程函数不是由初等函数组成的，您必须使用 fcn2optimexpr 将函数转换为优化表达式。对于本示例：

ls1 = fcn2optimexpr(@(x)exp(-exp(-(x(1)+x(2)))),x);
eq1 = ls1 == x(2)*(1 + x(1)^2);
ls2 = fcn2optimexpr(@(x)x(1)*cos(x(2))+x(2)*sin(x(1)),x);
eq2 = ls2 == 1/2;

请参阅Supported Operations for Optimization Variables and Expressions和将非线性函数转换为优化表达式。

输入参数

全部折叠

`prob` — 优化问题或方程问题
`OptimizationProblem` 对象 | `EquationProblem` 对象

优化问题或方程问题，指定为 OptimizationProblem 对象或 EquationProblem 对象。使用 optimproblem 创建优化问题；使用 eqnproblem 创建方程问题。

警告

基于问题的方法不支持目标函数、非线性等式或非线性不等式中使用复数值。如果某函数计算具有复数值，即使是作为中间值，最终结果也可能不正确。

示例: prob = optimproblem; prob.Objective = obj; prob.Constraints.cons1 = cons1;

示例: prob = eqnproblem; prob.Equations = eqs;

`x0` — 初始点
结构体 | `OptimizationValues` 对象的向量

初始点，指定为结构体，其字段名称等于 prob 中的变量名称。

对于某些 Global Optimization Toolbox 求解器，x0 可以是表示多个初始点的 OptimizationValues 对象的向量。使用 optimvalues 函数创建这些点。这些求解器包括：

ga (Global Optimization Toolbox)、gamultiobj (Global Optimization Toolbox)、paretosearch (Global Optimization Toolbox) 和 particleswarm (Global Optimization Toolbox)。这些求解器接受多个起点作为初始种群的成员。
MultiStart (Global Optimization Toolbox).此求解器可对局部求解器（如 fmincon）应用多个初始点。
surrogateopt (Global Optimization Toolbox).此求解器接受多个初始点，以帮助创建一个初始替代。

有关以命名索引变量指定 x0 的示例，请参阅Create Initial Point for Optimization with Named Index Variables。

示例: 如果 prob 具有名为 x 和 y 的变量：x0.x = [3,2,17]; x0.y = [pi/3,2*pi/3]。

数据类型: struct

`ms` — 多起点求解器
`MultiStart` 对象 | `GlobalSearch` 对象

多起点求解器，指定为 MultiStart (Global Optimization Toolbox) 对象或 GlobalSearch (Global Optimization Toolbox) 对象。使用 MultiStart 或 GlobalSearch 命令创建 ms。

当前，GlobalSearch 仅支持 fmincon 局部求解器；MultiStart 仅支持 fmincon、fminunc 和 lsqnonlin 局部求解器。

示例: ms = MultiStart;

示例: ms = GlobalSearch(FunctionTolerance=1e-4);

名称-值参数

将可选的参数对组指定为 Name1=Value1,...,NameN=ValueN，其中 Name 是参数名称，Value 是对应的值。名称-值参数必须出现在其他参数之后，但参数对组的顺序无关紧要。

在 R2021a 之前，使用逗号分隔每个名称和值，并用引号将 Name 引起来。

示例: solve(prob,'Options',opts)

`MinNumStartPoints` — `MultiStart` 的最小起点数
20 (默认) | 正整数

MultiStart (Global Optimization Toolbox) 的最小起点数，指定为正整数。仅当使用 ms 参数调用 solve 时，此参数才适用。solve 使用 x0 中的所有值作为起点。如果 MinNumStartPoints 大于 x0 中的值的数目，则 solve 会在问题边界内均匀且随机地生成更多起点。如果某个分量为无界，solve 使用 MultiStart 的默认人为边界生成这些点。

示例: solve(prob,x0,ms,MinNumStartPoints=50)

数据类型: double

`Options` — 优化选项
由 `optimoptions` 创建的对象 | options 结构体

优化选项，指定为一个由 optimoptions 创建的对象，或一个由 optimset 等创建的 options 结构体。

在内部，solve 函数调用相关求解器，详见 'solver' 参数参考。确保 options 与求解器兼容。例如，intlinprog 不允许选项为结构体，lsqnonneg 不允许选项为对象。

有关改进 intlinprog 解或求解速度的选项设置的建议，请参阅Tuning Integer Linear Programming。对于 linprog，默认的 'dual-simplex' 算法通常内存利用的效率高且速度快。偶尔，当 Algorithm 选项为 'interior-point' 时，linprog 求解大型问题更快。有关改进非线性问题的解的选项设置的建议，请参阅Optimization Options in Common Use: Tuning and Troubleshooting和改进结果。

示例: options = optimoptions('intlinprog','Display','none')

`Solver` — 优化求解器
`'intlinprog'` | `'linprog'` | `'lsqlin'` | `'lsqcurvefit'` | `'lsqnonlin'` | `'lsqnonneg'` | `'quadprog'` | `'fminbnd'` | `'fminunc'` | `'fmincon'` | `'fminsearch'` | `'fzero'` | `'fsolve'` | `'coneprog'` | `'ga'` | `'gamultiobj'` | `'paretosearch'` | `'patternsearch'` | `'particleswarm'` | `'surrogateopt'` | `'simulannealbnd'`

优化求解器，指定为一个列出的求解器的名称。对于优化问题，下表包含每个问题类型的可用求解器，包括来自 Global Optimization Toolbox 的求解器。方程问题的详细信息显示在优化求解器详细信息下方。

对于使用 prob2struct 转换具有整数约束的非线性问题，生成的问题结构体可能取决于所选求解器。如果您没有 Global Optimization Toolbox 许可证，则必须指定求解器。请参阅基于问题的非线性优化中的整数约束。

此处列出了每种优化问题类型的默认求解器。

问题类型	默认求解器
线性规划 (LP)	`linprog`
混合整数线性规划 (MILP)	`intlinprog`
二次规划 (QP)	`quadprog`
二阶锥规划 (SOCP)	`coneprog`
线性最小二乘	`lsqlin`
非线性最小二乘	`lsqnonlin`
非线性规划 (NLP)	`fminunc` 用于没有约束的问题，否则使用 `fmincon`
混合整数非线性规划 (MINLP)	`ga` (Global Optimization Toolbox)
多目标	`gamultiobj` (Global Optimization Toolbox)

在下表中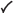， Yes 表示对应求解器可用于该问题类型，x 表示对应求解器不可用。

问题类型	LP	MILP	QP	SOCP	线性最小二乘	非线性最小二乘	NLP	MINLP
求解器
`linprog`		x	x	x	x	x	x	x
`intlinprog`			x	x	x	x	x	x
`quadprog`		x				x	x	x
`coneprog`		x	x		x	x	x	x
`lsqlin`	x	x	x	x		x	x	x
`lsqnonneg`	x	x	x	x		x	x	x
`lsqnonlin`	x	x	x	x			x	x
`fminunc`		x		x				x
`fmincon`		x						x
`fminbnd`	x	x	x	x				x
`fminsearch`	x	x	x	x				x
`patternsearch` (Global Optimization Toolbox)		x						x
`ga` (Global Optimization Toolbox)
`particleswarm` (Global Optimization Toolbox)		x		x				x
`simulannealbnd` (Global Optimization Toolbox)		x		x				x
`surrogateopt` (Global Optimization Toolbox)
`gamultiobj` (Global Optimization Toolbox)
`paretosearch` (Global Optimization Toolbox)		x						x

注意

如果您选择 lsqcurvefit 作为最小二乘问题的求解器，solve 将使用 lsqnonlin。对于 solve，lsqcurvefit 和 lsqnonlin 求解器是相同的。

小心

对于最大化问题（prob.ObjectiveSense 为 "max" 或 "maximize"），不要指定最小二乘求解器（名称以 lsq 开头的求解器）。如果指定，则 solve 会引发错误，因为这些求解器无法最大化。

对于方程求解，下表包含每个问题类型的可用求解器。在表中，

* 表示该问题类型的默认求解器。
Y 表示可用的求解器。
N 表示不可用的求解器。

方程支持的求解器

方程类型	`lsqlin`	`lsqnonneg`	`fzero`	`fsolve`	`lsqnonlin`
线性	*	N	Y（仅标量）	Y	Y
线性加边界	*	Y	N	N	Y
标量非线性	N	N	*	Y	Y
非线性方程组	N	N	N	*	Y
非线性方程组加边界	N	N	N	N	*

示例: 'intlinprog'

数据类型: char | string

`ObjectiveDerivative` — 对目标函数使用自动微分的指示
`'auto'` (默认) | `'auto-forward'` | `'auto-reverse'` | `'finite-differences'`

指示对非线性目标函数使用自动微分 (AD)，指定为 'auto'（如果可能，请使用 AD）、'auto-forward'（如果可能，请使用正向 AD）、'auto-reverse'（如果可能，请使用反向 AD）或 'finite-differences'（请不要使用 AD）。包括 auto 在内的选择项会使基础求解器在求解问题时使用梯度信息，前提是目标函数受支持，如Supported Operations for Optimization Variables and Expressions中所述。有关示例，请参阅Effect of Automatic Differentiation in Problem-Based Optimization。

默认情况下，求解器选择以下 AD 类型：

对于一般的非线性目标函数，fmincon 默认选择反向 AD。对于非线性约束函数，如果其非线性约束的数量小于变量数目，fmincon 默认选择反向 AD。否则，fmincon 默认选择正向 AD。
对于一般的非线性目标函数，fminunc 默认选择反向 AD。
对于最小二乘目标函数，fmincon 和 fminunc 对目标函数默认选择正向 AD。有关基于问题的最小二乘目标函数的定义，请参阅Write Objective Function for Problem-Based Least Squares。
当目标向量中的元素数大于或等于变量数时，lsqnonlin 默认选择正向 AD。否则，lsqnonlin 默认选择反向 AD。
当方程数大于或等于变量数时，fsolve 默认选择正向 AD。否则，fsolve 默认选择反向 AD。

示例: 'finite-differences'

数据类型: char | string

`ConstraintDerivative` — 对约束函数使用自动微分的指示
`'auto'` (默认) | `'auto-forward'` | `'auto-reverse'` | `'finite-differences'`

指示对非线性约束函数使用自动微分 (AD)，指定为 'auto'（如果可能，请使用 AD）、'auto-forward'（如果可能，请使用正向 AD）、'auto-reverse'（如果可能，请使用反向 AD）或 'finite-differences'（请不要使用 AD）。包括 auto 在内的选择项会使基础求解器在求解问题时使用梯度信息，前提是约束函数受支持，如Supported Operations for Optimization Variables and Expressions中所述。有关示例，请参阅Effect of Automatic Differentiation in Problem-Based Optimization。

默认情况下，求解器选择以下 AD 类型：

对于一般的非线性目标函数，fmincon 默认选择反向 AD。对于非线性约束函数，如果其非线性约束的数量小于变量数目，fmincon 默认选择反向 AD。否则，fmincon 默认选择正向 AD。
对于一般的非线性目标函数，fminunc 默认选择反向 AD。
对于最小二乘目标函数，fmincon 和 fminunc 对目标函数默认选择正向 AD。有关基于问题的最小二乘目标函数的定义，请参阅Write Objective Function for Problem-Based Least Squares。
当目标向量中的元素数大于或等于变量数时，lsqnonlin 默认选择正向 AD。否则，lsqnonlin 默认选择反向 AD。
当方程数大于或等于变量数时，fsolve 默认选择正向 AD。否则，fsolve 默认选择反向 AD。

示例: 'finite-differences'

数据类型: char | string

`EquationDerivative` — 对方程使用自动微分的指示
`'auto'` (默认) | `'auto-forward'` | `'auto-reverse'` | `'finite-differences'`

指示对非线性约束函数使用自动微分 (AD)，指定为 'auto'（如果可能，请使用 AD）、'auto-forward'（如果可能，请使用正向 AD）、'auto-reverse'（如果可能，请使用反向 AD）或 'finite-differences'（请不要使用 AD）。包括 auto 在内的选择项会使基础求解器在求解问题时使用梯度信息，前提是方程函数受支持，如Supported Operations for Optimization Variables and Expressions中所述。有关示例，请参阅Effect of Automatic Differentiation in Problem-Based Optimization。

默认情况下，求解器选择以下 AD 类型：

对于一般的非线性目标函数，fmincon 默认选择反向 AD。对于非线性约束函数，如果其非线性约束的数量小于变量数目，fmincon 默认选择反向 AD。否则，fmincon 默认选择正向 AD。
对于一般的非线性目标函数，fminunc 默认选择反向 AD。
对于最小二乘目标函数，fmincon 和 fminunc 对目标函数默认选择正向 AD。有关基于问题的最小二乘目标函数的定义，请参阅Write Objective Function for Problem-Based Least Squares。
当目标向量中的元素数大于或等于变量数时，lsqnonlin 默认选择正向 AD。否则，lsqnonlin 默认选择反向 AD。
当方程数大于或等于变量数时，fsolve 默认选择正向 AD。否则，fsolve 默认选择反向 AD。

示例: 'finite-differences'

数据类型: char | string

输出参数

全部折叠

`sol` — 解
结构体 | `OptimizationValues` 向量

解，以结构体或 OptimizationValues 向量形式返回。对于多目标问题，sol 是 OptimizationValues 向量。对于单目标问题，返回的结构体的字段是问题中优化变量的名称。请参阅 optimvar。

`fval` — 解处的目标函数值
实数 | 实数向量 | 实矩阵 | 结构体

在解处的目标函数值，返回为下列值之一：

问题类型	返回的值
优化标量目标函数 f(x)	实数 f(sol)
最小二乘	实数，在解处的残差平方和
求解方程	如果 `prob.Equations` 是单一条目：在解处的函数值实数向量，即方程的左侧减去右侧
求解方程	如果 `prob.Equations` 有多个命名字段：与 `prob.Equations` 同名的结构体，其中每个字段值都是命名方程的左侧减去右侧
多目标	矩阵，其中每个目标函数分量对应一行，每个解点对应一列。

提示

如果您忘记对定义为优化表达式或方程表达式的目标求 fval，您可以使用以下公式进行计算

fval = evaluate(prob.Objective,sol)

如果目标定义为只包含一个字段的结构体，则使用

fval = evaluate(prob.Objective.ObjectiveName,sol)

如果目标是包含多个字段的结构体，则请编写一个循环。

fnames = fields(prob.Equations);
for i = 1:length(fnames)
    fval.(fnames{i}) = evaluate(prob.Equations.(fnames{i}),sol);
end

`exitflag` — 求解器停止的原因
枚举变量

求解器停止的原因，以枚举变量形式返回。您可以使用 double(exitflag) 将 exitflag 转换为其等效数值，使用 string(exitflag) 将其转换为其等效字符串。

下表说明了 intlinprog 求解器的退出标志。

`intlinprog` 的退出标志	等效数值	含义
`OptimalWithPoorFeasibility`	`3`	解关于相对 `ConstraintTolerance` 容差可行，但关于绝对容差不可行。
`IntegerFeasible`	2	`intlinprog` 过早停止，并找到一个整数可行点。
`OptimalSolution`	`1`	求解器收敛于解 `x`。
`SolverLimitExceeded`	`0`	`intlinprog` 超过以下容差之一： `LPMaxIterations` `MaxNodes` `MaxTime` `RootLPMaxIterations` 请参阅容差和停止条件。当在根节点发生内存不足时，`solve` 也会返回此退出标志。
`OutputFcnStop`	`-1`	`intlinprog` 由输出函数或绘图函数停止。
`NoFeasiblePointFound`	`-2`	找不到可行点。
`Unbounded`	`-3`	此问题无界。
`FeasibilityLost`	`-9`	求解器失去可行性。

退出标志 3 和 -9 与不可行性较大的解相关。此类问题通常源于具有较大条件数的线性约束矩阵，或源于具有较大解分量的问题。要纠正这些问题，请尝试缩放系数矩阵，消除冗余线性约束，或对变量给出更严格的边界。

下表说明了 linprog 求解器的退出标志。

`linprog` 的退出标志	等效数值	含义
`OptimalWithPoorFeasibility`	`3`	解关于相对 `ConstraintTolerance` 容差可行，但关于绝对容差不可行。
`OptimalSolution`	`1`	求解器收敛于解 `x`。
`SolverLimitExceeded`	`0`	迭代次数超出 `options.MaxIterations`。
`NoFeasiblePointFound`	`-2`	找不到可行点。
`Unbounded`	`-3`	此问题无界。
`FoundNaN`	`-4`	在算法执行期间遇到 `NaN` 值。
`PrimalDualInfeasible`	`-5`	原始问题和对偶问题均不可行。
`DirectionTooSmall`	`-7`	搜索方向太小。无法取得进一步进展。
`FeasibilityLost`	`-9`	求解器失去可行性。

下表说明了 lsqlin 求解器的退出标志。

`lsqlin` 的退出标志	等效数值	含义
`FunctionChangeBelowTolerance`	`3`	残差的变化小于指定容差 `options.FunctionTolerance`。（`trust-region-reflective` 算法）
`StepSizeBelowTolerance`	`2`	步长小于 `options.StepTolerance`，满足约束。（`interior-point` 算法）
`OptimalSolution`	`1`	求解器收敛于解 `x`。
`SolverLimitExceeded`	`0`	迭代次数超出 `options.MaxIterations`。
`NoFeasiblePointFound`	`-2`	对于优化问题，此问题不可行。或者，对于 `interior-point` 算法，步长小于 `options.StepTolerance`，但不满足约束。对于方程问题，找不到解。
`IllConditioned`	`-4`	病态会妨碍进一步优化。
`NoDescentDirectionFound`	`-8`	搜索方向太小。无法取得进一步进展。（`interior-point` 算法）

下表说明了 quadprog 求解器的退出标志。

`quadprog` 的退出标志	等效数值	含义
`LocalMinimumFound`	`4`	找到局部最小值；最小值不唯一。
`FunctionChangeBelowTolerance`	`3`	目标函数值的变化小于指定容差 `options.FunctionTolerance`。（`trust-region-reflective` 算法）
`StepSizeBelowTolerance`	`2`	步长小于 `options.StepTolerance`，满足约束。（`interior-point-convex` 算法）
`OptimalSolution`	`1`	求解器收敛于解 `x`。
`SolverLimitExceeded`	`0`	迭代次数超出 `options.MaxIterations`。
`NoFeasiblePointFound`	`-2`	此问题不可行。或者，对于 `interior-point` 算法，步长小于 `options.StepTolerance`，但不满足约束。
`IllConditioned`	`-4`	病态会妨碍进一步优化。
`Nonconvex`	`-6`	检测到非凸问题。（`interior-point-convex` 算法）
`NoDescentDirectionFound`	`-8`	无法计算步的方向。（`interior-point-convex` 算法）

下表说明了 coneprog 求解器的退出标志。

`coneprog` 的退出标志	等效数值	含义
`OptimalSolution`	`1`	求解器收敛于解 `x`。
`SolverLimitExceeded`	`0`	迭代次数超过 `options.MaxIterations`，或以秒为单位的求解时间超过 `options.MaxTime`。
`NoFeasiblePointFound`	`-2`	此问题不可行。
`Unbounded`	`-3`	此问题无界。
`DirectionTooSmall`	`-7`	搜索方向的模变得太小。无法取得进一步进展。
`Unstable`	`-10`	此问题在数值上不稳定。

下表说明了 lsqcurvefit 或 lsqnonlin 求解器的退出标志。

`lsqnonlin` 的退出标志	等效数值	含义
`SearchDirectionTooSmall`	`4`	搜索方向的模小于 `options.StepTolerance`。
`FunctionChangeBelowTolerance`	`3`	残差的变化小于 `options.FunctionTolerance`。
`StepSizeBelowTolerance`	`2`	步长小于 `options.StepTolerance`。
`OptimalSolution`	`1`	求解器收敛于解 `x`。
`SolverLimitExceeded`	`0`	迭代次数超出 `options.MaxIterations` 或函数计算次数超过 `options.MaxFunctionEvaluations`。
`OutputFcnStop`	`-1`	由输出函数或绘图函数停止。
`NoFeasiblePointFound`	`-2`	对于优化问题，此问题不可行：边界 `lb` 和 `ub` 不一致。对于方程问题，找不到解。

下表说明了 fminunc 求解器的退出标志。

`fminunc` 的退出标志	等效数值	含义
`NoDecreaseAlongSearchDirection`	`5`	目标函数的预测下降小于 `options.FunctionTolerance` 容差。
`FunctionChangeBelowTolerance`	`3`	目标函数值的变化小于 `options.FunctionTolerance` 容差。
`StepSizeBelowTolerance`	`2`	`x` 中的变化小于 `options.StepTolerance` 容差。
`OptimalSolution`	`1`	梯度的模小于 `options.OptimalityTolerance` 容差。
`SolverLimitExceeded`	`0`	迭代次数超过 `options.MaxIterations` 或函数计算次数超过 `options.MaxFunctionEvaluations`。
`OutputFcnStop`	`-1`	由输出函数或绘图函数停止。
`Unbounded`	`-3`	当前迭代的目标函数低于 `options.ObjectiveLimit`。

下表说明了 fmincon 求解器的退出标志。

`fmincon` 的退出标志	等效数值	含义
`NoDecreaseAlongSearchDirection`	`5`	搜索方向的方向导数的模小于 2*`options.OptimalityTolerance`，最大约束违反值小于 `options.ConstraintTolerance`。
`SearchDirectionTooSmall`	`4`	搜索方向的模小于 2*`options.StepTolerance`，最大约束违反值小于 `options.ConstraintTolerance`。
`FunctionChangeBelowTolerance`	`3`	目标函数值的变化小于 `options.FunctionTolerance`，最大约束违反值小于 `options.ConstraintTolerance`。
`StepSizeBelowTolerance`	`2`	`x` 的变化小于 `options.StepTolerance`，最大约束违反值小于 `options.ConstraintTolerance`。
`OptimalSolution`	`1`	一阶最优性测度小于 `options.OptimalityTolerance`，最大约束违反值小于 `options.ConstraintTolerance`。
`SolverLimitExceeded`	`0`	迭代次数超过 `options.MaxIterations` 或函数计算次数超过 `options.MaxFunctionEvaluations`。
`OutputFcnStop`	`-1`	由输出函数或绘图函数停止。
`NoFeasiblePointFound`	`-2`	找不到可行点。
`Unbounded`	`-3`	当前迭代的目标函数低于 `options.ObjectiveLimit`，最大约束违反值小于 `options.ConstraintTolerance`。

下表说明了 fsolve 求解器的退出标志。

`fsolve` 的退出标志	等效数值	含义
`SearchDirectionTooSmall`	`4`	搜索方向的模小于 `options.StepTolerance`，方程已解。
`FunctionChangeBelowTolerance`	`3`	目标函数值的变化小于 `options.FunctionTolerance`，方程已解。
`StepSizeBelowTolerance`	`2`	`x` 中的变化小于 `options.StepTolerance`，方程已解。
`OptimalSolution`	`1`	一阶最优性测度小于 `options.OptimalityTolerance`，方程已解。
`SolverLimitExceeded`	`0`	迭代次数超过 `options.MaxIterations` 或函数计算次数超过 `options.MaxFunctionEvaluations`。
`OutputFcnStop`	`-1`	由输出函数或绘图函数停止。
`NoFeasiblePointFound`	`-2`	收敛于非根点。
`TrustRegionRadiusTooSmall`	`-3`	方程未得解。信赖域半径变得太小（`trust-region-dogleg` 算法）。

下表说明了 fzero 求解器的退出标志。

`fzero` 的退出标志	等效数值	含义
`OptimalSolution`	`1`	方程已解。
`OutputFcnStop`	`-1`	由输出函数或绘图函数停止。
`FoundNaNInfOrComplex`	`-4`	在搜索包含符号变化的区间时遇到 `NaN`、`Inf` 或复数值。
`SingularPoint`	`-5`	可能收敛于一个奇异点。
`CannotDetectSignChange`	`-6`	找不到函数值的符号相反的两个点。

下表说明了 patternsearch 求解器的退出标志。

`patternsearch` 的退出标志	等效数值	含义
`SearchDirectionTooSmall`	`4`	步长的量级小于机器精度，约束违反值小于 `ConstraintTolerance`。
`FunctionChangeBelowTolerance`	`3`	`fval` 中的变化和网格大小都小于指定的容差，并且约束违反值小于 `ConstraintTolerance`。
`StepSizeBelowTolerance`	`2`	`x` 中的变化和网格大小都小于 `StepTolerance`，并且约束违反值小于 `ConstraintTolerance`。
`SolverConvergedSuccessfully`	`1`	无非线性约束 - 网格大小的量级小于指定的容差，并且约束违反值小于 `ConstraintTolerance`。
`SolverConvergedSuccessfully`	`1`	有非线性约束 - 互补度量（在此表后定义）的量级小于 `sqrt(ConstraintTolerance)`，子问题是使用比 `MeshTolerance` 更精细的网格来求解的，并且约束违反值小于 `ConstraintTolerance`。
`SolverLimitExceeded`	`0`	达到函数计算或迭代的最大次数。
`OutputFcnStop`	`-1`	由输出函数或绘图函数停止。
`NoFeasiblePointFound`	`-2`	找不到可行点。

在非线性约束求解器中，互补测度是元素为 c_iλ_i 的向量的范数，其中 c_i 是非线性不等式约束违反值，λ_i 是对应的拉格朗日乘数。

下表说明了 ga 求解器的退出标志。

`ga` 的退出标志	等效数值	含义
`MinimumFitnessLimitReached`	`5`	达到最小适应度限值 `FitnessLimit`，约束违反值小于 `ConstraintTolerance`。
`SearchDirectionTooSmall`	`4`	步长的量级小于机器精度，约束违反值小于 `ConstraintTolerance`。
`FunctionChangeBelowTolerance`	`3`	适应度函数的值在 `MaxStallGenerations` 代中没有变化，约束违反值小于 `ConstraintTolerance`。
`SolverConvergedSuccessfully`	`1`	无非线性约束 - 适应度函数值在 `MaxStallGenerations` 代内的平均累积变化小于 `FunctionTolerance`，约束违反值小于 `ConstraintTolerance`。
`SolverConvergedSuccessfully`	`1`	有非线性约束 - 互补测度（请参阅 Complementarity Measure (Global Optimization Toolbox)）的量级小于 `sqrt(ConstraintTolerance)`，子问题是使用小于 `FunctionTolerance` 的容差求解的，约束违反值小于 `ConstraintTolerance`。
`SolverLimitExceeded`	`0`	超过最大代数 `MaxGenerations`。
`OutputFcnStop`	`-1`	由输出函数或绘图函数停止。
`NoFeasiblePointFound`	`-2`	找不到可行点。
`StallTimeLimitExceeded`	`-4`	超过停滞时间限制 `MaxStallTime`。
`TimeLimitExceeded`	`-5`	超过时间限制 `MaxTime`。

下表说明了 particleswarm 求解器的退出标志。

`particleswarm` 的退出标志	等效数值	含义
`SolverConvergedSuccessfully`	`1`	在前 `options.MaxStallIterations` 次迭代中目标值的相对变化小于 `options.FunctionTolerance`。
`SolverLimitExceeded`	`0`	迭代次数超出 `options.MaxIterations`。
`OutputFcnStop`	`-1`	迭代被输出函数或绘图函数停止。
`NoFeasiblePointFound`	`-2`	边界不一致：对于某些 `i`，`lb(i)` > `ub(i)`。
`Unbounded`	`-3`	最佳目标函数值低于 `options.ObjectiveLimit`。
`StallTimeLimitExceeded`	`-4`	最佳目标函数值在 `options.MaxStallTime` 秒内没有变化。
`TimeLimitExceeded`	`-5`	运行时间超过 `options.MaxTime` 秒。

下表说明了 simulannealbnd 求解器的退出标志。

`simulannealbnd` 的退出标志	等效数值	含义
`ObjectiveValueBelowLimit`	`5`	目标函数值小于 `options.ObjectiveLimit`。
`SolverConvergedSuccessfully`	`1`	在 `options.MaxStallIterations` 次迭代中，目标函数值的平均变化小于 `options.FunctionTolerance`。
`SolverLimitExceeded`	`0`	超过最大代数 `MaxGenerations`。
`OutputFcnStop`	`-1`	优化被输出函数或绘图函数终止。
`NoFeasiblePointFound`	`-2`	找不到可行点。
`TimeLimitExceeded`	`-5`	超过时间限制。

下表说明了 surrogateopt 求解器的退出标志。

`surrogateopt` 的退出标志	等效数值	含义
`BoundsEqual`	`10`	由于以下原因之一，问题有唯一可行的解：所有上界 `ub` (Global Optimization Toolbox) 都等于下界 `lb` (Global Optimization Toolbox)。线性等式约束 `Aeq*x = beq` 和边界有唯一解点。 `surrogateopt` 返回可行点和函数值，而不执行任何优化。
`FeasiblePointFound`	`3`	找到可行点。求解器停止，因为找到的新可行点太少，无法继续。
`ObjectiveLimitAttained`	`1`	目标函数值小于 `options.ObjectiveLimit`。当两个退出标志都适用时，此退出标志的优先级高于退出标志 `10`。
`SolverLimitExceeded`	`0`	函数计算的次数超过 `options.MaxFunctionEvaluations` 或历时超过 `options.MaxTime`。如果该问题有非线性不等式，则解可行。
`OutputFcnStop`	`-1`	优化被输出函数或绘图函数终止。
`NoFeasiblePointFound`	`-2`	由于以下原因之一，找不到可行点：下界 `lb(i)` 超过对应的上界 `ub(i)`。或者对于 `intcon` (Global Optimization Toolbox) 中 i，存在一个或多个 `ceil(lb(i))` 超过对应的 `floor(ub(i))`。在这种情况下，`solve` 返回 `x = []` 和 `fval = []`。 `lb = ub` 并且点 `lb` 不可行。在这种情况下，`x = lb` 且 `fval = objconstr(x).Fval`。线性约束和整数约束（如果存在）与边界一同存在时是不可行的。在这种情况下，`solve` 返回 `x = []` 和 `fval = []`。边界、整数和线性约束是可行的，但在非线性约束下找不到可行解。在这种情况下，`x` 是非线性约束下最小的最大不可行性点，并且 `fval = objconstr(x).Fval`。

下表说明了 MultiStart 和 GlobalSearch 求解器的退出标志。

`MultiStart` 或 `GlobalSearch` 的退出标志	等效数值	含义
`LocalMinimumFoundSomeConverged`	`2`	找到至少一个局部最小值。局部求解器的某些运行已收敛。
`LocalMinimumFoundAllConverged`	`1`	找到至少一个局部最小值。局部求解器的所有运行都已收敛。
`SolverLimitExceeded`	`0`	找不到局部最小值。至少调用了一次局部求解器，并且局部求解器调用超出迭代次数至少一次。
`OutputFcnStop`	`–1`	由输出函数或绘图函数停止。
`NoFeasibleLocalMinimumFound`	`–2`	找不到可行的局部最小值。
`TimeLimitExceeded`	`–5`	超过 `MaxTime` 限制。
`NoSolutionFound`	`–8`	找不到解。所有运行都有局部求解器退出标志 –2 或更小值，但不都等于 –2。
`FailureInSuppliedFcn`	`–10`	在目标函数或非线性约束函数中遇到失败。

下表说明了 paretosearch 求解器的退出标志。

`paretosearch` 的退出标志	等效数值	含义
`SolverConvergedSuccessfully`	`1`	满足以下条件之一：所有现任点的网格大小小于 `options.MeshTolerance`，并且约束（如果有）满足在 `options.ConstraintTolerance` 内。帕累托集的间距的相对变化小于 `options.ParetoSetChangeTolerance`，并且约束（如果有）满足在 `options.ConstraintTolerance` 内。帕累托集的体积的相对变化小于 `options.ParetoSetChangeTolerance`，并且约束（如果有）满足在 `options.ConstraintTolerance` 内。
`SolverLimitExceeded`	`0`	迭代次数超过 `options.MaxIterations` 或函数计算次数超过 `options.MaxFunctionEvaluations`。
`OutputFcnStop`	`–1`	由输出函数或绘图函数停止。
`NoFeasiblePointFound`	`–2`	求解器找不到满足所有约束的点。
`TimeLimitExceeded`	`–5`	优化时间超过 `options.MaxTime`。

下表说明了 gamultiobj 求解器的退出标志。

`paretosearch` 的退出标志	等效数值	含义
`SolverConvergedSuccessfully`	`1`	`options.MaxStallGenerations` 代内间距值相对变化的几何平均值小于 `options.FunctionTolerance`，且最终间距小于过去 `options.MaxStallGenerations` 代内的均值间距。
`SolverLimitExceeded`	`0`	代数超出 `options.MaxGenerations`。
`OutputFcnStop`	`–1`	由输出函数或绘图函数停止。
`NoFeasiblePointFound`	`–2`	求解器找不到满足所有约束的点。
`TimeLimitExceeded`	`–5`	优化时间超过 `options.MaxTime`。

`output` — 有关优化过程的信息
结构体

有关优化过程的信息，以结构体形式返回。输出结构体包含相关基础求解器输出字段中的字段，具体取决于调用了哪个求解器 solve：

'fmincon' output
'fminunc' output
'fsolve' output
'fzero' output
'intlinprog' output
'linprog' output
'lsqcurvefit' 或 'lsqnonlin' output
'lsqlin' output
'lsqnonneg' output
'quadprog' output

'ga' output (Global Optimization Toolbox)
'gamultiobj' output (Global Optimization Toolbox)
'paretosearch' output (Global Optimization Toolbox)
'particleswarm' output (Global Optimization Toolbox)
'patternsearch' output (Global Optimization Toolbox)
'simulannealbnd' output (Global Optimization Toolbox)
'surrogateopt' output (Global Optimization Toolbox)

'MultiStart' 和 'GlobalSearch' 从局部求解器返回输出结构体。此外，输出结构体包含以下字段：
- globalSolver - 'MultiStart' 或 'GlobalSearch'。
- objectiveDerivative - 采用本节末尾描述的值。
- constraintDerivative - 采用本节末尾描述的值，或当 prob 没有非线性约束时采用 "auto"。
- solver - 局部求解器，例如 'fmincon'。
- local - 包含有关优化的额外信息的结构体。
  - sol - 局部解，以 OptimizationValues 对象的向量形式返回。
  - x0 - 局部求解器的初始点，以元胞数组形式返回。
  - exitflag - 局部解的退出标志，以整数向量形式返回。
  - output - 结构体数组，每个局部解对应一行。每行是一个局部输出结构体，对应一个局部解。

solve 在 output 结构体中包含额外字段 Solver，用于标识所使用的求解器，例如 'intlinprog'。

当 Solver 是非线性 Optimization Toolbox™ 求解器时，solve 包含一个或两个描述导数估计类型的额外字段。objectivederivative 和（如果合适的话）constraintderivative 字段可以采用以下值：

"reverse-AD"，表示反向自动微分
"forward-AD"，表示正向自动微分
"finite-differences"，表示有限差分估计
"closed-form"，表示线性或二次函数

有关详细信息，请参阅Automatic Differentiation Background。

`lambda` — 解处的拉格朗日乘数
结构体

解处的拉格朗日乘数，以结构体形式返回。

注意

对于方程求解问题，solve 不返回 lambda。

对于 intlinprog 和 fminunc 求解器，lambda 为空，即 []。对于其他求解器，lambda 包含以下字段：

Variables - 对应于每个问题变量的字段。每个问题变量名称都是一个包含两个字段的结构体：
- Lower - 与变量的 LowerBound 属性关联的拉格朗日乘数，以与变量大小相同的数组形式返回。非零条目意味着解在下界处。这些乘数以如下结构表示：lambda.Variables.variablename.Lower。
- Upper - 与变量的 UpperBound 属性关联的拉格朗日乘数，以与变量大小相同的数组形式返回。非零条目意味着解在上界处。这些乘数以如下结构表示：lambda.Variables.variablename.Upper。
Constraints - 对应于每个问题约束的字段。每个问题约束的结构如下：字段名称为约束名称，值是与约束大小相同的数值数组。非零条目意味着约束在解处为活动状态。这些乘数以如下结构表示：lambda.Constraints.constraintname。
注意
约束数组的元素都具有相同的比较（<=、== 或 >=），并且均为相同的类型（线性、二次或非线性）。

算法

全部折叠

转换为求解器形式

在内部，solve 函数通过调用以下求解器求解优化问题。有关该问题的默认求解器和支持的求解器，请参阅 solvers 函数。调用 solve 时，您可以使用 'solver' 名称-值对组参数来覆盖默认值。

问题必须由 solve 或者由其他一些相关联的函数或对象转换为求解器形式，solve 才能调用求解器。这种转换需要一些条件，例如具有矩阵表示而不是优化变量表达式的线性约束。

算法的第一步是将优化表达式放入问题中。OptimizationProblem 对象有一个在其表达式中使用的变量的内部列表。每个变量在表达式中都有一个线性索引，并具有大小。因此，问题变量具有隐含的矩阵形式。prob2struct 函数执行从问题形式到求解器形式的转换。有关示例，请参阅将问题转换为结构体。

对于非线性优化问题，solve 使用自动微分计算目标函数和非线性约束函数的梯度。当目标函数和约束函数由 Supported Operations for Optimization Variables and Expressions 组成时，这些导数适用。当自动微分不适用时，求解器使用有限差分来估计导数。有关自动微分的详细信息，请参阅Automatic Differentiation Background。您可以使用 ObjectiveDerivative 名称-值参数控制 solve 如何使用自动微分。

有关 intlinprog 用于求解 MILP 问题的算法，请参阅intlinprog 算法。有关 linprog 用于求解线性规划问题的算法，请参阅线性规划算法。有关 quadprog 用于求解二次规划问题的算法，请参阅二次规划算法。有关线性或非线性最小二乘求解器算法，请参阅最小二乘（模型拟合）算法。有关非线性求解器算法，请参阅无约束非线性优化算法和约束非线性优化算法。有关 Global Optimization Toolbox 求解器算法的信息，请参阅 Global Optimization Toolbox 文档。

对于非线性方程求解，solve 在内部将每个方程表示为左右两侧之差。然后 solve 会尝试最小化方程分量的平方和。有关求解非线性方程组的算法，请参阅方程求解算法。当问题还有边界时，solve 调用 lsqnonlin 以最小化方程分量的平方和。请参阅最小二乘（模型拟合）算法。

注意

如果您的目标函数是一个平方和，并且您需要 solve 将其识别为平方和，请将其写为 norm(expr)^2 或 sum(expr.^2)，而不是 expr'*expr 或任何其他形式。内部解析器仅在平方和表示为范数的平方或显式平方和时才能识别平方和。有关详细信息，请参阅Write Objective Function for Problem-Based Least Squares。有关示例，请参阅Nonnegative Linear Least Squares, Problem-Based。

自动微分

在以下条件下，自动微分 (AD) 适用于 solve 和 prob2struct 函数：

目标函数和约束函数受支持，如Supported Operations for Optimization Variables and Expressions中所述。它们不需要使用 fcn2optimexpr 函数。
solve 调用的求解器是 fmincon、fminunc、fsolve 或 lsqnonlin。
对于优化问题，solve 或 prob2struct 的 'ObjectiveDerivative' 和 'ConstraintDerivative' 名称-值对组参数设置为 'auto'（默认值）、'auto-forward' 或 'auto-reverse'。
对于方程问题，'EquationDerivative' 选项设置为 'auto'（默认值）、'auto-forward' 或 'auto-reverse'。

AD 的适用情形	所有约束函数均受支持	一个或多个约束不受支持
目标函数受支持	AD 用于目标和约束	AD 仅用于目标
目标函数不受支持	AD 仅用于约束	不使用 AD

注意

对于线性或二次目标或约束函数，适用的求解器始终使用显函数梯度。这些梯度不是使用 AD 生成的。请参阅Closed Form。

当不满足这些条件时，solve 通过有限差分来估计梯度，prob2struct 不会在其生成的函数文件中创建梯度。

默认情况下，求解器选择以下 AD 类型：

对于一般的非线性目标函数，fmincon 默认选择反向 AD。对于非线性约束函数，如果其非线性约束的数量小于变量数目，fmincon 默认选择反向 AD。否则，fmincon 默认选择正向 AD。
对于一般的非线性目标函数，fminunc 默认选择反向 AD。
对于最小二乘目标函数，fmincon 和 fminunc 对目标函数默认选择正向 AD。有关基于问题的最小二乘目标函数的定义，请参阅Write Objective Function for Problem-Based Least Squares。
当目标向量中的元素数大于或等于变量数时，lsqnonlin 默认选择正向 AD。否则，lsqnonlin 默认选择反向 AD。
当方程数大于或等于变量数时，fsolve 默认选择正向 AD。否则，fsolve 默认选择反向 AD。

注意

要在由 prob2struct 转换的问题中使用自动导数，请传递指定这些导数的选项。

options = optimoptions('fmincon','SpecifyObjectiveGradient',true,...
    'SpecifyConstraintGradient',true);
problem.options = options;

当前，AD 仅适用于一阶导数；它不适用于二阶或更高阶导数。因此，在某些情况下（例如，如果您要使用解析黑塞矩阵来加速优化），您无法直接使用 solve，而必须使用Supply Derivatives in Problem-Based Workflow中所述的方法。

扩展功能

自动并行支持
通过使用 Parallel Computing Toolbox™ 自动运行并行计算来加快代码执行。

当非线性求解器的 UseParallel 选项为 true 时，solve 并行估计非线性求解器的导数。例如，

options = optimoptions('fminunc','UseParallel',true);
[sol,fval] = solve(prob,x0,'Options',options)

当所有目标和非线性约束函数仅由支持的运算（如Supported Operations for Optimization Variables and Expressions中所述）组成时，solve 不使用并行导数估计。在这种情况下，solve 使用自动微分来计算导数。请参阅自动微分。

通过将 'ObjectiveDerivative' 和 'ConstraintDerivative' 参数设置为 'finite-differences'，可以覆盖自动微分并以并行方式使用有限差分估计。

当您指定支持并行计算的 Global Optimization Toolbox 求解器（ga (Global Optimization Toolbox)、particleswarm (Global Optimization Toolbox)、patternsearch (Global Optimization Toolbox) 和 surrogateopt (Global Optimization Toolbox)）时，如果求解器的 UseParallel 选项为 true，则 solve 会执行并行计算。例如，

options = optimoptions("patternsearch","UseParallel",true);
[sol,fval] = solve(prob,x0,"Options",options,"Solver","patternsearch")

版本历史记录

在 R2017b 中推出

全部展开

R2018b: `solve(prob,solver)`、`solve(prob,options)` 和 `solve(prob,solver,options)` 语法已删除

要为 solve 选择选项或基础求解器，请使用名称-值对组。例如，

sol = solve(prob,'options',opts,'solver','quadprog');

上述语法不像名称-值对组那样灵活、标准或可扩展。

另请参阅

solve

语法

说明

示例

求解线性规划问题

使用基于问题的方法求解非线性规划问题

从初始点开始求解混合整数线性规划

基于问题指定 surrogateopt 的起点和值

基于问题使用多起点求解器最小化非线性函数

使用非默认选项求解整数规划问题

使用 intlinprog 求解线性规划

返回所有输出

用索引变量查看解

基于问题求解非线性方程组

输入参数

prob — 优化问题或方程问题 OptimizationProblem 对象 | EquationProblem 对象

x0 — 初始点 结构体 | OptimizationValues 对象的向量

ms — 多起点求解器 MultiStart 对象 | GlobalSearch 对象

名称-值参数

MinNumStartPoints — MultiStart 的最小起点数 20 (默认) | 正整数

Options — 优化选项 由 optimoptions 创建的对象 | options 结构体

ObjectiveDerivative — 对目标函数使用自动微分的指示 'auto' (默认) | 'auto-forward' | 'auto-reverse' | 'finite-differences'

ConstraintDerivative — 对约束函数使用自动微分的指示 'auto' (默认) | 'auto-forward' | 'auto-reverse' | 'finite-differences'

EquationDerivative — 对方程使用自动微分的指示 'auto' (默认) | 'auto-forward' | 'auto-reverse' | 'finite-differences'

输出参数

sol — 解 结构体 | OptimizationValues 向量

fval — 解处的目标函数值 实数 | 实数向量 | 实矩阵 | 结构体

exitflag — 求解器停止的原因 枚举变量

output — 有关优化过程的信息 结构体

lambda — 解处的拉格朗日乘数 结构体

算法

转换为求解器形式

自动微分

扩展功能

自动并行支持 通过使用 Parallel Computing Toolbox™ 自动运行并行计算来加快代码执行。

版本历史记录

R2018b: solve(prob,solver)、solve(prob,options) 和 solve(prob,solver,options) 语法已删除

另请参阅

主题

WeChat

基于问题指定 `surrogateopt` 的起点和值

使用 `intlinprog` 求解线性规划

`prob` — 优化问题或方程问题
`OptimizationProblem` 对象 | `EquationProblem` 对象

`x0` — 初始点
结构体 | `OptimizationValues` 对象的向量

`ms` — 多起点求解器
`MultiStart` 对象 | `GlobalSearch` 对象

`MinNumStartPoints` — `MultiStart` 的最小起点数
20 (默认) | 正整数

`Options` — 优化选项
由 `optimoptions` 创建的对象 | options 结构体

`ObjectiveDerivative` — 对目标函数使用自动微分的指示
`'auto'` (默认) | `'auto-forward'` | `'auto-reverse'` | `'finite-differences'`

`ConstraintDerivative` — 对约束函数使用自动微分的指示
`'auto'` (默认) | `'auto-forward'` | `'auto-reverse'` | `'finite-differences'`

`EquationDerivative` — 对方程使用自动微分的指示
`'auto'` (默认) | `'auto-forward'` | `'auto-reverse'` | `'finite-differences'`

`sol` — 解
结构体 | `OptimizationValues` 向量

`fval` — 解处的目标函数值
实数 | 实数向量 | 实矩阵 | 结构体

`exitflag` — 求解器停止的原因
枚举变量

`output` — 有关优化过程的信息
结构体

`lambda` — 解处的拉格朗日乘数
结构体

自动并行支持
通过使用 Parallel Computing Toolbox™ 自动运行并行计算来加快代码执行。

R2018b: `solve(prob,solver)`、`solve(prob,options)` 和 `solve(prob,solver,options)` 语法已删除