无约束非线性优化算法
无约束优化定义
无约束最小化问题求向量 x,使得标量函数 f(x) 取得局部最小值:
无约束意味着对 x 的范围没有限制。
fminunc trust-region 算法
非线性最小化信赖域方法
Optimization Toolbox™ 求解器中使用的许多方法都基于信赖域,这是一个简单而功能强大的优化概念。
要理解信赖域优化方法,请考虑无约束最小化问题,最小化 f(x),该函数接受向量参量并返回标量。假设您现在位于 n 维空间中的点 x 处,并且您要寻求改进,即移至函数值较低的点。基本思路是用较简单的函数 q 来逼近 f,该函数需能充分反映函数 f 在点 x 的邻域 N 中的行为。此邻域是信赖域。试探步 s 是通过在 N 上进行最小化(或近似最小化)来计算的。以下是信赖域子问题,
| (1) |
如果 f(x + s) < f(x),当前点更新为 x + s;否则,当前点保持不变,信赖域 N 缩小,算法再次计算试探步。
在定义特定信赖域方法以最小化 f(x) 的过程中,关键问题是如何选择和计算逼近 q(在当前点 x 上定义)、如何选择和修改信赖域 N,以及如何准确求解信赖域子问题。本节重点讨论无约束问题。后面的章节讨论由于变量约束的存在而带来的额外复杂性。
在标准信赖域方法 ([48]) 中,二次逼近 q 由 F 在 x 处的泰勒逼近的前两项定义;邻域 N 通常是球形或椭圆形。以数学语言表述,信赖域子问题通常写作
| (2) |
其中,g 是 f 在当前点 x 处的梯度,H 是黑塞矩阵(二阶导数的对称矩阵),D 是对角缩放矩阵,Δ 是正标量,‖ . ‖ 是 2-范数。存在求解公式 2 的好算法(请参阅[48]);此类算法通常涉及计算 H 的所有特征值,并将牛顿法应用于以下久期方程
此类算法提供公式 2 的精确解。但是,它们要耗费与 H 的几个分解成比例的时间。因此,对于大型问题,需要一种不同方法。文献([42] 和 [50])中提出了几种基于公式 2 的逼近和启发式方法建议。Optimization Toolbox 求解器采用的逼近方法是将信赖域子问题限制在二维子空间 S 内([39] 和 [42])。一旦计算出子空间 S,即使需要完整的特征值/特征向量信息,求解公式 2 的工作量也不大(因为在子空间中,问题只是二维的)。现在的主要工作已转移到子空间的确定上。
二维子空间 S 是借助下述预条件共轭梯度法确定的。求解器将 S 定义为由 s1 和 s2 确定的线性空间,其中 s1 是梯度 g 的方向,s2 是近似牛顿方向,即下式的解
| (3) |
或是负曲率的方向,
| (4) |
以此种方式选择 S 背后的理念是强制全局收敛(通过最陡下降方向或负曲率方向)并实现快速局部收敛(通过牛顿步,如果它存在)。
现在,我们可以很容易地给出基于信赖域的无约束最小化的大致框架:
构造二维信赖域子问题。
求解公式 2 以确定试探步 s。
如果 f(x + s) < f(x),则 x = x + s。
调整 Δ。
重复这四个步骤,直到收敛。信赖域维度 Δ 根据标准规则进行调整。具体来说,它会在试探步不被接受(即 f(x + s) ≥ f(x))时减小。有关这方面的讨论,请参阅[46] 和 [49]。
Optimization Toolbox 求解器用专用函数处理 f 的一些重要特例:非线性最小二乘、二次函数和线性最小二乘。然而,其底层算法思路与一般情况相同。这些特例将在后面的章节中讨论。
预条件共轭梯度法
求解大型对称正定线性方程系统 Hp = –g 的一种常用方法是预条件共轭梯度法 (PCG)。这种迭代方法需要能够计算 H·v 形式的矩阵-向量积,其中 v 是任意向量。对称正定矩阵 M 是 H 的预条件子。也就是说,M = C2,其中 C–1HC–1 是良态矩阵或具有聚类特征值的矩阵。
在最小化上下文中,您可以假设黑塞矩阵 H 是对称矩阵。然而,只有在强最小值点的邻域内才能保证 H 是正定矩阵。算法 PCG 在遇到负(或零)曲率方向(即 dTHd ≤ 0)时退出。PCG 输出方向 p 要么是负曲率方向,要么是牛顿方程组 Hp = –g 的近似解。无论哪种情况,p 都有助于定义在非线性最小化信赖域方法中讨论的信赖域方法中使用的二维子空间。
fminunc quasi-newton 算法
无约束优化的基础知识
尽管有很多方法可用于无约束优化,但可以根据使用或不使用导数信息对这些方法进行大致分类。仅使用函数计算的搜索方法(例如内尔德和米德的论著 [30] 所述的单纯形搜索)最适合不平滑或有许多不连续点的问题。当要最小化的函数的一阶导数连续时,梯度法通常更高效。高阶方法,例如牛顿法,仅在二阶信息具备且容易计算时才真正适用,因为使用数值微分计算二阶信息的计算成本高昂。
梯度法使用关于函数斜率的信息来决定搜索方向,该方向是最小值预计所在的方向。其中最简单的是最陡下降法,即在 –∇f(x) 方向上进行搜索,其中 ∇f(x) 是目标函数的梯度。当要最小化的函数具有狭长的谷部时,这种方法效率很低,罗森布罗克函数就是一个例子
| (5) |
此函数的最小值位于 x = [1,1] 处,在该处 f(x) = 0。下图显示了此函数的等高线图,以及从点 [–2,2] 开始、使用最陡下降法获得的最小值解路径。优化在 400 次迭代后终止,离最小值仍有相当大的距离。图中的黑色区域是方法从谷部的一侧蜿蜒到另一侧所形成的。
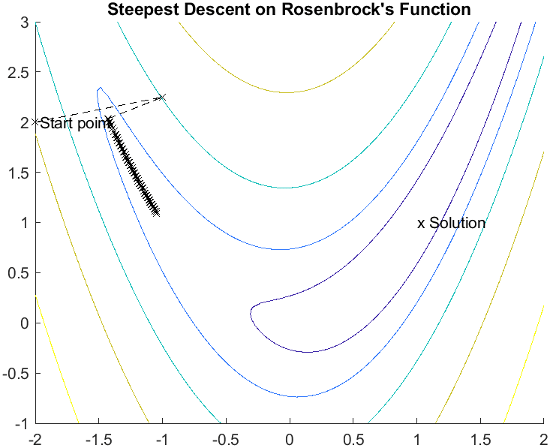
此函数也称为香蕉函数,因其在原点附近的弯曲方式,成为无约束优化中出名的难题。罗森布罗克函数在本节中多次出现,用于展示各种优化方法的用法。由于 U 形谷部两侧的斜率陡峭,绘制的等高线呈现指数递增。
有关此图的更完整说明,包括生成迭代点的脚本,请参阅香蕉函数的最小化。
拟牛顿法
在使用梯度信息的方法中,最受欢迎的是拟牛顿法。这些方法在每次迭代中构建曲率信息,以如下形式表示二次模型问题:
| (6) |
其中,黑塞矩阵 H 是正定对称矩阵,c 是常向量,b 是常数。当 x 的偏导数为零时,出现此问题的最优解,即:
| (7) |
最优解点 x* 可以写为
| (8) |
牛顿法(与拟牛顿法相反)直接计算 H,并在多次迭代后沿下降方向前进以定位最小值。对 H 进行数值计算的运算量非常大。拟牛顿法可避免这种情况,它根据观察到的 f(x) 和 ∇f(x) 的行为来构建曲率信息,以使用适当的更新方法来逼近 H。
人们开发了大量的黑塞函数更新方法。不过,求解一般问题时,通常认为布罗伊登 [3]、弗莱彻 [12]、戈德法布 [20] 和沙诺 [37] (BFGS) 的公式最为高效。
BFGS 给出的公式是
| (9) |
其中
作为起点,H0 可以设置为任何对称正定矩阵,例如单位矩阵 I。梯度信息或者通过解析计算的梯度提供,或者通过有限差分使用数值微分方法由偏导数推出。这涉及到依次扰动每个设计变量 x 并计算目标函数的变化率。
在每个主迭代 k 中,都会在以下方向上执行线搜索
| (10) |
为了避免对黑塞函数 H 求逆,您可以推导出一种更新方法,该方法避免对 H 直接求逆,方法是使用一个公式,在每次更新时取黑塞逆矩阵 H–1 的近似。一种著名的方法是戴维登[7]、弗莱彻和鲍威尔[14] 的 DFP 公式。除了用 qk 取代 sk 之外,该方法使用的公式与 BFGS 方法使用的公式 (公式 9) 相同。
罗森布罗克函数的解路径展示了拟牛顿法的过程。该方法能够配合谷部的形状进行调整,它仅使用有限差分梯度,在大约 150 次函数计算后收敛于最小值。
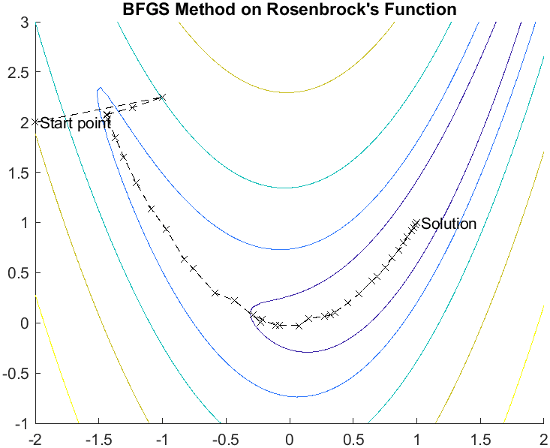
有关此图的更完整说明,包括生成迭代点的脚本,请参阅香蕉函数的最小化。
线搜索
线搜索是一种搜索方法,用作主优化算法的一部分。在主算法的每一步,线搜索方法沿包含当前点 xk 的线进行搜索,平行于搜索方向,该方向是由主算法确定的向量。也就是说,该方法计算下一个迭代 xk+1,形式如下:
| (11) |
其中,xk 表示当前迭代,dk 表示搜索方向,α* 表示标量步长参数。
线搜索方法尝试通过反复最小化目标函数的多项式插值模型来减小沿线 xk + α*dk 的目标函数。线搜索过程包含两个主要步骤:
包围阶段确定要搜索的 线上的点的范围。包围对应于指定 α 值范围的区间。
分段步骤将包围划分为多个子区间,在此基础上通过多项式插值逼近目标函数的最小值。
所得步长 α 满足沃尔夫条件:
| (12) |
| (13) |
其中,c1 和 c2 是常数且 0 < c1 < c2 < 1。
第一个条件 (公式 12) 要求 αk 充分减小目标函数。第二个条件(公式 13)确保步长不至于太小。同时满足两个条件(公式 12 和公式 13)的点称为可接受点。
黑塞矩阵更新
许多优化函数通过使用 BFGS 方法(公式 9)在每次迭代中更新黑塞函数来确定搜索方向。函数 fminunc 还允许您使用 DFP 方法(见拟牛顿法),要选择 DFP 方法,请在 options 中将 HessUpdate 设置为 'dfp'。黑塞矩阵 H 始终保持为正定矩阵,因此搜索方向 d 始终是下降方向。这意味着,对于 d 方向上某个任意小的步长 α,目标函数的模会减小。通过确保 H 初始化为正定矩阵,然后确保 (由公式 14 给出)始终为正,您可以确保 H 正定。项 是以下两个项的乘积:线搜索步长参数 αk,以及搜索方向 d 与过去和现在梯度计算值的组合,即
| (14) |
通过执行足够准确的线搜索,您总能达到 为正的条件。这是因为搜索方向 d 是下降方向,所以 αk 和负梯度 –∇f(xk)Td 始终为正。因此,通过提高线搜索的准确度,可以将可能的负项 –∇f(xk+1)Td 的模尽可能减小至所需程度。
LBFGS黑塞函数逼近
对于大型问题,BFGS黑塞函数逼近方法可能相对较慢,并会占用大量内存。为了避免这些问题,请通过将 HessianApproximation 选项设置为 'lbfgs' 来使用 LBFGS黑塞函数逼近。这会导致 fminunc 使用占用内存较少的 BFGS黑塞函数逼近,如下所述。关于在大型问题中使用 LBFGS 的好处,请参阅求解多变量非线性问题。
如 Nocedal 和 Wright [31] 中所述,占用内存较少的 BFGS黑塞函数逼近类似于 拟牛顿法 中所述的 BFGS 逼近,但在之前的迭代中使用有限的内存。公式 9 中给出的黑塞函数更新公式为
其中
BFGS 过程的另一个描述是
| (15) |
其中 ɑk 是通过线搜索选择的步长,Hk 是逆黑塞函数逼近。Hk 的公式为:
其中 sk 和 qk 的定义如前所示,并且
对于 LBFGS 算法,该算法从紧邻的前次迭代中保留固定有限的前 m 个参数 sk 和 qk 。从初始的 H0 开始,该算法计算近似的 Hk 以从 公式 15 获得步长。将 ρj、qj 和 sj 的最近 m 个值代入前面的方程,以递归形式计算 。有关详细信息,请参阅 Nocedal 和 Wright [31] 的算法 7.4。
