fminunc

求无约束多变量函数的最小值

全页折叠

语法

x = fminunc(fun,x0)

x = fminunc(fun,x0,options)

x = fminunc(problem)

[x,fval] = fminunc(___)

[x,fval,exitflag,output] = fminunc(___)

[x,fval,exitflag,output,grad,hessian] = fminunc(___)

说明

非线性规划求解器。

求以下问题的最小值：

$\min_{x} f (x)$

其中，f(x) 是返回标量的函数。

x 是向量或矩阵；请参阅矩阵参量。

x = fminunc(fun,x0) 在点 x0 处开始并尝试求 fun 中描述的函数的局部最小值 x。点 x0 可以是标量、向量或矩阵。

注意

传递额外参数说明如何将额外的参数传递给目标函数和非线性约束函数（如有必要）。

fminunc 适用于无约束非线性问题。如果您的问题有约束，通常使用 fmincon。请参阅优化决策表。

示例

x = fminunc(fun,x0,options) 使用 options 中指定的优化选项最小化 fun。使用 optimoptions 可设置这些选项。

示例

x = fminunc(problem) 求 problem 的最小值，它是 problem 中所述的一个结构体。

示例

[x,fval] = fminunc(___) 对上述任何语法，返回目标函数 fun 在解 x 处的值。

示例

[x,fval,exitflag,output] = fminunc(___) 还返回描述 fminunc 的退出条件的值 exitflag，以及提供优化过程信息的结构体 output。

示例

[x,fval,exitflag,output,grad,hessian] = fminunc(___) 还返回：

grad - fun 在解 x 处的梯度。
hessian - fun 在解 x 处的黑塞矩阵。请参阅fminunc黑塞函数。

示例

全部折叠

最小化多项式

打开实时脚本

最小化函数： $f (x) = 3 x_{1}^{2} + 2 x_{1} x_{2} + x_{2}^{2} - 4 x_{1} + 5 x_{2}$ 。

为此，编写用于计算目标的匿名函数 fun。

fun = @(x)3*x(1)^2 + 2*x(1)*x(2) + x(2)^2 - 4*x(1) + 5*x(2);

调用 fminunc 以在 [1,1] 附近处求 fun 的最小值。

x0 = [1,1];
[x,fval] = fminunc(fun,x0)

Local minimum found.

Optimization completed because the size of the gradient is less than
the value of the optimality tolerance.

<stopping criteria details>

x = 1×2

    2.2500   -4.7500

fval = 
-16.3750

提供梯度

打开实时脚本

当您提供导数时，fminunc 可以执行得更快、也更可靠。

编写返回梯度和函数值的目标函数。使用包括梯度和黑塞函数中所述的条件化形式。目标函数是罗森布罗克函数，

$f (x) = 100 {(x_{2} - x_{1}^{2})}^{2} + (1 - x_{1})^{2},$

它有梯度

$\nabla f (x) = [\begin{array}{cccccccccccccccccccc} - 400 (x_{2} - x_{1}^{2}) x_{1} - 2 (1 - x_{1}) \\ 200 (x_{2} - x_{1}^{2}) \end{array}]$ .

具有梯度的目标函数的代码出现在此示例的末尾。

创建使用目标函数的梯度的选项。此外，将算法设置为 'trust-region'。

options = optimoptions('fminunc','Algorithm','trust-region','SpecifyObjectiveGradient',true);

将初始点设置为 [-1,2]。然后调用 fminunc。

x0 = [-1,2];
fun = @rosenbrockwithgrad;
x = fminunc(fun,x0,options)

Local minimum found.

Optimization completed because the size of the gradient is less than
the value of the optimality tolerance.

<stopping criteria details>

x = 1×2

    1.0000    1.0000

以下代码创建 rosenbrockwithgrad 函数，该函数包含梯度作为第二个输出。

function [f,g] = rosenbrockwithgrad(x)
% Calculate objective f
f = 100*(x(2) - x(1)^2)^2 + (1-x(1))^2;

if nargout > 1 % gradient required
    g = [-400*(x(2)-x(1)^2)*x(1) - 2*(1-x(1));
        200*(x(2)-x(1)^2)];
end
end

使用问题结构体

打开实时脚本

使用问题结构体而不是单独的参量来求解与提供梯度中相同的问题。

编写返回梯度和函数值的目标函数。使用包括梯度和黑塞函数中所述的条件化形式。目标函数是罗森布罗克函数，

$f (x) = 100 {(x_{2} - x_{1}^{2})}^{2} + (1 - x_{1})^{2}$ ,

它有梯度

$\nabla f (x) = [\begin{array}{cccccccccccccccccccc} - 400 (x_{2} - x_{1}^{2}) x_{1} - 2 (1 - x_{1}) \\ 200 (x_{2} - x_{1}^{2}) \end{array}]$ .

具有梯度的目标函数的代码出现在此示例的末尾。

创建使用目标函数的梯度的选项。此外，将算法设置为 'trust-region'。

options = optimoptions('fminunc','Algorithm','trust-region','SpecifyObjectiveGradient',true);

创建包括初始点 x0 = [-1,2] 的问题结构体。有关此结构体中的必填字段，请参阅problem。

problem.options = options;
problem.x0 = [-1,2];
problem.objective = @rosenbrockwithgrad;
problem.solver = 'fminunc';

求解。

x = fminunc(problem)

Local minimum found.

Optimization completed because the size of the gradient is less than
the value of the optimality tolerance.

<stopping criteria details>

x = 1×2

    1.0000    1.0000

以下代码创建 rosenbrockwithgrad 函数，该函数包含梯度作为第二个输出。

function [f,g] = rosenbrockwithgrad(x)
% Calculate objective f
f = 100*(x(2) - x(1)^2)^2 + (1-x(1))^2;

if nargout > 1 % gradient required
    g = [-400*(x(2)-x(1)^2)*x(1)-2*(1-x(1));
        200*(x(2)-x(1)^2)];
end
end

获得最佳目标函数值

打开实时脚本

求非线性函数最小值的位置和该最小值处的函数值。目标函数是

$f (x) = x (1) e^{- {‖ x ‖}_{2}^{2}} + {‖ x ‖}_{2}^{2} / 20$ .

fun = @(x)x(1)*exp(-(x(1)^2 + x(2)^2)) + (x(1)^2 + x(2)^2)/20;

从 x0 = [1,2] 开始查找最小值点的位置和对应的目标函数值。

x0 = [1,2];
[x,fval] = fminunc(fun,x0)

Local minimum found.

Optimization completed because the size of the gradient is less than
the value of the optimality tolerance.

<stopping criteria details>

x = 1×2

   -0.6691    0.0000

fval = 
-0.4052

检查求解过程

打开实时脚本

选择 fminunc 选项和输出来检查求解过程。

设置选项以获取迭代输出并使用 'quasi-newton' 算法。

options = optimoptions(@fminunc,'Display','iter','Algorithm','quasi-newton');

目标函数是

$f (x) = x (1) e^{- {‖ x ‖}_{2}^{2}} + {‖ x ‖}_{2}^{2} / 20 .$

fun = @(x)x(1)*exp(-(x(1)^2 + x(2)^2)) + (x(1)^2 + x(2)^2)/20;

在 x0 = [1,2] 处开始最小化，并获取能够有助您检查求解质量和过程的输出。

x0 = [1,2];
[x,fval,exitflag,output] = fminunc(fun,x0,options)

                                                        First-order 
 Iteration  Func-count       f(x)        Step-size       optimality
     0           3         0.256738                         0.173
     1           6         0.222149              1          0.131  
     2           9          0.15717              1          0.158  
     3          18        -0.227902       0.438133          0.386  
     4          21        -0.299271              1           0.46  
     5          30        -0.404028       0.102071         0.0458  
     6          33        -0.404868              1         0.0296  
     7          36        -0.405236              1        0.00119  
     8          39        -0.405237              1       0.000252  
     9          42        -0.405237              1       7.97e-07  

Local minimum found.

Optimization completed because the size of the gradient is less than
the value of the optimality tolerance.

<stopping criteria details>

x = 1×2

   -0.6691    0.0000

fval = 
-0.4052

exitflag = 
1

output = struct with fields:
       iterations: 9
        funcCount: 42
         stepsize: 2.9343e-04
     lssteplength: 1
    firstorderopt: 7.9721e-07
        algorithm: 'quasi-newton'
          message: 'Local minimum found.↵↵Optimization completed because the size of the gradient is less than↵the value of the optimality tolerance.↵↵<stopping criteria details>↵↵Optimization completed: The first-order optimality measure, 6.796073e-07, is less ↵than options.OptimalityTolerance = 1.000000e-06.'

退出标志 1 表明该解是局部最优解。
output 结构体显示迭代次数、函数计算次数和其他信息。
迭代输出还会提供迭代次数和函数计算次数。

使用 `"lbfgs"` 黑塞矩阵逼近求解大型问题

如果您的问题涉及诸多变量，HessianApproximation 的默认值会导致 fminunc 使用大量内存并且运行缓慢。要减少内存使用并加快运行速度，请指定 HessianApproximation="lbfgs"。

例如，如果您尝试使用默认参数最小化具有 1e5 变量的 multirosenbrock 函数（如下所列），fminunc 会引发错误。

N = 1e5;
x0 = -2*ones(N,1);
x0(2:2:N) = 2;
[x,fval] = fminunc(@multirosenbrock,x0)

Error using eye
Requested 100000x100000 (74.5GB) array exceeds maximum array size preference (63.9GB). This might cause MATLAB to become
unresponsive.

Error in optim.internal.fminunc.AbstractDenseHessianApproximation (line 21)
        this.Value = eye(nVars);

Error in optim.internal.fminunc.BFGSHessianApproximation (line 14)
        this = this@optim.internal.fminunc.AbstractDenseHessianApproximation(nVars);

Error in fminusub (line 73)
    HessApprox = optim.internal.fminunc.BFGSHessianApproximation(sizes.nVar);

Error in fminunc (line 488)
   [x,FVAL,GRAD,HESSIAN,EXITFLAG,OUTPUT] = fminusub(funfcn,x, ...

要求解此问题，请将 HessianApproximation 选项设置为 "lbfgs"。要加速求解，请设置选项以使用提供的梯度。

N = 1e5;
x0 = -2*ones(N,1);
x0(2:2:N) = 2;
options = optimoptions("fminunc",HessianApproximation="lbfgs",...
    SpecifyObjectiveGradient=true);
[x,fval] = fminunc(@multirosenbrock,x0,options);

Local minimum found.

Optimization completed because the size of the gradient is less than
the value of the optimality tolerance.

对于所有 i，理论解是 x(i) = 1。检查返回的解的精确度。

max(abs(x-1))

ans =

   1.3795e-04

使用以下代码创建 multirosenbrock 函数。

function [f,g] = multirosenbrock(x)
% Get the problem size
n = length(x);  
if n == 0, error('Input vector, x, is empty.'); end
if mod(n,2) ~= 0
   error('Input vector, x ,must have an even number of components.');
end
% Evaluate the vector function
odds  = 1:2:n;
evens = 2:2:n;
F = zeros(n,1);
F(odds,1)  = 1-x(odds);
F(evens,1) = 10.*(x(evens)-x(odds).^2); 
f = sum(F.^2);
if nargout >= 2 % Calculate gradient
    g = zeros(n,1);
    g(evens) = 200*(x(evens)-x(odds).^2);
    g(odds) = -2*(1 - x(odds)) - 400*(x(evens)-x(odds).^2).*x(odds);
end
end

输入参数

全部折叠

`fun` — 最小化的函数
函数句柄 | 函数名称

要最小化的函数，指定为函数句柄或函数名称。fun 函数接受向量或数组 x，并返回实数标量 f，即在 x 处计算的目标函数值。

fminunc 以 x0 参量的形状将 x 传递给目标函数。例如，如果 x0 是 5×3 数组，则 fminunc 将 x 以 5×3 数组的形式传递给 fun。

将 fun 指定为文件的函数句柄：

x = fminunc(@myfun,x0)

其中 myfun 是一个 MATLAB^® 函数，例如

function f = myfun(x)
f = ...            % Compute function value at x

您还可以为匿名函数指定 fun 作为函数句柄：

x = fminunc(@(x)norm(x)^2,x0);

如果您可以计算 fun 的梯度且 SpecifyObjectiveGradient 选项设置为 true，设置如下

options = optimoptions('fminunc','SpecifyObjectiveGradient',true)

则 fun 必须在第二个输出参量中返回梯度向量 g(x)。

如果您还可以计算黑塞矩阵，并通过 options = optimoptions('fminunc','HessianFcn','objective') 将 HessianFcn 选项设置为 'objective'，且将 Algorithm 选项设置为 'trust-region'，则 fun 必须在第三个输出参量中返回黑塞值 H(x)，即一个对称矩阵。fun 可以给出稀疏黑塞矩阵。有关详细信息，请参阅适用于 fminunc 信赖域或 fmincon 信赖域反射算法的黑塞函数。

trust-region 算法允许您提供黑塞矩阵乘法函数。此函数给出黑塞乘以向量的乘积结果，而不直接计算黑塞矩阵。这可以节省内存。请参阅黑塞矩阵乘法函数。

示例: fun = @(x)sin(x(1))*cos(x(2))

数据类型: char | function_handle | string

`x0` — 初始点
实数向量 | 实数数组

初始点，指定为实数向量或实数数组。求解器使用 x0 中的元素数量和 x0 的大小来确定 fun 接受的变量数量和大小。

示例: x0 = [1,2,3,4]

数据类型: double

`options` — 优化选项
`optimoptions` 的输出 | 结构体，例如 `optimset` 返回的结构体

优化选项，指定为 optimoptions 的输出或 optimset 等返回的结构体。

一些选项适用于所有算法，其他选项则与特定算法相关。有关详细信息，请参阅优化选项参考。

optimoptions 显示中缺少某些选项。这些选项在下表中以斜体显示。有关详细信息，请参阅查看优化选项。

所有算法
`Algorithm`	选择 `fminunc` 算法。选项是 `'quasi-newton'`（默认值）或 `'trust-region'`。 `'trust-region'` 算法要求您提供梯度（请参阅 `fun` 的说明），否则 `fminunc` 将使用 `'quasi-newton'` 算法。有关选择算法的信息，请参阅选择算法。
CheckGradients	将用户提供的导数（目标的梯度）与有限差分导数进行比较。选项是 `false`（默认值）或 `true`。对于 `optimset`，名称为 `DerivativeCheck`，值为 `'on'` 或 `'off'`。请参阅当前选项名称和旧选项名称。以后的版本中将会删除 `CheckGradients` 选项。要检查导数，请使用 `checkGradients` 函数。
Diagnostics	显示关于要最小化或求解的函数的诊断信息。选项是 `'off'`（默认值）或 `'on'`。
DiffMaxChange	有限差分梯度变量的最大变化（正标量）。默认值为 `Inf`。
DiffMinChange	有限差分梯度变量的最小变化（正标量）。默认值为 `0`。
`Display`	显示级别（请参阅迭代输出）： `'off'` 或 `'none'` 不显示输出。 `'iter'` 显示每次迭代的输出，并给出默认退出消息。 `'iter-detailed'` 显示每次迭代的输出，并给出带有技术细节的退出消息。 `'notify'` 仅当函数不收敛时才显示输出，并给出默认退出消息。 `'notify-detailed'` 仅当函数不收敛时才显示输出，并给出技术性退出消息。 `'final'`（默认值）仅显示最终输出，并给出默认退出消息。 `'final-detailed'` 仅显示最终输出，并给出带有技术细节的退出消息。
`FiniteDifferenceStepSize`	有限差分的标量或向量步长因子。当您将 `FiniteDifferenceStepSize` 设置为向量 `v` 时，正向有限差分 `delta` 是 `delta = v.sign′(x).max(abs(x),TypicalX);` 其中 `sign′(x) = sign(x)`（例外是 `sign′(0) = 1`）。中心有限差分是 `delta = v.*max(abs(x),TypicalX);` 标量 `FiniteDifferenceStepSize` 扩展为向量。对于正向有限差分，默认值为 `sqrt(eps)`；对于中心有限差分，默认值为 `eps^(1/3)`。仅当 `CheckGradients` 设置为 `true` 时，信赖域算法才使用 `FiniteDifferenceStepSize`。对于 `optimset`，名称是 `FinDiffRelStep`。请参阅当前选项名称和旧选项名称。
`FiniteDifferenceType`	用于估计梯度的有限差分是 `'forward'`（默认值）或 `'central'`（中心化）。`'central'` 需要两倍的函数计算次数，但应更准确。仅当 `CheckGradients` 设置为 `true` 时，信赖域算法才使用 `FiniteDifferenceType`。对于 `optimset`，名称是 `FinDiffType`。请参阅当前选项名称和旧选项名称。
FunValCheck	检查目标函数值是否有效。默认设置 `'off'` 不执行检查。当目标函数返回的值是 `complex`、`Inf` 或 `NaN` 时，`'on'` 设置显示错误。
`MaxFunctionEvaluations`	允许的最大函数计算次数，非负整数。默认值为 `100*numberOfVariables`。请参阅容差和停止条件和迭代和函数计算次数。对于 `optimset`，名称是 `MaxFunEvals`。请参阅当前选项名称和旧选项名称。
`MaxIterations`	允许的最大迭代次数，非负整数。默认值为 `400`。请参阅容差和停止条件和迭代和函数计算次数。对于 `optimset`，名称是 `MaxIter`。请参阅当前选项名称和旧选项名称。
`OptimalityTolerance`	一阶最优性的终止容差（非负标量）。默认值为 `1e-6`。请参阅一阶最优性测度。对于 `optimset`，名称是 `TolFun`。请参阅当前选项名称和旧选项名称。
`OutputFcn`	指定优化函数在每次迭代中调用的一个或多个用户定义的函数。传递函数句柄或函数句柄的元胞数组。默认值是“无”(`[]`)。请参阅输出函数和绘图函数语法。
`PlotFcn`	对算法执行过程中的各种进度测量值绘图，可以选择预定义的绘图，也可以自行编写绘图函数。传递内置绘图函数名称、函数句柄或由内置绘图函数名称或函数句柄组成的元胞数组。对于自定义绘图函数，传递函数句柄。默认值是“无”(`[]`)： `'optimplotx'` 绘制当前点。 `'optimplotfunccount'` 绘制函数计数。 `'optimplotfval'` 绘制函数值。 `'optimplotstepsize'` 绘制步长。 `'optimplotfirstorderopt'` 绘制一阶最优性测度。自定义绘图函数使用与输出函数相同的语法。请参阅Optimization Toolbox 的输出函数和输出函数和绘图函数语法。对于 `optimset`，名称是 `PlotFcns`。请参阅当前选项名称和旧选项名称。
`SpecifyObjectiveGradient`	用户定义的目标函数梯度。请参阅 `fun` 的说明，了解如何在 `fun` 中定义梯度。设置为 `true`，以使 `fminunc` 采用用户定义的目标函数梯度。默认值 `false` 会导致 `fminunc` 使用有限差分来估计梯度。您必须提供梯度，并将 `SpecifyObjectiveGradient` 设置为 `true` 才能使用信赖域算法。拟牛顿算法不需要此选项。对于 `optimset`，名称为 `GradObj`，值为 `'on'` 或 `'off'`。请参阅当前选项名称和旧选项名称。
`StepTolerance`	`x` 的终止容差，非负标量。默认值为 `1e-6`。请参阅容差和停止条件。对于 `optimset`，名称是 `TolX`。请参阅当前选项名称和旧选项名称。
`TypicalX`	典型的 `x` 值。`TypicalX` 中的元素数等于 `x0`（即起点）中的元素数。默认值为 `ones(numberofvariables,1)`。`fminunc` 使用 `TypicalX` 缩放有限差分来进行梯度估计。 `trust-region` 算法仅对 `CheckGradients` 选项使用 `TypicalX`。
`trust-region` 算法
`FunctionTolerance`	函数值的终止容差，非负标量。默认值为 `1e-6`。请参阅容差和停止条件。对于 `optimset`，名称是 `TolFun`。请参阅当前选项名称和旧选项名称。
`HessianFcn`	如果设置为 `[]`（默认值），`fminunc` 使用有限差分逼近黑塞矩阵。如果设置为 `'objective'`，`fminunc` 对目标函数使用用户定义的黑塞矩阵。黑塞矩阵是目标函数的第三个输出（请参阅 `fun`）。对于 `optimset`，名称是 `HessFcn`。请参阅当前选项名称和旧选项名称。
`HessianMultiplyFcn`	黑塞矩阵乘法函数，指定为函数句柄。对于大规模结构问题，此函数计算黑塞矩阵乘积 `HY`，而并不实际构造 `H`。函数的形式是 W = hmfun(Hinfo,Y) 其中 `Hinfo` 包含用于计算 `HY` 的矩阵。上述第一个参量与目标函数 `fun` 返回的第三个参量相同，例如 [f,g,Hinfo] = fun(x) `Y` 是矩阵，其行数与问题中的维数相同。矩阵 `W = H*Y`（尽管其中 `H` 未显式构造）。`fminunc` 使用 `Hinfo` 计算预条件子。要了解如何为 `hmfun` 所需的额外参数提供值的信息，请参阅传递额外参数。注意要使用 `HessianMultiplyFcn` 选项，`HessianFcn` 必须设置为 `[]`。有关示例，请参阅使用密集结构 Hessian 和线性等式进行最小化。对于 `optimset`，名称是 `HessMult`。请参阅当前选项名称和旧选项名称。
HessPattern	用于有限差分的黑塞矩阵稀疏模式。如果存在 ∂²`fun`/∂`x(i)`∂`x(j)` ≠ 0，则设置 `HessPattern(i,j) = 1`。否则，设置 `HessPattern(i,j) = 0`。如果不方便在 `fun` 中计算黑塞矩阵 `H`，但您可以确定（例如，通过检查）`fun` 的梯度的第 `i` 个分量何时依赖 `x(j)`，请使用 `HessPattern`。如果您提供 `H` 的稀疏结构作为 `HessPattern` 的值，`fminunc` 可以通过稀疏有限差分（梯度）逼近 `H`。这相当于提供非零元的位置。当结构未知时，不要设置 `HessPattern`。默认行为是将 `HessPattern` 视为由 1 组成的稠密矩阵。然后，`fminunc` 在每次迭代中计算满有限差分逼近。对于大型问题，这种计算可能成本高昂，因此通常最好确定稀疏结构。
MaxPCGIter	预条件共轭梯度 (PCG) 迭代的最大次数，正标量。默认值为 `max(1,floor(numberOfVariables/2))`。有关详细信息，请参阅信赖域算法。
PrecondBandWidth	PCG 的预条件子上带宽，非负整数。默认情况下，`fminunc` 使用对角预条件处理（上带宽为 0）。对于某些问题，增加带宽会减少 PCG 迭代次数。将 `PrecondBandWidth` 设置为 `Inf` 会使用直接分解（乔列斯基分解），而不是共轭梯度 (CG)。直接分解的计算成本较 CG 高，但所得的求解步质量更好。
`SubproblemAlgorithm`	确定迭代步的计算方式。与 `'factorization'` 相比，默认值 `'cg'` 采用的步执行速度更快，但不够准确。请参阅fminunc trust-region 算法。
TolPCG	PCG 迭代的终止容差，正标量。默认值为 `0.1`。
`quasi-newton` 算法
`HessianApproximation`	指定 `fminunc` 计算黑塞矩阵的方法。选项包括： `"bfgs"`（默认值） `"lbfgs"` `{"lbfgs",Positive Integer}` 选择项 `"lbfgs"` 与 `{"lbfgs",10}` 相同，表明 `"lbfgs"` 的默认内存值是 `10`。使用 `"lbfgs"` 求解多变量问题。请参阅求解多变量非线性问题。对于 `optimset`，选项名称为 HessUpdate，值为 `"bfgs"`、`"lbfgs"`、`{"lbfgs",Positive Integer}`、`"dfp"` 和 `"steepdesc"`。请参阅当前选项名称和旧选项名称。注意通常情况下，`"dfp"` 和 `"steepdesc"` 值不适用于实际工作。它们可用于教育用途；请参阅香蕉函数的最小化。
`ObjectiveLimit`	容差（停止条件），标量。如果迭代中的目标函数值小于或等于 `ObjectiveLimit`，迭代将停止，因为问题可能是无界的。默认值为 `-1e20`。
`UseParallel`	此选项为 `true` 时，`fminunc` 以并行方式估计梯度。设置为默认值 `false` 将禁用此功能。`trust-region` 要求目标中有梯度，因此 `UseParallel` 不适用。请参阅并行计算。

示例: options = optimoptions('fminunc','SpecifyObjectiveGradient',true)

`problem` — 问题结构体
结构体

问题结构体，指定为含有以下字段的结构体：

字段名称	条目
`objective`	目标函数
`x0`	`x` 的初始点
`solver`	`'fminunc'`
`options`	用 `optimoptions` 创建的选项

数据类型: struct

输出参量

全部折叠

`x` — 解
实数向量 | 实数数组

解，以实数向量或实数数组形式返回。x 的大小与 x0 的大小相同。通常情况下，当 exitflag 为正时，x 是该问题的局部解。有关解质量的信息，请参阅求解成功后。

`fval` — 解处的目标函数值
实数

解处的目标函数值，以实数形式返回。通常，fval = fun(x)。

`exitflag` — `fminunc` 停止的原因
整数

fminunc 停止的原因，以整数形式返回。

`1`	梯度的模小于 `OptimalityTolerance` 容差。
`2`	`x` 的变化小于 `StepTolerance` 容差。
`3`	目标函数值的变化小于 `FunctionTolerance` 容差。
`5`	目标函数的预测下降小于 `FunctionTolerance` 容差。
`0`	迭代次数超出 `MaxIterations` 或函数计算次数超过 `MaxFunctionEvaluations`。
`-1`	算法已被输出函数终止。
`-3`	当前迭代的目标函数低于 `ObjectiveLimit`。

`output` — 有关优化过程的信息
结构体

有关优化过程的信息，以包含下列字段的结构体形式返回：

`iterations`	执行的迭代次数
`funcCount`	函数计算次数
`firstorderopt`	一阶最优性的测度
`algorithm`	使用的优化算法
`cgiterations`	PCG 迭代总数（仅适用于 `'trust-region'` 算法）
`lssteplength`	相对于搜索方向的线搜索步的步长（仅适用于 `'quasi-newton'` 算法）
`stepsize`	`x` 中的最终位移
`message`	退出消息

`grad` — 解处的梯度
实数向量

解处的梯度，以实数向量形式返回。grad 给出 fun 在 x(:) 点处的梯度。

`hessian` — 逼近黑塞矩阵
实矩阵

逼近黑塞矩阵，以实矩阵形式返回。有关 hessian 的含义，请参阅黑塞矩阵输出。

如果 HessianApproximation 选项是 "lbfgs" 或 {"lbfgs" n}，则返回的 hessian 是 []。

数据类型: double

详细信息

全部折叠

增强版退出消息

接下来的几项列出了可能增强的退出消息 fminunc。增强的退出消息在消息的第一句中给出了详细信息的链接。

找到局部最小值

求解器找到一个点，它似乎是局部最小值，因为一阶最优性测度小于 OptimalityTolerance 容差。

有关如何继续的建议，请参阅求解成功后。

初始点是局部最小值

初始点似乎是一个局部最小值，因为一阶最优性测度小于 OptimalityTolerance 容差。

有关如何继续的建议，请参阅终点等于初始点。

可能是局部最小值

求解器可能已经达到了局部最小值，但不能确定，因为一阶最优性测度不小于 OptimalityTolerance 容差。

有关如何继续的建议，请参阅可能是局部最小值。

求解器过早停止

求解器停止，因为它在将目标函数最小化至要求的容差之前达到了迭代或函数计算次数的限制。

有关如何继续的建议，请参阅迭代或函数计算次数太多。

问题似乎是无界问题

求解器到达一个可行点，其目标函数值小于或等于 ObjectiveLimit 容差。问题是无界的，或缩放不当，或 ObjectiveLimit 选项太高。

有关如何继续的建议，请参阅问题无界。

冲突

'trust-region' 算法要求您在目标函数中提供梯度，并将 SpecifyObjectiveGradient 选项设置为 true。

要继续，请执行以下操作之一：

将 Algorithm 选项设置为 'quasi-newton'。
确保您的目标函数提供梯度并将 SpecifyObjectiveGradient 选项设置为 true。请参阅包括梯度和黑塞函数。

退出消息的定义

接下来的几项包含以下术语的定义 fminunc 退出消息。

容差

一般来说，容差是一个阈值，超过阈值时将终止求解器的迭代。有关容差的详细信息，请参阅容差和停止条件。

局部最小值

函数的局部最小值是指这样的一个点：其函数值小于附近的点，但可能大于远处的点。

全局最小值是函数值小于所有其他可行点的点。

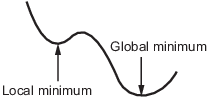
Local vs. global minimum

求解器尝试找到局部最小值。该结果也可能是全局最小值。有关详细信息，请参阅局部最优与全局最优。

一阶最优性测度

一阶最优性测度是梯度向量分量绝对值的最大值（也称为梯度的无穷范数）。在最小化点处，此值应为零。

有关详细信息，请参阅一阶最优性测度。

梯度大小

梯度大小是梯度向量分量绝对值的最大值（也称为无穷范数）。在最小化点处，此值应为零。

有关详细信息，请参阅一阶最优性测度。

`OptimalityTolerance`

称为 OptimalityTolerance 的容差与一阶最优性测度相关。当一阶最优性测度小于 OptimalityTolerance 时，迭代结束。

无约束问题的一阶最优性测度是梯度向量分量绝对值的最大值（也称为梯度的无穷范数）。在最小化点处，此值应为零。

有关详细信息，请参阅一阶最优性测度。

`FunctionTolerance`

FunctionTolerance 是一个容差为目标函数值最新变化的大小。

`StepTolerance`

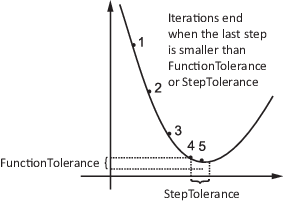
StepTolerance 是一个容差表示最后一步的大小，即评估目标函数的位置变化的大小。

当前步长的范数

当前步长的范数是计算目标函数时的位置的变化大小。

有关详细信息，请参阅容差和停止条件。

目标限值

求解器到达一个可行点，其目标函数值小于或等于 ObjectiveLimit 容差。问题是无界的，或缩放不当，或 ObjectiveLimit 选项太高。

有关如何继续的建议，请参阅问题无界。

线搜索区间

线搜索区间是沿搜索方向的线段，求解器尝试在该线段上最小化目标函数。如果此区间太小，求解器将退出。求解器根据无约束非线性优化算法中所述的各种算法计算搜索方向和此区间的大小。

输出函数或绘图函数

求解器的每次迭代都会对输出函数（或绘图函数）进行一次计算。它可以在求解器的运行过程中报告许多优化量，并可以停止求解器的运行。

有关详细信息，请参阅Optimization Toolbox 的输出函数或绘图函数。

`MaxIterations`

MaxIterations 是关于求解器执行的迭代次数的容差。当求解器执行 MaxIterations 次迭代后，迭代结束。

有关详细信息，请参阅迭代和函数计算次数或容差和停止条件。

`s`

MaxFunctionEvaluations 是关于求解器计算目标和/或约束函数的点数的容差。当求解器在 MaxFunctionEvaluations 个点上计算函数后，迭代结束。

有关详细信息，请参阅迭代和函数计算次数或容差和停止条件。

搜索方向

搜索方向是从当前点开始的向量，求解器沿该向量寻找改进。Optimization Toolbox™ 求解器通过各种算法计算搜索方向，如无约束非线性优化算法中所述。

算法

全部折叠

拟牛顿算法

默认情况下，quasi-newton 算法使用具有三次线搜索过程的 BFGS 拟牛顿法。这种拟牛顿法使用 BFGS（[1]、[5]、[8] 和 [9]）公式来更新黑塞矩阵的逼近。您还可以将低内存 BFGS 算法 ("lbfgs") 指定为 HessianApproximation 选项。您可以通过将选项设置为 'dfp' 来指定逼近逆黑塞矩阵的 DFP（[4]、[6] 和 [7]）公式，但不推荐这种做法。您可以通过将选项设置为 'steepdesc' 来指定最陡下降法，尽管此设置通常效率不高。请参阅fminunc quasi-newton 算法。

信赖域算法

trust-region 算法要求您在 fun 中提供梯度，并使用 optimoptions 将 SpecifyObjectiveGradient 设置为 true。此算法是一种子空间信赖域方法，基于 [2] 和 [3] 中所述的内部反射牛顿法。每次迭代都涉及使用预条件共轭梯度法 (PCG) 来近似求解大型线性系统。请参阅fminunc trust-region 算法、非线性最小化信赖域方法和预条件共轭梯度法。

替代功能

App

优化实时编辑器任务为 fminunc 提供了一个可视化界面。

参考

[1] Broyden, C. G. “The Convergence of a Class of Double-Rank Minimization Algorithms.” Journal Inst. Math. Applic., Vol. 6, 1970, pp. 76–90.

[2] Coleman, T. F. and Y. Li. “An Interior, Trust Region Approach for Nonlinear Minimization Subject to Bounds.” SIAM Journal on Optimization, Vol. 6, 1996, pp. 418–445.

[3] Coleman, T. F. and Y. Li. “On the Convergence of Reflective Newton Methods for Large-Scale Nonlinear Minimization Subject to Bounds.” Mathematical Programming, Vol. 67, Number 2, 1994, pp. 189–224.

[4] Davidon, W. C. “Variable Metric Method for Minimization.” A.E.C. Research and Development Report, ANL-5990, 1959.

[5] Fletcher, R. “A New Approach to Variable Metric Algorithms.” Computer Journal, Vol. 13, 1970, pp. 317–322.

[6] Fletcher, R. “Practical Methods of Optimization.” Vol. 1, Unconstrained Optimization, John Wiley and Sons, 1980.

[7] Fletcher, R. and M. J. D. Powell. “A Rapidly Convergent Descent Method for Minimization.” Computer Journal, Vol. 6, 1963, pp. 163–168.

[8] Goldfarb, D. “A Family of Variable Metric Updates Derived by Variational Means.” Mathematics of Computing, Vol. 24, 1970, pp. 23–26.

[9] Shanno, D. F. “Conditioning of Quasi-Newton Methods for Function Minimization.” Mathematics of Computing, Vol. 24, 1970, pp. 647–656.

扩展功能

全部展开

自动并行支持
通过使用 Parallel Computing Toolbox™ 自动运行并行计算来加快代码执行。

要并行运行，请将 'UseParallel' 选项设置为 true。

options = optimoptions('solvername','UseParallel',true)

有关详细信息，请参阅在 Optimization Toolbox 中使用并行计算。

版本历史记录

在 R2006a 之前推出

全部展开

R2023b: `CheckGradients` 选项将被删除

以后的版本中将会删除 CheckGradients 选项。要检查目标函数或非线性约束函数的一阶导数，请使用 checkGradients 函数。

另请参阅

fmincon | fminsearch | optimoptions | 优化

fminunc

语法

说明

示例

最小化多项式

提供梯度

使用问题结构体

获得最佳目标函数值

检查求解过程

使用 "lbfgs" 黑塞矩阵逼近求解大型问题

输入参数

fun — 最小化的函数 函数句柄 | 函数名称

x0 — 初始点 实数向量 | 实数数组

options — 优化选项 optimoptions 的输出 | 结构体，例如 optimset 返回的结构体

problem — 问题结构体 结构体

输出参量

x — 解 实数向量 | 实数数组

fval — 解处的目标函数值 实数

exitflag — fminunc 停止的原因 整数

output — 有关优化过程的信息 结构体

grad — 解处的梯度 实数向量

hessian — 逼近黑塞矩阵 实矩阵

详细信息

增强版退出消息

找到局部最小值

初始点是局部最小值

可能是局部最小值

求解器过早停止

问题似乎是无界问题

冲突

退出消息的定义

容差

局部最小值

一阶最优性测度

梯度大小

OptimalityTolerance

FunctionTolerance

StepTolerance

当前步长的范数

目标限值

线搜索区间

输出函数或绘图函数

MaxIterations

s

搜索方向

算法

拟牛顿算法

信赖域算法

替代功能

App

参考

扩展功能

自动并行支持 通过使用 Parallel Computing Toolbox™ 自动运行并行计算来加快代码执行。

版本历史记录

R2023b: CheckGradients 选项将被删除

另请参阅

主题

使用 `"lbfgs"` 黑塞矩阵逼近求解大型问题

`fun` — 最小化的函数
函数句柄 | 函数名称

`x0` — 初始点
实数向量 | 实数数组

`options` — 优化选项
`optimoptions` 的输出 | 结构体，例如 `optimset` 返回的结构体

`problem` — 问题结构体
结构体

`x` — 解
实数向量 | 实数数组

`fval` — 解处的目标函数值
实数

`exitflag` — `fminunc` 停止的原因
整数

`output` — 有关优化过程的信息
结构体

`grad` — 解处的梯度
实数向量

`hessian` — 逼近黑塞矩阵
实矩阵

`OptimalityTolerance`

`FunctionTolerance`

`StepTolerance`

`MaxIterations`

`s`

自动并行支持
通过使用 Parallel Computing Toolbox™ 自动运行并行计算来加快代码执行。

R2023b: `CheckGradients` 选项将被删除