香蕉函数的最小化
此示例说明如何最小化罗森布罗克的“香蕉函数”:
称为香蕉函数,因为它围绕原点呈弯曲状。它是优化问题中的难题,因为大多数方法在尝试求解此问题时收敛速度慢。
在 点处有唯一最小值,其中 。此示例说明从 点处开始最小化 的多种方式。
不使用导数的优化
fminsearch 函数在无约束下求问题的最小值。它使用的算法不估计目标函数的任何导数。它使用 fminsearch 算法 中所述的几何搜索方法。
使用 fminsearch 最小化香蕉函数。同时使用一个输出函数来报告迭代序列。
fun = @(x)(100*(x(2) - x(1)^2)^2 + (1 - x(1))^2); options = optimset('OutputFcn',@bananaout,'Display','off'); x0 = [-1.9,2]; [x,fval,eflag,output] = fminsearch(fun,x0,options); title 'Rosenbrock solution via fminsearch'
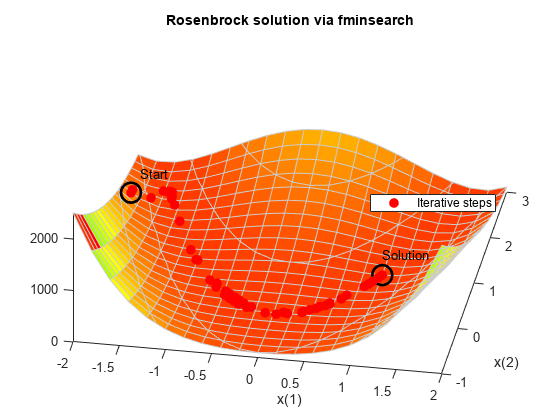
Fcount = output.funcCount;
disp(['Number of function evaluations for fminsearch was ',num2str(Fcount)])Number of function evaluations for fminsearch was 210
disp(['Number of solver iterations for fminsearch was ',num2str(output.iterations)])Number of solver iterations for fminsearch was 114
使用估计导数的优化
fminunc 函数在无约束下求问题的最小值。它使用基于导数的算法。该算法不仅尝试估计目标函数的一阶导数,还尝试估计二阶导数的矩阵。fminunc 通常比 fminsearch 效率更高。
使用 fminunc 最小化香蕉函数。
options = optimoptions('fminunc','Display','off',... 'OutputFcn',@bananaout,'Algorithm','quasi-newton'); [x,fval,eflag,output] = fminunc(fun,x0,options); title 'Rosenbrock solution via fminunc'

Fcount = output.funcCount;
disp(['Number of function evaluations for fminunc was ',num2str(Fcount)])Number of function evaluations for fminunc was 150
disp(['Number of solver iterations for fminunc was ',num2str(output.iterations)])Number of solver iterations for fminunc was 34
使用最陡下降法的优化
如果您尝试使用最陡下降算法最小化香蕉函数,问题的高曲率会使求解过程非常缓慢。
通过将 'quasi-newton' 算法的隐藏 HessUpdate 选项设置为值 'steepdesc',您可以使用最陡下降算法运行 fminunc。设置一个大于默认值的最大函数计算次数值,因为求解器无法快速找到解。在本例中,即使经过 600 次函数计算,求解器也找不到解。
options = optimoptions(options,'HessUpdate','steepdesc',... 'MaxFunctionEvaluations',600); [x,fval,eflag,output] = fminunc(fun,x0,options); title 'Rosenbrock solution via steepest descent'
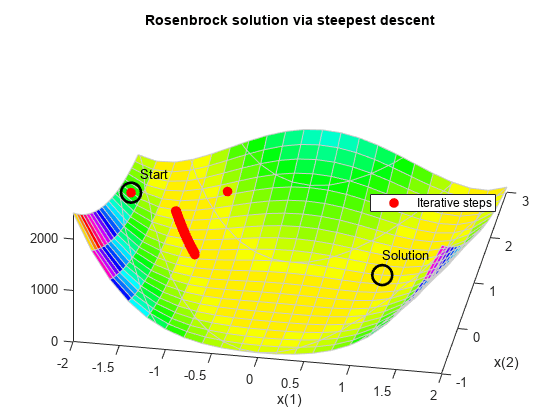
Fcount = output.funcCount; disp(['Number of function evaluations for steepest descent was ',... num2str(Fcount)])
Number of function evaluations for steepest descent was 600
disp(['Number of solver iterations for steepest descent was ',... num2str(output.iterations)])
Number of solver iterations for steepest descent was 45
使用解析梯度的优化
如果您提供梯度,fminunc 将使用更少的函数计算次数来求解优化。当您提供梯度时,您可以使用 'trust-region' 算法,该算法通常比 'quasi-newton' 算法速度更快,占用的内存更少。将 HessUpdate 和 MaxFunctionEvaluations 选项重置为其默认值。
grad = @(x)[-400*(x(2) - x(1)^2)*x(1) - 2*(1 - x(1));
200*(x(2) - x(1)^2)];
fungrad = @(x)deal(fun(x),grad(x));
options = resetoptions(options,{'HessUpdate','MaxFunctionEvaluations'});
options = optimoptions(options,'SpecifyObjectiveGradient',true,...
'Algorithm','trust-region');
[x,fval,eflag,output] = fminunc(fungrad,x0,options);
title 'Rosenbrock solution via fminunc with gradient'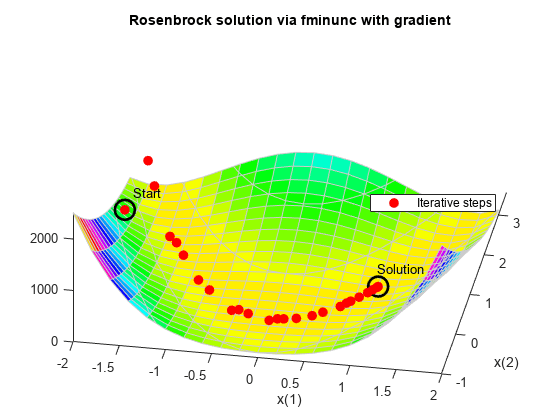
Fcount = output.funcCount; disp(['Number of function evaluations for fminunc with gradient was ',... num2str(Fcount)])
Number of function evaluations for fminunc with gradient was 32
disp(['Number of solver iterations for fminunc with gradient was ',... num2str(output.iterations)])
Number of solver iterations for fminunc with gradient was 31
使用解析黑塞矩阵的优化
如果您提供黑塞矩阵(二阶导数矩阵),fminunc 可以使用更少的函数计算次数来求解优化。对于此问题,不管是否有黑塞矩阵,结果均一样。
hess = @(x)[1200*x(1)^2 - 400*x(2) + 2, -400*x(1);
-400*x(1), 200];
fungradhess = @(x)deal(fun(x),grad(x),hess(x));
options.HessianFcn = 'objective';
[x,fval,eflag,output] = fminunc(fungradhess,x0,options);
title 'Rosenbrock solution via fminunc with Hessian'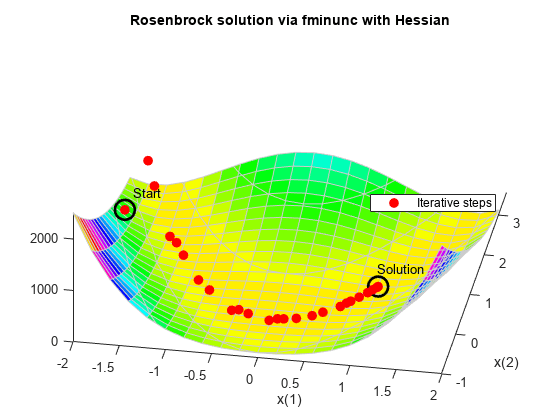
Fcount = output.funcCount; disp(['Number of function evaluations for fminunc with gradient and Hessian was ',... num2str(Fcount)])
Number of function evaluations for fminunc with gradient and Hessian was 32
disp(['Number of solver iterations for fminunc with gradient and Hessian was ',num2str(output.iterations)])Number of solver iterations for fminunc with gradient and Hessian was 31
使用最小二乘求解器的优化
非线性平方和问题的推荐求解器是 lsqnonlin。对于这类特殊问题,此求解器甚至比没有梯度的 fminunc 效率更高。要使用 lsqnonlin,请不要将您的目标写为平方和形式。而应写为可在 lsqnonlin 内用来计算平方和的基础向量。
options = optimoptions('lsqnonlin','Display','off','OutputFcn',@bananaout); vfun = @(x)[10*(x(2) - x(1)^2),1 - x(1)]; [x,resnorm,residual,eflag,output] = lsqnonlin(vfun,x0,[],[],options); title 'Rosenbrock solution via lsqnonlin'

Fcount = output.funcCount; disp(['Number of function evaluations for lsqnonlin was ',... num2str(Fcount)])
Number of function evaluations for lsqnonlin was 87
disp(['Number of solver iterations for lsqnonlin was ',num2str(output.iterations)])Number of solver iterations for lsqnonlin was 28
使用最小二乘求解器的优化和雅可比矩阵
与在 fminunc 中使用梯度进行最小化一样,lsqnonlin 可以使用导数信息来减少函数计算的次数。提供非线性目标函数向量的雅可比矩阵,并再次运行优化。
jac = @(x)[-20*x(1),10;
-1,0];
vfunjac = @(x)deal(vfun(x),jac(x));
options.SpecifyObjectiveGradient = true;
[x,resnorm,residual,eflag,output] = lsqnonlin(vfunjac,x0,[],[],options);
title 'Rosenbrock solution via lsqnonlin with Jacobian'
Fcount = output.funcCount; disp(['Number of function evaluations for lsqnonlin with Jacobian was ',... num2str(Fcount)])
Number of function evaluations for lsqnonlin with Jacobian was 29
disp(['Number of solver iterations for lsqnonlin with Jacobian was ',... num2str(output.iterations)])
Number of solver iterations for lsqnonlin with Jacobian was 28
Copyright 2006–2020 The MathWorks, Inc.