使用 Symbolic Math Toolbox 计算梯度和 Hessian

此示例使用:

此示例显示如何使用 fmincon 和 Symbolic Math Toolbox ™ 函数获得更快、更稳健的非线性优化问题解。如果您有 Symbolic Math Toolbox 许可证，您可以使用这些 Symbolic Math Toolbox 函数轻松计算目标和约束函数的解析梯度和 Hessians：

jacobian (Symbolic Math Toolbox) 生成标量函数的梯度，并生成向量函数的偏导数矩阵。因此，例如，您可以通过将 jacobian 应用于梯度来获得 Hessian 矩阵（目标函数的二阶导数）。此示例展示如何使用 jacobian 生成目标和约束函数的符号梯度和 Hessian。
matlabFunction (Symbolic Math Toolbox) 生成一个匿名函数或一个计算符号表达式的值的文件。此示例显示如何使用 matlabFunction 生成评估任意点处的目标和约束函数及其导数的文件。

Symbolic Math Toolbox 函数与 Optimization Toolbox ™ 函数相比具有不同的语法和结构。具体来说，符号变量是实数或复数标量，而 Optimization Toolbox 函数传递向量参量。因此，您需要采取几个步骤来以适合 fmincon 内点算法的形式符号化生成目标函数、约束及其所有必要的导数。

基于问题的优化可以自动计算并使用梯度；请参阅Optimization Toolbox 中的自动微分。有关使用自动微分求解该问题的基于问题的方法，请参阅使用优化变量的约束静电非线性优化。

问题描述

考虑将 10 个电子放置在导体中的静电问题。电子以最小化其总势能的方式排列，但受到位于体内的约束。所有电子至少都在物体的边界上。电子是无法区分的，因此该问题不存在唯一的最小值（在一个解中排列电子会给出另一个有效的解）。此示例受到 Dolan、Moré 和 Munson [58] 的启发。

此示例是由不等式定义的导体

$z \leq - | x | - | y |$

$x^{2} + y^{2} + (z + 1)^{2} \leq 1$ .

这个身体看上去就像球体上的一个金字塔。

[X,Y] = meshgrid(-1:.01:1);
Z1 = -abs(X) - abs(Y);
Z2 = -1 - sqrt(1 - X.^2 - Y.^2);
Z2 = real(Z2);
W1 = Z1; W2 = Z2;
W1(Z1 < Z2) = nan; % Only plot points where Z1 > Z2
W2(Z1 < Z2) = nan; % Only plot points where Z1 > Z2
hand = figure; % Handle to the figure, for more plotting later
set(gcf,'Color','w') % White background
surf(X,Y,W1,'LineStyle','none');
hold on
surf(X,Y,W2,'LineStyle','none');
view(-44,18)

图形的上下表面之间存在微小的间隙。这个间隙是用于创建图形的一般绘图程序的产物。该程序将擦除一个表面上与另一个表面接触的任何矩形斑块。

创建变量

生成一个符号向量 x，作为由实数符号变量 xij 组成的 30×1 向量，其中 i 介于 1 和 10 之间，j 介于 1 和 3 之间。这些变量代表电子 i 的三个坐标：xi1 对应 $x$ 坐标，xi2 对应 $y$ 坐标，xi3 对应 $z$ 坐标。

x = cell(3, 10);
for i = 1:10
    for j = 1:3
        x{j,i} = sprintf('x%d%d',i,j);
    end
end
x = x(:); % Now x is a 30-by-1 vector
x = sym(x, 'real');

显示向量 x。

x = 
 $(\begin{array}{c} x_{11} \\ x_{12} \\ x_{13} \\ x_{21} \\ x_{22} \\ x_{23} \\ x_{31} \\ x_{32} \\ x_{33} \\ x_{41} \\ x_{42} \\ x_{43} \\ x_{51} \\ x_{52} \\ x_{53} \\ x_{61} \\ x_{62} \\ x_{63} \\ x_{71} \\ x_{72} \\ x_{73} \\ x_{81} \\ x_{82} \\ x_{83} \\ x_{91} \\ x_{92} \\ x_{93} \\ x_{101} \\ x_{102} \\ x_{103} \end{array})$

包括线性约束

编写线性约束

$z \leq - | x | - | y |$

对于每个电子，有一组四个线性不等式：

xi3 - xi1 - xi2 ≤ 0
xi3 - xi1 + xi2 ≤ 0
xi3 + xi1 - xi2 ≤ 0
xi3 + xi1 + xi2 ≤ 0

所以，这道题总共有 40 个线性不等式。

以结构化的方式写出不等式。

B = [1,1,1;-1,1,1;1,-1,1;-1,-1,1];

A = zeros(40,30);
for i=1:10
    A(4*i-3:4*i,3*i-2:3*i) = B;
end

b = zeros(40,1);

您可以看到 A*x ≤ b 代表不等式。

disp(A*x)

 $(\begin{array}{c} x_{11} + x_{12} + x_{13} \\ x_{12} - x_{11} + x_{13} \\ x_{11} - x_{12} + x_{13} \\ x_{13} - x_{12} - x_{11} \\ x_{21} + x_{22} + x_{23} \\ x_{22} - x_{21} + x_{23} \\ x_{21} - x_{22} + x_{23} \\ x_{23} - x_{22} - x_{21} \\ x_{31} + x_{32} + x_{33} \\ x_{32} - x_{31} + x_{33} \\ x_{31} - x_{32} + x_{33} \\ x_{33} - x_{32} - x_{31} \\ x_{41} + x_{42} + x_{43} \\ x_{42} - x_{41} + x_{43} \\ x_{41} - x_{42} + x_{43} \\ x_{43} - x_{42} - x_{41} \\ x_{51} + x_{52} + x_{53} \\ x_{52} - x_{51} + x_{53} \\ x_{51} - x_{52} + x_{53} \\ x_{53} - x_{52} - x_{51} \\ x_{61} + x_{62} + x_{63} \\ x_{62} - x_{61} + x_{63} \\ x_{61} - x_{62} + x_{63} \\ x_{63} - x_{62} - x_{61} \\ x_{71} + x_{72} + x_{73} \\ x_{72} - x_{71} + x_{73} \\ x_{71} - x_{72} + x_{73} \\ x_{73} - x_{72} - x_{71} \\ x_{81} + x_{82} + x_{83} \\ x_{82} - x_{81} + x_{83} \\ x_{81} - x_{82} + x_{83} \\ x_{83} - x_{82} - x_{81} \\ x_{91} + x_{92} + x_{93} \\ x_{92} - x_{91} + x_{93} \\ x_{91} - x_{92} + x_{93} \\ x_{93} - x_{92} - x_{91} \\ x_{101} + x_{102} + x_{103} \\ x_{102} - x_{101} + x_{103} \\ x_{101} - x_{102} + x_{103} \\ x_{103} - x_{102} - x_{101} \end{array})$

创建非线性约束及其梯度和 Hessian

非线性约束也是结构化的。

$x^{2} + y^{2} + (z + 1)^{2} \leq 1$ .

生成约束及其梯度和 Hessian。

c = sym(zeros(1,10));
i = 1:10;
c = (x(3*i-2).^2 + x(3*i-1).^2 + (x(3*i)+1).^2 - 1).';

gradc = jacobian(c,x).'; % .' performs transpose

hessc = cell(1, 10);
for i = 1:10
    hessc{i} = jacobian(gradc(:,i),x);
end

约束向量 c 是行向量， c(i) 的梯度表示在矩阵 gradc 的第 i 列。这种形式是正确的，如非线性约束所述。

Hessian 矩阵 hessc{1}、...、hessc{10} 是方阵且对称。此示例将它们存储在元胞数组中，这比将它们存储在单独的变量（例如 hessc1, ..., hessc10 ）中更好。

使用 .' 语法进行转置。' 语法表示共轭转置，它具有不同的符号导数。

创建目标函数及其梯度和 Hessian

目标函数，势能，是每个电子对之间距离的倒数的总和。

$e n e r g y = \sum_{i < j} \frac{1}{| x_{i} - x_{j} |}$ .

距离是向量各个分量之差的平方和的平方根。

计算能量（目标函数）及其梯度和 Hessian。

energy = sym(0);
for i = 1:3:25
    for j = i+3:3:28
        dist = x(i:i+2) - x(j:j+2);
        energy = energy + 1/sqrt(dist.'*dist);
    end
end

gradenergy = jacobian(energy,x).';

hessenergy = jacobian(gradenergy,x);

创建目标函数文件

目标函数有两个输出，energy 和 gradenergy。调用 matlabFunction 时将两个函数放在一个向量中，以减少 matlabFunction 生成的子表达式的数量，并且仅当调用函数（在本例中为 fmincon）请求两个输出时才返回梯度。您可以将生成的文件放在 MATLAB 路径上的任何文件夹中。在这种情况下，将它们放在当前文件夹中。

currdir = [pwd filesep]; % You might need to use currdir = pwd 
filename = [currdir,'demoenergy.m'];
matlabFunction(energy,gradenergy,'file',filename,'vars',{x});

matlabFunction 返回 energy 作为第一个输出，返回 gradenergy 作为第二个输出。该函数还采用单个输入向量 {x} ，而不是输入列表 x11, ..., x103。

生成的文件 demoenergy.m 包含以下行或类似内容：

function [energy,gradenergy] = demoenergy(in1)
%DEMOENERGY
%   [ENERGY,GRADENERGY] = DEMOENERGY(IN1)
...
x101 = in1(28,:);
...
energy = 1./t140.^(1./2) + ...;
if nargout > 1
    ...
    gradenergy = [(t174.*(t185 - 2.*x11))./2 - ...];
end

此函数具有带梯度的目标函数的正确形式；请参阅编写标量目标函数。

创建约束函数文件

生成非线性约束函数，并将其置于正确的格式。

filename = [currdir,'democonstr.m'];
matlabFunction(c,[],gradc,[],'file',filename,'vars',{x},...
    'outputs',{'c','ceq','gradc','gradceq'});

生成的文件 democonstr.m 包含以下行或类似内容：

function [c,ceq,gradc,gradceq] = democonstr(in1)
%DEMOCONSTR
%    [C,CEQ,GRADC,GRADCEQ] = DEMOCONSTR(IN1)
...
x101 = in1(28,:);
...
c = [t417.^2 + ...];
if nargout > 1
    ceq = [];
end
if nargout > 2
    gradc = [2.*x11,...];
end
if nargout > 3
    gradceq = [];
end

此函数具有带梯度的约束函数的正确形式；请参阅非线性约束。

生成 Hessian 文件

为了生成该问题的拉格朗日 Hessian，首先生成能量 Hessian 和约束 Hessian 文件。

目标函数的 Hessian 矩阵 hessenergy 是一个包含超过 150,000 个符号的大型符号表达式，如评估 size(char(hessenergy)) 所示。因此，运行 matlabFunction(hessenergy) 需要大量时间。

生成文件 hessenergy.m。

filename = [currdir,'hessenergy.m'];
matlabFunction(hessenergy,'file',filename,'vars',{x});

相比之下，约束函数的 Hessian 很小，计算速度很快。

for i = 1:10
    ii = num2str(i);
    thename = ['hessc',ii];
    filename = [currdir,thename,'.m'];
    matlabFunction(hessc{i},'file',filename,'vars',{x});
end

生成目标和约束的所有文件后，将它们与辅助函数 hessfinal.m 中的相应拉格朗日乘数一起放入其中，该函数的代码出现在本示例的末尾。

运行优化

从以 [0,0,-1] 为中心、半径为 1/2 的球体上随机分布的电子开始优化。

rng default % For reproducibility
Xinitial = randn(3,10); % Columns are normal 3-D vectors
for j=1:10
    Xinitial(:,j) = Xinitial(:,j)/norm(Xinitial(:,j))/2;
    % This normalizes to a 1/2-sphere
end
Xinitial(3,:) = Xinitial(3,:) - 1; % Center at [0,0,-1]
Xinitial = Xinitial(:); % Convert to a column vector

设置选项以使用 interior-point 算法，并使用梯度和 Hessian。

options = optimoptions(@fmincon,'Algorithm','interior-point','SpecifyObjectiveGradient',true,...
    'SpecifyConstraintGradient',true,'HessianFcn',@hessfinal,'Display','final');

调用 fmincon。

[xfinal,fval,exitflag,output] = fmincon(@demoenergy,Xinitial,...
    A,b,[],[],[],[],@democonstr,options);

Local minimum found that satisfies the constraints.

Optimization completed because the objective function is non-decreasing in 
feasible directions, to within the value of the optimality tolerance,
and constraints are satisfied to within the value of the constraint tolerance.

<stopping criteria details>

查看目标函数值、退出标志、迭代次数和函数计算次数。

disp(fval)

   34.1365

disp(exitflag)

disp(output.iterations)

disp(output.funcCount)

尽管电子的初始位置是随机的，但最终位置几乎是对称的。

for i = 1:10
    plot3(xfinal(3*i-2),xfinal(3*i-1),xfinal(3*i),'r.','MarkerSize',25);
end

要检查整个 3-D 几何形状，请旋转图形。

rotate3d

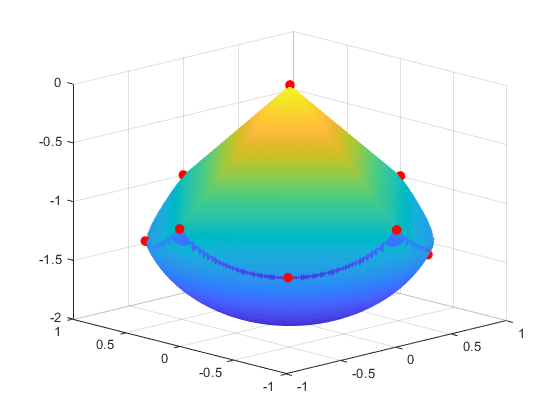
figure(hand)

与不使用梯度和 Hessian 的优化进行比较

梯度和 Hessians 的使用使得优化运行得更快、更准确。为了比较不使用梯度或 Hessian 信息的相同优化，请将选项设置为不使用梯度和 Hessian。

options = optimoptions(@fmincon,'Algorithm','interior-point',...
    'Display','final');
[xfinal2,fval2,exitflag2,output2] = fmincon(@demoenergy,Xinitial,...
    A,b,[],[],[],[],@democonstr,options);

Feasible point with lower objective function value found.


Local minimum found that satisfies the constraints.

Optimization completed because the objective function is non-decreasing in 
feasible directions, to within the value of the optimality tolerance,
and constraints are satisfied to within the value of the constraint tolerance.

<stopping criteria details>

查看目标函数值、退出标志、迭代次数和函数计算次数。

disp(fval2)

   34.1365

disp(exitflag2)

disp(output2.iterations)

disp(output2.funcCount)

比较有和没有导数信息的迭代次数和函数计算次数。

tbl = table([output.iterations;output2.iterations],[output.funcCount;output2.funcCount],...
    'RowNames',{'With Derivatives','Without Derivatives'},'VariableNames',{'Iterations','Fevals'})

tbl=2×2 table
                           Iterations    Fevals
                           __________    ______

    With Derivatives           19           28 
    Without Derivatives        77         2434

清除符号变量假设

本例中的符号变量假设它们在符号引擎工作区中是真实的。删除变量并不会从符号引擎工作区中清除这个假设。使用 syms 清除变量假设。

syms x

验证假设是否为空。

assumptions(x)

 
ans =
 
Empty sym: 1-by-0

辅助函数

以下代码创建 hessfinal 辅助函数。

function H = hessfinal(X,lambda)
%
% Call the function hessenergy to start
H = hessenergy(X);

% Add the Lagrange multipliers * the constraint Hessians
H = H + hessc1(X) * lambda.ineqnonlin(1);
H = H + hessc2(X) * lambda.ineqnonlin(2);
H = H + hessc3(X) * lambda.ineqnonlin(3);
H = H + hessc4(X) * lambda.ineqnonlin(4);
H = H + hessc5(X) * lambda.ineqnonlin(5);
H = H + hessc6(X) * lambda.ineqnonlin(6);
H = H + hessc7(X) * lambda.ineqnonlin(7);
H = H + hessc8(X) * lambda.ineqnonlin(8);
H = H + hessc9(X) * lambda.ineqnonlin(9);
H = H + hessc10(X) * lambda.ineqnonlin(10);
end