自动微分背景

什么是自动微分？

自动微分（也称为autodiff、AD 或算法微分）是优化中广泛使用的工具。solve 函数在基于问题的优化中默认使用自动微分，适用于一般非线性目标函数和约束；请参阅 Optimization Toolbox 中的自动微分。

自动微分是一组用数值方法计算导数（梯度）的技术。该方法使用符号规则进行微分，比有限差分近似更准确。与纯符号方法不同，自动微分在计算的早期就以数值方式评估表达式，而不是执行大型符号计算。换句话说，自动微分会计算特定数值的导数；它不会为导数构建符号表达式。

正向模式自动微分通过与函数本身的求值运算同时执行基本导数运算来求出数值导数。如下一节所述，软件在计算图上执行这些计算。
反向模式自动微分使用正向模式计算图的扩展，使得能够通过反向遍历图来计算梯度。当软件运行代码来计算函数及其导数时，它会将操作记录在称为跟踪的数据结构中。

正如许多研究人员所指出的（例如，Baydin、Pearlmutter、Radul 和 Siskind [1]），对于许多变量的标量函数，反向模式比正向模式更有效地计算梯度。由于目标函数是标量，因此 solve 自动微分使用反向模式进行标量优化。但是，对于非线性最小二乘和方程求解等矢量值函数，solve 使用正向模式进行某些计算。请参阅Optimization Toolbox 中的自动微分。

正向模式

考虑评估此函数及其梯度的问题：

$f (x) = x_{1} \exp (- \frac{1}{2} (x_{1}^{2} + x_{2}^{2})) .$

自动微分在特定点起作用。本例中，取 x₁ = 2，x₂ = 1/2。

下面的计算图对函数 f(x) 的计算进行了编码。

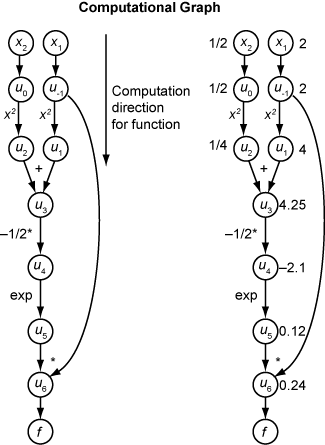
要使用正向模式计算 f(x) 的梯度，您需要在相同方向上计算相同的图，但根据微分的基本规则修改计算。为了进一步简化计算，您可以随时填写每个子表达式 u_i 的导数的值。为了计算整个梯度，必须遍历图两次，一次针对每个独立变量求偏导数。链式法则中的每个子表达式都有一个数值，因此整个表达式具有与函数本身相同类型的求值图。

计算是链式法则的重复应用。在此示例中，f 对 x₁ 的导数扩展为以下表达式：

$\begin{matrix} \frac{d f}{d x_{1}} = \frac{d u_{6}}{d x_{1}} \\ = \frac{\partial u_{6}}{\partial u_{- 1}} + \frac{\partial u_{6}}{\partial u_{5}} \frac{\partial u_{5}}{\partial x_{1}} \\ = \frac{\partial u_{6}}{\partial u_{- 1}} + \frac{\partial u_{6}}{\partial u_{5}} \frac{\partial u_{5}}{\partial u_{4}} \frac{\partial u_{4}}{\partial x_{1}} \\ = \frac{\partial u_{6}}{\partial u_{- 1}} + \frac{\partial u_{6}}{\partial u_{5}} \frac{\partial u_{5}}{\partial u_{4}} \frac{\partial u_{4}}{\partial u_{3}} \frac{\partial u_{3}}{\partial x_{1}} \\ = \frac{\partial u_{6}}{\partial u_{- 1}} + \frac{\partial u_{6}}{\partial u_{5}} \frac{\partial u_{5}}{\partial u_{4}} \frac{\partial u_{4}}{\partial u_{3}} \frac{\partial u_{3}}{\partial u_{1}} \frac{\partial u_{1}}{\partial x_{1}} . \end{matrix}$

让 ${\dot{u}}_{i}$ 表示表达式 u_i 关于 x₁ 的导数。使用函数评估中得到的 u_i 的评估值，计算 f 关于 x₁ 的偏导数，如下图所示。请注意，当您从上到下遍历图表时， ${\dot{u}}_{i}$ 的所有值均变为可用。

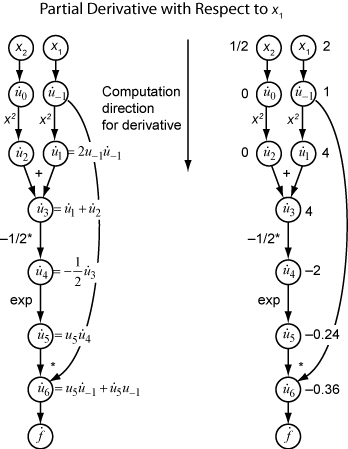
为了计算关于 x₂ 的偏导数，您需要遍历类似的计算图。因此，当计算函数的梯度时，图遍历的次数与变量的数量相同。当目标函数或非线性约束依赖于许多变量时，这个过程对于许多应用来说可能很慢。

反向模式

反向模式使用计算图的一次正向遍历来设置跟踪。然后，它在相反方向的一次图遍历中计算函数的整个梯度。对于含有许多变量的问题，这种模式效率更高。

反向模式背后的理论也是基于链式法则，以及用上划线表示的相关伴随变量。u_i 的伴随变量是

${\bar{u}}_{i} = \frac{\partial f}{\partial u_{i}} .$

就计算图而言，变量的每个传出箭头根据链式法则的项对相应的伴随变量做出贡献。例如，变量 u_–1 具有指向两个变量 u₁ 和 u₆ 的传出箭头。该图有相关方程

$\begin{matrix} \frac{\partial f}{\partial u_{- 1}} = \frac{\partial f}{\partial u_{1}} \frac{\partial u_{1}}{\partial u_{- 1}} + \frac{\partial f}{\partial u_{6}} \frac{\partial u_{6}}{\partial u_{- 1}} \\ = {\bar{u}}_{1} \frac{\partial u_{1}}{\partial u_{- 1}} + {\bar{u}}_{6} \frac{\partial u_{6}}{\partial u_{- 1}} . \end{matrix}$

在这个计算中，回想一下 $u_{1} = u_{- 1}^{2}$ 和 u₆ = u₅u_–1，您得到

${\bar{u}}_{- 1} = {\bar{u}}_{1} 2 u_{- 1} + {\bar{u}}_{6} u_{5} .$

在图的正向遍历过程中，软件计算中间变量 u_i。在反向遍历过程中，从种子值 ${\bar{u}}_{6} = \frac{\partial f}{\partial f} = 1$ 开始，反向模式计算获得所有变量的伴随值。因此，反向模式只需一次计算即可计算梯度，与正向模式相比节省了大量时间。

下图显示了该函数以反向模式计算梯度

$f (x) = x_{1} \exp (- \frac{1}{2} (x_{1}^{2} + x_{2}^{2})) .$

再次，计算需要 x₁ = 2，x₂ = 1/2。反向模式计算依赖于原始计算图中函数计算过程中获得的 u_i 值。在图的右侧部分，使用图的左侧部分的公式，伴随变量的计算值出现在伴随变量名称旁边。

最终的渐变值显示为 ${\bar{u}}_{0} = \frac{\partial f}{\partial u_{0}} = \frac{\partial f}{\partial x_{2}}$ 和 ${\bar{u}}_{- 1} = \frac{\partial f}{\partial u_{- 1}} = \frac{\partial f}{\partial x_{1}}$ 。

有关更多详细信息，请参阅 Baydin、Pearlmutter、Radul 和 Siskind [1] 或有关自动微分 [2] 的维基百科文章。

闭式解

对于线性或二次目标或约束函数，可以根据系数以非常低的计算成本明确地获得梯度。在这些情况下，solve 和 prob2struct 明确提供梯度，而无需经过 AD，并且适用的求解器始终使用梯度。如果您获得 output 结构，则相关的 objectivederivative 或 constraintderivative 字段的值为 "closed-form"。

Optimization Toolbox 中的自动微分

在以下条件下，自动微分 (AD) 适用于 solve 和 prob2struct 函数：

目标函数和约束函数受支持，如优化变量和表达式支持的运算中所述。它们不需要使用 fcn2optimexpr 函数。
solve 调用的求解器是 fmincon、fminunc、fsolve 或 lsqnonlin。
对于优化问题，solve 或 prob2struct 的 'ObjectiveDerivative' 和 'ConstraintDerivative' 名称-值对组参量设置为 'auto'（默认值）、'auto-forward' 或 'auto-reverse'。
对于方程问题，'EquationDerivative' 选项设置为 'auto'（默认值）、'auto-forward' 或 'auto-reverse'。

AD 的适用情形	所有约束函数均受支持	一个或多个约束不受支持
目标函数受支持	AD 用于目标和约束	AD 仅用于目标
目标函数不受支持	AD 仅用于约束	不使用 AD

注意

对于线性或二次目标或约束函数，适用的求解器始终使用显函数梯度。这些梯度不是使用 AD 生成的。请参阅闭式解。

当不满足这些条件时，solve 通过有限差分来估计梯度，prob2struct 不会在其生成的函数文件中创建梯度。

默认情况下，求解器选择以下 AD 类型：

对于一般的非线性目标函数，fmincon 默认选择反向 AD。对于非线性约束函数，如果其非线性约束的数量小于变量数目，fmincon 默认选择反向 AD。否则，fmincon 默认选择正向 AD。
对于一般的非线性目标函数，fminunc 默认选择反向 AD。
对于最小二乘目标函数，fmincon 和 fminunc 对目标函数默认选择正向 AD。有关基于问题的最小二乘目标函数的定义，请参阅编写基于问题的最小二乘法的目标函数。
当目标向量中的元素数大于或等于变量数时，lsqnonlin 默认选择正向 AD。否则，lsqnonlin 默认选择反向 AD。
当方程数大于或等于变量数时，fsolve 默认选择正向 AD。否则，fsolve 默认选择反向 AD。

注意

要在由 prob2struct 转换的问题中使用自动导数，请传递指定这些导数的选项。

options = optimoptions('fmincon','SpecifyObjectiveGradient',true,...
    'SpecifyConstraintGradient',true);
problem.options = options;

当前，AD 仅适用于一阶导数；它不适用于二阶或更高阶导数。因此，在某些情况下（例如，如果您要使用解析黑塞矩阵来加速优化），您无法直接使用 solve，而必须使用基于问题的工作流中的供应衍生品中所述的方法。

参考

[1] Baydin, Atilim Gunes, Barak A. Pearlmutter, Alexey Andreyevich Radul, and Jeffrey Mark Siskind. "Automatic Differentiation in Machine Learning: A Survey." The Journal of Machine Learning Research, 18(153), 2018, pp. 1–43. Available at https://arxiv.org/abs/1502.05767.

[2] Automatic differentiation. Wikipedia. Available at https://en.wikipedia.org/wiki/Automatic_differentiation.

另请参阅

solve | prob2struct