本页采用了机器翻译。点击此处可查看最新英文版本。

OptimizationValues

优化问题的值

自 R2022a 起

全页展开

说明

OptimizationValues 对象保留 solve 所使用并为多目标问题返回的值。该对象还保留接受多个起点的求解器的 x0 参量起始值。

创建对象

solve 函数返回 OptimizationValues 对象的向量作为多目标问题的解。

使用 optimvalues 函数为起点 x0 创建一个 OptimizationValues 对象。

属性

全部展开

通常，OptimizationValues 属性是动态的：它们是优化变量、目标函数和约束的名称。

但是，您也可以有未命名的目标函数或约束。对于这些情况，OptimizationValues 会对以下属性赋值。

目标函数值，以实数数组形式返回或指定。

数据类型: double

约束值，以实数数组形式返回或指定。

数据类型: double

对象函数

paretoplot多目标的帕累托图

示例

全部折叠

此示例使用:

打开实时脚本

使用优化变量创建和求解一个多目标问题。

x = optimvar("x",LowerBound=-3,UpperBound=3);
prob = optimproblem;
prob.Objective = [x^2;(x-1)^2]; % Tradeoff region between x = 0 and x = 1
prob.Constraints.con1 = x^2 <= 1/2; % Demonstrate constraints
prob.Constraints.con2 = x^2 >= 1/10; % Second constraint
rng default % For reproducibility
[sol,fval,exitflag,output] = solve(prob,Solver="paretosearch")
Solving problem using paretosearch.

Pareto set found that satisfies the constraints. 

Optimization completed because the relative change in the volume of the Pareto set 
is less than 'options.ParetoSetChangeTolerance' and constraints are satisfied to within 
'options.ConstraintTolerance'.

sol = 
  1×60 OptimizationValues vector with properties:

   Variables properties:
            x: [0.7027 0.7014 0.3635 0.3491 0.5723 0.3177 0.4634 0.4400 0.6379 0.6402 0.3750 0.6057 0.6565 0.5483 0.6455 0.5518 0.3760 0.3232 0.6768 0.6357 0.5625 0.3952 0.3382 0.3857 0.5677 0.5170 0.5107 0.6241 0.6615 0.3295 0.6875 … ] (1×60 double)

   Objective properties:
    Objective: [2×60 double]

   Constraints properties:
         con1: [-0.0063 -0.0081 -0.3679 -0.3781 -0.1725 -0.3991 -0.2853 -0.3064 -0.0931 -0.0902 -0.3594 -0.1332 -0.0690 -0.1994 -0.0833 -0.1955 -0.3586 -0.3955 -0.0420 -0.0959 -0.1836 -0.3438 -0.3856 -0.3512 -0.1777 -0.2327 -0.2392 … ] (1×60 double)
         con2: [-0.3937 -0.3919 -0.0321 -0.0219 -0.2275 -9.3572e-04 -0.1147 -0.0936 -0.3069 -0.3098 -0.0406 -0.2668 -0.3310 -0.2006 -0.3167 -0.2045 -0.0414 -0.0045 -0.3580 -0.3041 -0.2164 -0.0562 -0.0144 -0.0488 -0.2223 -0.1673 -0.1608 … ] (1×60 double)


fval = 2×60

    0.4937    0.4919    0.1321    0.1219    0.3275    0.1009    0.2147    0.1936    0.4069    0.4098    0.1406    0.3668    0.4310    0.3006    0.4167    0.3045    0.1414    0.1045    0.4580    0.4041    0.3164    0.1562    0.1144    0.1488    0.3223    0.2673    0.2608    0.3895    0.4375    0.1086    0.4727    0.2001    0.4395    0.2261    0.1658    0.4862    0.4270    0.3525    0.1057    0.2628    0.2197    0.4902    0.1760    0.3665    0.2411    0.1092    0.4911    0.1914    0.1182    0.3742
    0.0884    0.0892    0.4051    0.4237    0.1829    0.4655    0.2880    0.3136    0.1311    0.1295    0.3906    0.1555    0.1180    0.2040    0.1257    0.2009    0.3893    0.4580    0.1045    0.1327    0.1914    0.3658    0.4380    0.3773    0.1869    0.2333    0.2394    0.1413    0.1146    0.4496    0.0977    0.3055    0.1136    0.2751    0.3514    0.0916    0.1201    0.1650    0.4555    0.2375    0.2822    0.0899    0.3369    0.1557    0.2591    0.4483    0.0895    0.3164    0.4307    0.1508


exitflag = 
    SolverConvergedSuccessfully


output = struct with fields:
         iterations: 20
          funccount: 380
             volume: 1.8611
    averagedistance: 0.0101
             spread: 0.3067
      maxconstraint: 0
            message: 'Pareto set found that satisfies the constraints. ↵↵Optimization completed because the relative change in the volume of the Pareto set ↵is less than 'options.ParetoSetChangeTolerance' and constraints are satisfied to within ↵'options.ConstraintTolerance'.'
           rngstate: [1×1 struct]
             solver: 'paretosearch'

paretosearch 求解器经过 16 次迭代收敛于一个可行解。绘制解。

paretoplot(sol)

Figure contains an axes object. The axes object with title Pareto Front, xlabel Objective(1), ylabel Objective(2) contains 4 objects of type text, scatter.

使用数据提示选择图中的一个任意点进行检查：

arbitrarydatatip.png

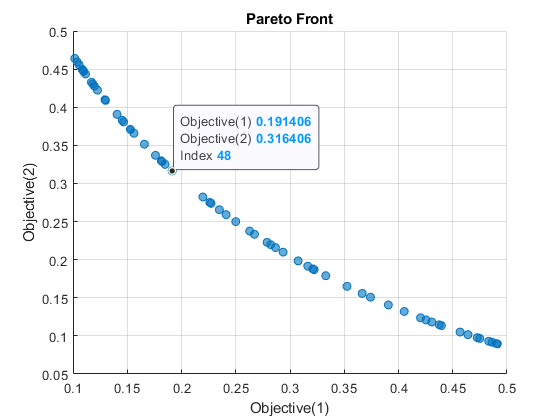
arbitrary.png

图中的点位于索引 48 处。检查解 48。

arbitrarysol = sol(48)
arbitrarysol = 
  OptimizationValues with properties:

   Variables properties:
            x: 0.4375

   Objective properties:
    Objective: [2×1 double]

   Constraints properties:
         con1: -0.3086
         con2: -0.0914

约束值为负，表示图中的点可行。

arbitrarysol.Objective
ans = 2×1

    0.1914
    0.3164

目标值与数据提示中的值匹配。

限制

  • OptimizationValues 对象仅支持水平串联。换句话说，您只能有由 OptimizationValues 对象组成的行向量。

版本历史记录

在 R2022a 中推出

另请参阅

主题