基于问题的多目标优化的帕累托前沿

此示例说明如何使用优化变量解决多目标优化问题，以及如何绘制解。

问题表示

该问题有一个二维优化变量和两个目标函数。创建优化变量 x 作为行向量，这是多目标求解器所期望的方向。设置边界，指定 x 的分量范围从 -50 到 50。

x = optimvar("x",1,2,LowerBound=-50,UpperBound=50);

创建双组分目标函数。将目标函数纳入优化问题中。

fun(1) = x(1)^4 + x(2)^4 + x(1)*x(2) - x(1)^2*x(2)^2 - 9*x(1)^2;
fun(2) = x(1)^4 + x(2)^4 + x(1)*x(2) - x(1)^2*x(2)^2 + 3*x(2)^3;
prob = optimproblem("Objective",fun);

检查此问题。

show(prob)

  OptimizationProblem : 

	Solve for:
       x

	minimize :
       ((((x(1).^4 + x(2).^4) + (x(1) .* x(2))) - (x(1).^2 .* x(2).^2)) - (9 .* x(1).^2))
       ((((x(1).^4 + x(2).^4) + (x(1) .* x(2))) - (x(1).^2 .* x(2).^2)) + (3 .* x(2).^3))


	variable bounds:
       -50 <= x(1) <= 50
       -50 <= x(2) <= 50

求解并绘制解

调用 solve 以求解问题。

rng default % For reproducibility
sol = solve(prob)

Solving problem using gamultiobj.
gamultiobj stopped because the average change in the spread of Pareto solutions is less than options.FunctionTolerance.

sol = 
  1×18 OptimizationValues vector with properties:

   Variables properties:
            x: [2×18 double]

   Objective properties:
    Objective: [2×18 double]

绘制最终的帕累托前沿。

paretoplot(sol)

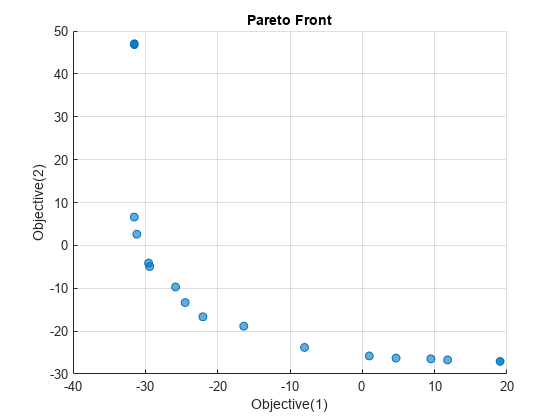
Figure contains an axes object. The axes object with title Pareto Front, xlabel Objective(1), ylabel Objective(2) contains 4 objects of type text, scatter.

使用 paretosearch 求解器再次求解该问题。

sol2 = solve(prob,Solver="paretosearch");

Solving problem using paretosearch.

Pareto set found that satisfies the constraints. 

Optimization completed because the relative change in the volume of the Pareto set 
is less than 'options.ParetoSetChangeTolerance' and constraints are satisfied to within 
'options.ConstraintTolerance'.

paretoplot(sol2)

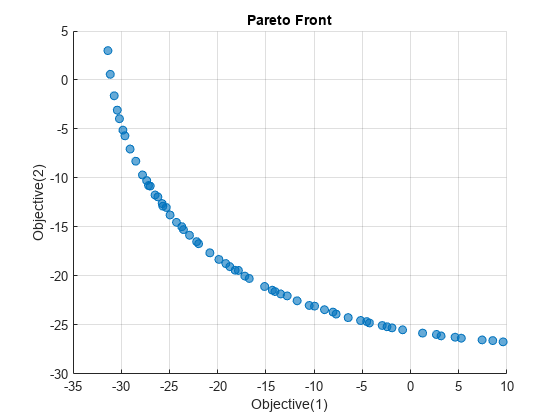
Figure contains an axes object. The axes object with title Pareto Front, xlabel Objective(1), ylabel Objective(2) contains 4 objects of type text, scatter.

使用默认选项，paretosearch 求解器会获得比 gamultiobj 更密集的解点集。但是，gamultiobj 获得了更广泛的值范围。

从单目标解开始

为了尝试实现更好的解传播，从 x = [1 1] 开始寻找单目标解。

x0.x = [1 1];
prob1 = optimproblem("Objective",fun(1));
solp1 = solve(prob1,x0);

Solving problem using fmincon.

Local minimum possible. Constraints satisfied.

fmincon stopped because the size of the current step is less than
the value of the step size tolerance and constraints are 
satisfied to within the value of the constraint tolerance.

<stopping criteria details>

prob2 = optimproblem("Objective",fun(2));
solp2 = solve(prob2,x0);

Solving problem using fmincon.

Local minimum found that satisfies the constraints.

Optimization completed because the objective function is non-decreasing in 
feasible directions, to within the value of the optimality tolerance,
and constraints are satisfied to within the value of the constraint tolerance.

<stopping criteria details>

准备单目标解作为 solve 的初始点。每个点必须作为列向量传递给 optimvalues 函数。

start = optimvalues(prob,"x",[solp1.x' solp2.x']);

从 paretosearch 点出发，解决 start 的多目标问题。

sol3 = solve(prob,start,Solver="paretosearch");

Solving problem using paretosearch.

Pareto set found that satisfies the constraints. 

Optimization completed because the relative change in the volume of the Pareto set 
is less than 'options.ParetoSetChangeTolerance' and constraints are satisfied to within 
'options.ConstraintTolerance'.

paretoplot(sol3)

Figure contains an axes object. The axes object with title Pareto Front, xlabel Objective(1), ylabel Objective(2) contains 4 objects of type text, scatter.

这次，paretosearch 发现目标函数的范围更大，在目标 2 中几乎达到 10，在目标 1 中几乎达到 20。该范围与 gamultiobj 范围相似，但目标 1 = –31、目标 2 = 48 附近的异常解点除外。

另请参阅

gamultiobj | paretosearch | solve | paretoplot

主题

多目标优化