quadprog

二次规划

全页折叠

语法

x = quadprog(H,f)

x = quadprog(H,f,A,b)

x = quadprog(H,f,A,b,Aeq,beq)

x = quadprog(H,f,A,b,Aeq,beq,lb,ub)

x = quadprog(H,f,A,b,Aeq,beq,lb,ub,x0)

x = quadprog(H,f,A,b,Aeq,beq,lb,ub,x0,options)

x = quadprog(problem)

[x,fval] = quadprog(___)

[x,fval,exitflag,output] = quadprog(___)

[x,fval,exitflag,output,lambda] = quadprog(___)

[wsout,fval,exitflag,output,lambda] = quadprog(H,f,A,b,Aeq,beq,lb,ub,ws)

说明

具有线性约束的二次目标函数的求解器。

quadprog 求由下式指定的问题的最小值

$\min_{x} \frac{1}{2} x^{T} H x + f^{T} x such that {\begin{matrix} A \cdot x \leq b, \\ A e q \cdot x = b e q, \\ l b \leq x \leq u b . \end{matrix}$

H、A 和 Aeq 是矩阵，f、b、beq、lb、ub 和 x 是向量。

您可以将 f、lb 和 ub 作为向量或矩阵进行传递；请参阅矩阵参量。

注意

quadprog 仅适用于基于求解器的方法。使用 solve 作为基于问题的方法。有关这两种优化方法的讨论，请参阅首先选择基于问题或基于求解器的方法。

x = quadprog(H,f) 返回使 1/2*x'*H*x + f'*x 最小的向量 x。要使问题具有有限最小值，输入 H 必须为正定矩阵。如果 H 是正定矩阵，则解 x = H\(-f)。

x = quadprog(H,f,A,b) 在 A*x ≤ b 的条件下最小化 1/2*x'*H*x + f'*x。输入 A 是由双精度值组成的矩阵，b 是由双精度值组成的向量。

示例

x = quadprog(H,f,A,b,Aeq,beq) 在满足 Aeq*x = beq 的限制条件下求解上述问题。Aeq 是由双精度值组成的矩阵，beq 是由双精度值组成的向量。如果不存在不等式，则设置 A = [] 和 b = []。

示例

x = quadprog(H,f,A,b,Aeq,beq,lb,ub) 在满足 lb ≤ x ≤ ub 的限制条件下求解上述问题。输入 lb 和 ub 是由双精度值组成的向量，这些限制适用于每个 x 分量。如果不存在等式，请设置 Aeq = [] 和 beq = []。

注意

如果为问题指定的输入边界不一致，则输出 x 为 x0，输出 fval 为 []。

quadprog 将 x0 中违反边界 lb ≤ x ≤ ub 的分量重置为在这些边界定义的框内。quadprog 不会更改遵守边界的分量。

示例

x = quadprog(H,f,A,b,Aeq,beq,lb,ub,x0) 从向量 x0 开始求解上述问题。如果不存在边界，请设置 lb = [] 和 ub = []。一些 quadprog 算法会忽略 x0；请参阅 x0。

注意

x0 是 'active-set' 算法的必需参量。

x = quadprog(H,f,A,b,Aeq,beq,lb,ub,x0,options) 使用 options 中指定的优化选项求解上述问题。使用 optimoptions 创建 options。如果您不提供初始点，请设置 x0 = []。

示例

x = quadprog(problem) 返回 problem 的最小值，它是 problem 中所述的一个结构体。使用圆点表示法或 struct 函数创建 problem 结构体。或者，使用 prob2struct 从 OptimizationProblem 对象创建 problem 结构体。

示例

对于任何输入变量，[x,fval] = quadprog(___) 还会返回 fval，即在 x 处的目标函数值：

fval = 0.5*x'*H*x + f'*x

示例

[x,fval,exitflag,output] = quadprog(___) 还返回 exitflag（描述 quadprog 退出条件的整数）以及 output（包含有关优化信息的结构体）。

示例

[x,fval,exitflag,output,lambda] = quadprog(___) 还返回 lambda 结构体，其字段包含在解 x 处的拉格朗日乘数。

示例

[wsout,fval,exitflag,output,lambda] = quadprog(H,f,A,b,Aeq,beq,lb,ub,ws) 使用 ws 中的选项，从热启动对象 ws 中的数据启动 quadprog。返回的参量 wsout 包含 wsout.X 中的解点。通过在后续求解器调用中使用 wsout 作为初始热启动对象，quadprog 可以提高运行速度。

示例

全部折叠

具有线性约束的二次规划

打开实时脚本

找到下式的最小值

$f (x) = \frac{1}{2} x_{1}^{2} + x_{2}^{2} - x_{1} x_{2} - 2 x_{1} - 6 x_{2}$

需满足以下约束

$\begin{array}{l} x_{1} + x_{2} \leq 2 \\ - x_{1} + 2 x_{2} \leq 2 \\ 2 x_{1} + x_{2} \leq 3 . \end{array}$

在 quadprog 语法中，此问题可表示为最小化下式

$f (x) = \frac{1}{2} x^{T} H x + f^{T} x$ ,

其中

$\begin{array}{l} H = [\begin{matrix} 1 & - 1 \\ - 1 & 2 \end{matrix}] \\ f = [\begin{matrix} - 2 \\ - 6 \end{matrix}], \end{array}$

问题具有线性约束。

要求解此问题，首先输入系数矩阵。

H = [1 -1; -1 2]; 
f = [-2; -6];
A = [1 1; -1 2; 2 1];
b = [2; 2; 3];

调用 quadprog。

[x,fval,exitflag,output,lambda] = ...
   quadprog(H,f,A,b);

Minimum found that satisfies the constraints.

Optimization completed because the objective function is non-decreasing in 
feasible directions, to within the value of the optimality tolerance,
and constraints are satisfied to within the value of the constraint tolerance.

<stopping criteria details>

检查终点、函数值和退出标志。

x,fval,exitflag

fval = 
-8.2222

exitflag = 
1

退出标志为 1 表示结果是局部最小值。由于 H 是正定矩阵，此问题为凸型，因此最小值是全局最小值。

通过检查特征值，确认 H 是正定矩阵。

eig(H)

ans = 2×1

    0.3820
    2.6180

具有线性等式约束的二次规划

打开实时脚本

找到下式的最小值

$f (x) = \frac{1}{2} x_{1}^{2} + x_{2}^{2} - x_{1} x_{2} - 2 x_{1} - 6 x_{2}$

需满足以下约束

$x_{1} + x_{2} = 0 .$

在 quadprog 语法中，此问题可表示为最小化下式

$f (x) = \frac{1}{2} x^{T} H x + f^{T} x$ ,

其中

$\begin{array}{l} H = [\begin{matrix} 1 & - 1 \\ - 1 & 2 \end{matrix}] \\ f = [\begin{matrix} - 2 \\ - 6 \end{matrix}], \end{array}$

问题具有线性约束。

要求解此问题，首先输入系数矩阵。

H = [1 -1; -1 2]; 
f = [-2; -6];
Aeq = [1 1];
beq = 0;

调用 quadprog，为输入项 A 和 b 输入 []。

[x,fval,exitflag,output,lambda] = ...
   quadprog(H,f,[],[],Aeq,beq);

Minimum found that satisfies the constraints.

Optimization completed because the objective function is non-decreasing in 
feasible directions, to within the value of the optimality tolerance,
and constraints are satisfied to within the value of the constraint tolerance.

<stopping criteria details>

检查终点、函数值和退出标志。

x,fval,exitflag

fval = 
-1.6000

exitflag = 
1

退出标志为 1 表示结果是局部最小值。由于 H 是正定矩阵，此问题为凸型，因此最小值是全局最小值。

通过检查特征值，确认 H 是正定矩阵。

eig(H)

ans = 2×1

    0.3820
    2.6180

具有线性约束和边界的二次最小化

打开实时脚本

求使二次表达式最小的 x

$\frac{1}{2} x^{T} H x + f^{T} x$

其中

$H = [\begin{matrix} 1 & - 1 & 1 \\ - 1 & 2 & - 2 \\ 1 & - 2 & 4 \end{matrix}]$ , $f = [\begin{matrix} 2 \\ - 3 \\ 1 \end{matrix}]$ ,

需满足以下约束

$0 \leq x \leq 1$ , $\sum x = 1 / 2$ .

要求解此问题，首先输入系数。

H = [1,-1,1
    -1,2,-2
    1,-2,4];
f = [2;-3;1];
lb = zeros(3,1);
ub = ones(size(lb));
Aeq = ones(1,3);
beq = 1/2;

调用 quadprog，为输入项 A 和 b 输入 []。

x = quadprog(H,f,[],[],Aeq,beq,lb,ub)

Minimum found that satisfies the constraints.

Optimization completed because the objective function is non-decreasing in 
feasible directions, to within the value of the optimality tolerance,
and constraints are satisfied to within the value of the constraint tolerance.

<stopping criteria details>

使用非默认选项的二次最小化

打开实时脚本

设置选项以监控 quadprog 的进度。

options = optimoptions('quadprog','Display','iter');

定义具有二次目标和线性不等式约束的问题。

H = [1 -1; -1 2]; 
f = [-2; -6];
A = [1 1; -1 2; 2 1];
b = [2; 2; 3];

为了帮助编写 quadprog 函数调用，请将不必要的输入设置为 []。

Aeq = [];
beq = [];
lb = [];
ub = [];
x0 = [];

调用 quadprog 以求解问题。

x = quadprog(H,f,A,b,Aeq,beq,lb,ub,x0,options)

 Iter            Fval  Primal Infeas    Dual Infeas  Complementarity  
    0   -8.884885e+00   3.214286e+00   1.071429e-01     1.000000e+00  
    1   -8.331868e+00   1.321041e-01   4.403472e-03     1.910489e-01  
    2   -8.212804e+00   1.676295e-03   5.587652e-05     1.009601e-02  
    3   -8.222204e+00   8.381476e-07   2.793826e-08     1.809485e-05  
    4   -8.222222e+00   4.190870e-11   1.396883e-12     9.047989e-10  

Minimum found that satisfies the constraints.

Optimization completed because the objective function is non-decreasing in 
feasible directions, to within the value of the optimality tolerance,
and constraints are satisfied to within the value of the constraint tolerance.

<stopping criteria details>

基于 `prob2struct` 的二次问题

打开实时脚本

使用基于问题的优化工作流创建一个 problem 结构体。创建一个等效于具有线性约束的二次规划的优化问题。

x = optimvar('x',2);
objec = x(1)^2/2 + x(2)^2 - x(1)*x(2) - 2*x(1) - 6*x(2);
prob = optimproblem('Objective',objec);
prob.Constraints.cons1 = sum(x) <= 2;
prob.Constraints.cons2 = -x(1) + 2*x(2) <= 2;
prob.Constraints.cons3 = 2*x(1) + x(2) <= 3;

将 prob 转换为 problem 结构体。

problem = prob2struct(prob);

使用 quadprog 求解问题。

[x,fval] = quadprog(problem)

Warning: Your Hessian is not symmetric. Resetting H=(H+H')/2.

Minimum found that satisfies the constraints.

Optimization completed because the objective function is non-decreasing in 
feasible directions, to within the value of the optimality tolerance,
and constraints are satisfied to within the value of the constraint tolerance.

<stopping criteria details>

fval = 
-8.2222

返回 `quadprog` 目标函数值

打开实时脚本

求解二次规划，并返回解和目标函数值。

H = [1,-1,1
    -1,2,-2
    1,-2,4];
f = [-7;-12;-15];
A = [1,1,1];
b = 3;
[x,fval] = quadprog(H,f,A,b)

Minimum found that satisfies the constraints.

Optimization completed because the objective function is non-decreasing in 
feasible directions, to within the value of the optimality tolerance,
and constraints are satisfied to within the value of the constraint tolerance.

<stopping criteria details>

fval = 
-47.1786

检查返回的目标函数值是否与根据 quadprog 目标函数定义计算的值相匹配。

fval2 = 1/2*x'*H*x + f'*x

fval2 = 
-47.1786

检查 `quadprog` 优化过程

打开实时脚本

要查看 quadprog 的优化过程，请设置选项以显示迭代输出并返回四个输出。问题可以表示为最小化下式

$\frac{1}{2} x^{T} H x + f^{T} x$

约束条件为

$0 \leq x \leq 1$ ,

其中

$H = [\begin{matrix} 2 & 1 & - 1 \\ 1 & 3 & \frac{1}{2} \\ - 1 & \frac{1}{2} & 5 \end{matrix}]$ , $f = [\begin{matrix} 4 \\ - 7 \\ 12 \end{matrix}]$ .

输入问题系数。

H = [2 1 -1
    1 3 1/2
    -1 1/2 5];
f = [4;-7;12];
lb = zeros(3,1);
ub = ones(3,1);

设置选项以显示求解器的迭代进度。

options = optimoptions('quadprog','Display','iter');

调用带有四个输出的 quadprog。

[x fval,exitflag,output] = quadprog(H,f,[],[],[],[],lb,ub,[],options)

 Iter            Fval  Primal Infeas    Dual Infeas  Complementarity  
    0    2.691769e+01   1.582123e+00   1.712849e+01     1.680447e+00  
    1   -3.889430e+00   0.000000e+00   8.564246e-03     9.971731e-01  
    2   -5.451769e+00   0.000000e+00   4.282123e-06     2.710131e-02  
    3   -5.499995e+00   0.000000e+00   2.878422e-10     1.750743e-06  
    4   -5.500000e+00   0.000000e+00   1.454808e-13     8.753723e-10  

Minimum found that satisfies the constraints.

Optimization completed because the objective function is non-decreasing in 
feasible directions, to within the value of the optimality tolerance,
and constraints are satisfied to within the value of the constraint tolerance.

<stopping criteria details>

fval = 
-5.5000

exitflag = 
1

output = struct with fields:
            message: 'Minimum found that satisfies the constraints.↵↵Optimization completed because the objective function is non-decreasing in ↵feasible directions, to within the value of the optimality tolerance,↵and constraints are satisfied to within the value of the constraint tolerance.↵↵<stopping criteria details>↵↵Optimization completed: The relative dual feasibility, 1.212340e-14,↵is less than options.OptimalityTolerance = 1.000000e-08, the complementarity measure,↵8.753723e-10, is less than options.OptimalityTolerance, and the relative maximum constraint↵violation, 0.000000e+00, is less than options.ConstraintTolerance = 1.000000e-08.'
          algorithm: 'interior-point-convex'
      firstorderopt: 2.3577e-09
    constrviolation: 0
         iterations: 4
       linearsolver: 'dense'
       cgiterations: []

返回 `quadprog` 拉格朗日乘数

打开实时脚本

求解二次规划问题并返回拉格朗日乘数。

H = [1,-1,1
    -1,2,-2
    1,-2,4];
f = [-7;-12;-15];
A = [1,1,1];
b = 3;
lb = zeros(3,1);
[x,fval,exitflag,output,lambda] = quadprog(H,f,A,b,[],[],lb);

Minimum found that satisfies the constraints.

Optimization completed because the objective function is non-decreasing in 
feasible directions, to within the value of the optimality tolerance,
and constraints are satisfied to within the value of the constraint tolerance.

<stopping criteria details>

检查拉格朗日乘数结构体 lambda。

disp(lambda)

    ineqlin: 12.0000
      eqlin: [0×1 double]
      lower: [3×1 double]
      upper: [3×1 double]

线性不等式约束有一个相关联的拉格朗日乘数 12。

显示与下界相关联的乘数。

disp(lambda.lower)

    5.0000
    0.0000
    0.0000

只有 lambda.lower 的第一个分量具有非零乘数。这通常意味着只有 x 的第一个分量位于下界（即零）上。这可通过显示 x 的分量进行确认。

disp(x)

    0.0000
    1.5000
    1.5000

返回热启动对象

打开实时脚本

要加速后续的 quadprog 调用，请创建一个热启动对象。

options = optimoptions('quadprog','Algorithm','active-set');
x0 = [1 2 3];
ws = optimwarmstart(x0,options);

使用 ws 求解二次规划。

H = [1,-1,1
    -1,2,-2
    1,-2,4];
f = [-7;-12;-15];
A = [1,1,1];
b = 3;
lb = zeros(3,1);
tic
[ws,fval,exitflag,output,lambda] = quadprog(H,f,A,b,[],[],lb,[],ws);

Minimum found that satisfies the constraints.

Optimization completed because the objective function is non-decreasing in 
feasible directions, to within the value of the optimality tolerance,
and constraints are satisfied to within the value of the constraint tolerance.

<stopping criteria details>

toc

Elapsed time is 0.060411 seconds.

更改目标函数，重新求解问题。

f = [-10;-15;-20];

tic
[ws,fval,exitflag,output,lambda] = quadprog(H,f,A,b,[],[],lb,[],ws);

Minimum found that satisfies the constraints.

Optimization completed because the objective function is non-decreasing in 
feasible directions, to within the value of the optimality tolerance,
and constraints are satisfied to within the value of the constraint tolerance.

<stopping criteria details>

toc

Elapsed time is 0.010756 seconds.

输入参数

全部折叠

`H` — 二次目标项
对称实矩阵

二次目标项，指定为对称实矩阵。H 以 1/2*x'*H*x + f'*x 表达式形式表示二次矩阵。如果 H 不对称，quadprog 会发出警告，并改用对称版本 (H + H')/2。

如果二次矩阵 H 为稀疏矩阵，则默认情况下，'interior-point-convex' 算法使用的算法与 H 为稠密矩阵时略有不同。通常，对于大型稀疏问题，稀疏算法更快，对于稠密或小型问题，稠密算法更快。有关详细信息，请参阅 LinearSolver 选项说明和interior-point-convex quadprog 算法。

示例: [2,1;1,3]

数据类型: single | double

`f` — 线性目标项
实数向量

线性目标项，指定为实数向量。f 表示 1/2*x'*H*x + f'*x 表达式中的线性项。

示例: [1;3;2]

数据类型: single | double

`A` — 线性不等式约束
实矩阵

线性不等式约束，指定为实矩阵。A 是 M×N 矩阵，其中 M 是不等式的数目，而 N 是变量的数目（x0 中的元素数）。对于大型问题，如果使用支持稀疏数据的算法，则可将 A 作为稀疏矩阵传递。请参阅稀疏性在优化算法中的应用。

A 以如下形式编写 M 个线性不等式

A*x <= b,

其中，x 是由 N 个变量组成的列向量 x(:)，b 是具有 M 个元素的列向量。

例如，假设有以下不等式：

x₁ +2x₂ ≤10
3x₁ +4x₂ ≤20
5x₁ +6x₂ ≤30，

通过输入以下约束来指定不等式。

A = [1,2;3,4;5,6];
b = [10;20;30];

示例: 要指定 x 分量总和等于或小于 1，请使用 A = ones(1,N) 和 b = 1。

数据类型: single | double

`b` — 线性不等式约束
实数向量

线性不等式约束，指定为实数向量。b 是与 A 矩阵相关的包含 M 个元素的向量。如果将 b 作为行向量传递，求解器会在内部将 b 转换为列向量 b(:)。

b 以如下形式编写 M 个线性不等式

A*x <= b,

其中，x 是由 N 个变量组成的列向量 x(:)，A 是大小为 M×N 的矩阵。

例如，假设有以下不等式：

x₁ + 2x₂ ≤ 10
3x₁ + 4x₂ ≤ 20
5x₁ + 6x₂ ≤ 30。

通过输入以下约束来指定不等式。

A = [1,2;3,4;5,6];
b = [10;20;30];

示例: 要指定 x 分量总和等于或小于 1，请使用 A = ones(1,N) 和 b = 1。

数据类型: single | double

`Aeq` — 线性等式约束
实矩阵

线性等式约束，指定为实矩阵。Aeq 是 Me×N 矩阵，其中 Me 是等式的数目，而 N 是变量的数目（x0 中的元素数）。对于大型问题，如果算法支持稀疏数据，则可将 A 作为稀疏矩阵传递。请参阅稀疏性在优化算法中的应用。

Aeq 以如下形式编写 Me 个线性等式

Aeq*x = beq,

其中，x 是由 N 个变量组成的列向量 x(:)，beq 是具有 Me 个元素的列向量。

例如，假设有以下不等式：

x₁ +2x₂ +3x₃ =10
2x₁ +4x₂ + x₃ =20，

通过输入以下约束来指定不等式。

Aeq = [1,2,3;2,4,1];
beq = [10;20];

示例: 要指定 x 分量总和为 1，请使用 Aeq = ones(1,N) 和 beq = 1。

数据类型: single | double

`beq` — 线性等式约束
实数向量

线性等式约束，指定为实数向量。beq 是与 Aeq 矩阵相关的包含 Me 个元素的向量。如果将 beq 作为行向量传递，求解器会在内部将 beq 转换为列向量 beq(:)。

beq 以如下形式编写 Me 个线性等式

Aeq*x = beq,

其中，x 是由 N 个变量组成的列向量 x(:)，Aeq 是大小为 Me×N 的矩阵。

例如，请参考以下等式：

x₁ + 2x₂ + 3x₃ = 10
2x₁ + 4x₂ + x₃ = 20。

通过输入以下约束来指定等式。

Aeq = [1,2,3;2,4,1];
beq = [10;20];

示例: 要指定 x 分量总和为 1，请使用 Aeq = ones(1,N) 和 beq = 1。

数据类型: single | double

`lb` — 下界
实数向量 | 实数数组

下界，指定为实数向量或实数数组。如果 x0 中的元素数等于 lb 中的元素数，则 lb 指定

x(i) >= lb(i)（对于全部 i）。

如果 numel(lb) < numel(x0)，则 lb 指定

x(i) >= lb(i) (1 <= i <= numel(lb))。

如果 lb 的元素数少于 x0，求解器将发出警告。

示例: 要指定所有 x 分量为正，请使用 lb = zeros(size(x0))。

数据类型: single | double

`ub` — 上界
实数向量 | 实数数组

上界，指定为实数向量或实数数组。如果 x0 中的元素数等于 ub 中的元素数，则 ub 指定

x(i) <= ub(i)（对于全部 i）。

如果 numel(ub) < numel(x0)，则 ub 指定

x(i) <= ub(i) (1 <= i <= numel(ub))。

如果 ub 的元素数少于 x0，求解器将发出警告。

示例: 要指定 x 的所有分量小于 1，请使用 ub = ones(size(x0))。

数据类型: single | double

`x0` — 初始点
实数向量

初始点，指定为实数向量。x0 的长度是 H 的行数或列数。

当问题只有边界约束时，x0 适用于 'trust-region-reflective' 算法。x0 也适用于 'active-set' 算法。

注意

x0 是 'active-set' 算法的必需参量。

如果您未指定 x0，quadprog 会将 x0 的所有分量设置为由边界定义的框内部的一个点。对于 'interior-point-convex' 算法和具有等式约束的 'trust-region-reflective' 算法，quadprog 将忽略 x0。

示例: [1;2;1]

数据类型: single | double

`options` — 优化选项
`optimoptions` 的输出 | 结构体，例如 `optimset` 返回的结构体

优化选项，指定为 optimoptions 的输出或 optimset 等返回的结构体。

optimoptions 显示中缺少某些选项。这些选项在下表中以斜体显示。有关详细信息，请参阅查看优化选项。

所有算法

`Algorithm`	选择算法： `'interior-point-convex'`（默认值） `'trust-region-reflective'` `'active-set'` `'interior-point-convex'` 算法只处理凸问题。`'trust-region-reflective'` 算法处理只有边界或只有线性等式约束的问题，但不处理同时具有两者的问题。`'active-set'` 算法处理不定问题，前提是 `H` 在 `Aeq` 的零空间上的投影是半正定的。有关详细信息，请参阅选择算法。
Diagnostics	显示关于要最小化或求解的函数的诊断信息。选项是 `'on'` 或 `'off'`（默认值）。
`Display`	显示级别（请参阅迭代输出）： `'off'` 或 `'none'` 不显示输出。 `'final'` 仅显示最终输出（默认值）。 `'interior-point-convex'` 和 `'active-set'` 算法允许附加值： `'iter'` 指定迭代输出。 `'iter-detailed'` 指定迭代输出以及详细的退出消息。 `'final-detailed'` 仅显示最终输出以及详细的退出消息。
`MaxIterations`	允许的最大迭代次数；为非负整数。对于 `'trust-region-reflective'` 等式约束问题，默认值为 `2(numberOfVariables – numberOfEqualities)`。 `'active-set'` 的默认值为 `10(numberOfVariables + numberOfConstraints)`。对于所有其他算法和问题，默认值为 `200`。对于 `optimset`，选项名称为 `MaxIter`。请参阅当前选项名称和旧选项名称。
`OptimalityTolerance`	一阶最优性的终止容差；非负标量。对于 `'trust-region-reflective'` 等式约束问题，默认值为 `1e-6`。对于 `'trust-region-reflective'` 边界约束问题，默认值为 `100*eps`，大约为 `2.2204e-14`。对于 `'interior-point-convex'` 和 `'active-set'` 算法，默认值为 `1e-8`。请参阅容差和停止条件。对于 `optimset`，选项名称为 `TolFun`。请参阅当前选项名称和旧选项名称。
`StepTolerance`	`x` 的终止容差；非负标量。对于 `'trust-region-reflective'`，默认值为 `100*eps`，大约为 `2.2204e-14`。对于 `'interior-point-convex'`，默认值为 `1e-12`。对于 `'active-set'`，默认值为 `1e-8`。对于 `optimset`，选项名称为 `TolX`。请参阅当前选项名称和旧选项名称。

仅 'trust-region-reflective' 算法

`FunctionTolerance`	函数值的终止容差；非负标量。默认值取决于问题类型：边界约束问题使用 `100*eps`，线性等式约束问题使用 `1e-6`。请参阅容差和停止条件。对于 `optimset`，选项名称为 `TolFun`。请参阅当前选项名称和旧选项名称。
`HessianMultiplyFcn`	黑塞矩阵乘法函数，指定为函数句柄。对于大规模结构问题，此函数计算黑塞矩阵乘积 `HY`，而并不实际构造 `H`。函数具有以下形式 W = hmfun(Hinfo,Y) 其中 `Hinfo`（可能还有一些附加参数）包含用于计算 `HY` 的矩阵。有关使用此选项的示例，请参阅使用密集、结构化的 Hessian 矩阵进行二次最小化。对于 `optimset`，选项名称为 `HessMult`。请参阅当前选项名称和旧选项名称。
MaxPCGIter	PCG（预条件共轭梯度）迭代的最大次数；正标量。对于边界约束问题，默认值为 `max(1,floor(numberOfVariables/2))`。对于等式约束问题，`quadprog` 将忽略 `MaxPCGIter` 并使用 `MaxIterations` 来限制 PCG 迭代的次数。有关详细信息，请参阅预条件共轭梯度法。
PrecondBandWidth	PCG 的预条件子的上带宽；非负整数。默认情况下，`quadprog` 使用对角预条件（上带宽 `0`）。对于某些问题，增加带宽会减少 PCG 迭代次数。将 `PrecondBandWidth` 设置为 `Inf` 会使用直接分解（乔列斯基分解），而不是共轭梯度 (CG)。直接分解的计算成本较 CG 高，但所得的求解步质量更好。
`SubproblemAlgorithm`	确定迭代步的计算方式。与 `'factorization'` 相比，默认值 `'cg'` 采用的步执行速度更快，但不够准确。请参阅trust-region-reflective quadprog 算法。
TolPCG	PCG 迭代的终止容差：正标量。默认值为 `0.1`。
`TypicalX`	典型的 `x` 值。`TypicalX` 中的元素数等于起点 `x0` 中的元素数。默认值为 `ones(numberOfVariables,1)`。`quadprog` 在内部使用 `TypicalX` 进行缩放。仅当 `x` 具有无界分量且一个无界分量的 `TypicalX` 值超过 `1` 时，`TypicalX` 才会起作用。

仅 'interior-point-convex' 算法

ConstraintTolerance

约束违反值的容差；为非负标量。默认值为 1e-8。

对于 optimset，选项名称为 TolCon。请参阅当前选项名称和旧选项名称。

LinearSolver

算法内部线性求解器的类型：

'auto'（默认值）- 如果 H 矩阵为稀疏矩阵，则使用 'sparse'，否则使用 'dense'。
'sparse' - 使用稀疏线性代数。请参阅稀疏矩阵。
'dense' - 使用稠密线性代数。

ScaleProblem

当 true 时，执行内部缩放以改善问题条件，并可能获得更快或更准确的解。默认值为 false。

对于一些线性约束（A 或 Aeq）或二次目标系数（H）矩阵缩放不佳的问题，true 设置可以显著提高速度或提高解的精度。但是，ScaleProblem=true 会给求解器增加一点时间开销，在某些情况下还会导致收敛性差。

仅 'active-set' 算法

ConstraintTolerance

约束违反值的容差；为非负标量。默认值为 1e-8。

对于 optimset，选项名称为 TolCon。请参阅当前选项名称和旧选项名称。

ObjectiveLimit

容差（停止条件），标量。如果目标函数值低于 ObjectiveLimit 并且当前点可行，则迭代停止，因为问题很可能是无界的。默认值为 -1e20。

UseCodegenSolver

对使用目标硬件上运行的软件版本的指示，指定为 true 或默认 false。使用此选项可在生成代码前在桌面环境中测试代码。您可以在生成代码时传递此选项，但它对代码生成没有影响。

单精度代码生成

`Algorithm`	必须是 `'active-set'`。
`ConstraintTolerance`	约束违反值容差；正标量。默认值为 `1e-4`。对于 `optimset`，选项名称为 `TolCon`。请参阅当前选项名称和旧选项名称。
`MaxIterations`	允许的最大迭代次数，非负整数。默认值为 `10*(nVar + mConstr)`，其中 `nVar` 是问题变量的数量，`mConstr` 是约束的数量。
`ObjectiveLimit`	容差（停止条件），标量。如果目标函数值低于 `ObjectiveLimit` 并且当前点可行，则迭代停止，因为问题很可能是无界的。默认值为 `-1e20`。
`OptimalityTolerance`	一阶最优性的终止容差，正标量。默认值为 `1e-4`。请参阅一阶最优性测度。对于 `optimset`，名称是 `TolFun`。请参阅当前选项名称和旧选项名称。
`StepTolerance`	关于正标量 `x` 的终止容差。默认值为 `1e-4`。对于 `optimset`，选项名称为 `TolX`。请参阅当前选项名称和旧选项名称。
`UseCodegenSolver`	对使用目标硬件上运行的软件版本的指示，指定为 `true` 或默认 `false`。使用此选项可在生成代码前在桌面环境中测试代码。您可以在生成代码时传递此选项，但它对代码生成没有影响。

`problem` — 问题结构体
结构体

问题结构体，指定为具有以下字段的结构体：

`H`	`1/2x'H*x` 中的对称矩阵
`f`	线性项 `f'*x` 中的向量
`Aineq`	线性不等式约束 `Aineq*x` ≤ `bineq` 中的矩阵
`bineq`	线性不等式约束 `Aineq*x` ≤ `bineq` 中的向量
`Aeq`	线性等式约束 `Aeq*x = beq` 中的矩阵
`beq`	线性等式约束 `Aeq*x = beq` 中的向量
`lb`	由下界组成的向量
`ub`	由上界组成的向量
`x0`	`x` 的初始点
`solver`	`'quadprog'`
`options`	使用 `optimoptions` 或 `optimset` 创建的选项

必需字段有 H、f、solver 和 options。在求解时，quadprog 忽略 problem 中上面列出的字段以外的任何字段。

注意

您不能将热启动与 problem 参量结合使用。

数据类型: struct

`ws` — 热启动对象
使用 `optimwarmstart` 创建的对象

热启动对象，指定为使用 optimwarmstart 创建的对象。热启动对象包含起点和选项，以及代码生成中的内存大小数据（可选）。请参阅热启动最佳实践。

示例: ws = optimwarmstart(x0,options)

输出参量

全部折叠

`x` — 解
实数向量

解，以实数向量形式返回。x 是在满足所有边界和线性约束的条件下对 1/2*x'*H*x + f'*x 进行最小化的向量。x 可以是非凸问题的局部最小值。对于凸问题，x 是全局最小值。有关详细信息，请参阅局部最优与全局最优。

`wsout` — 热启动对象求解
`QuadprogWarmStart` 对象

热启动对象求解，以 QuadprogWarmStart 对象形式返回。解点是 wsout.X。

您可以在后续的 quadprog 调用中使用 wsout 作为输入热启动对象。

`fval` — 解处的目标函数值
实数标量

在解处的目标函数值，以实数标量形式返回。fval 是 1/2*x'*H*x + f'*x 在解 x 处的值。

`exitflag` — `quadprog` 停止的原因
整数

quadprog 停止的原因，以下表中所述的整数形式返回。

所有算法
`1`	函数收敛于解 `x`。
`0`	迭代次数超出 `options.MaxIterations`。
`-2`	问题不可行。或者，对于 `'interior-point-convex'`，步长小于 `options.StepTolerance`，但不满足约束。
`-3`	问题无界。
`'interior-point-convex'` 算法
`2`	步长小于 `options.StepTolerance`，也满足约束。
`-6`	检测到非凸问题。
`-8`	无法计算步的方向。
`'trust-region-reflective'` 算法
`4`	找到局部最小值；最小值不唯一。
`3`	目标函数值的变化小于 `options.FunctionTolerance`。
`-4`	当前搜索方向不是下降方向。无法取得进一步进展。
`'active-set'` 算法
`-6`	检测到非凸问题；`H` 在 `Aeq` 的零空间上的投影不是半正定的。

注意

有时，在问题实际无界时，'active-set' 算法会停止并返回退出标志 0。设置更高的迭代限制也会返回退出标志 0。

`output` — 有关优化过程的信息
结构体

有关优化过程的信息，以包含下列字段的结构体形式返回：

`iterations`	执行的迭代次数
`algorithm`	使用的优化算法
`cgiterations`	PCG 迭代总数（仅适用于 `'trust-region-reflective'` 算法）
`constrviolation`	约束函数的最大值
`firstorderopt`	一阶最优性的测度
`linearsolver`	内部线性求解器的类型，`'dense'` 或 `'sparse'`（仅适用于 `'interior-point-convex'` 算法）
`message`	退出消息

`lambda` — 解处的拉格朗日乘数
结构体

在解处的拉格朗日乘数，以包含下列字段的结构体形式返回：

`lower`	下界 `lb`
`upper`	上界 `ub`
`ineqlin`	线性不等式
`eqlin`	线性等式

有关详细信息，请参阅拉格朗日乘数结构体。

详细信息

全部折叠

增强版退出消息

接下来的几项列出了可能增强的退出消息 quadprog。增强的退出消息在消息的第一句中给出了更多信息的链接。

找到满足约束的最小值

求解器找到一个满足所有边界约束和线性约束的最小化点。由于问题是凸问题，该最小化点是全局最小值。有关详细信息，请参阅局部最优与全局最优。

求解器停滞，约束满足

求解器停止，因为最后一步太小了。当相对步长低于 StepTolerance 容差，则迭代结束。有时，这意味着求解器找到了最小值。然而，一阶最优性度量不低于 OptimalityTolerance，因此结果可能不准确。所有约束均已满足。

要继续，请尝试以下操作：

检查 output 结构中的一阶最优性度量。如果一阶最优性度量很小，那么返回的解很可能是准确的。
将 StepTolerance 选项设置为 0。有时，此设置可帮助求解器继续进行，但有时求解器会因其他问题而停滞。
尝试不同算法。如果求解器提供了多得算法选择，有时尝试不同的算法可能会成功。
尝试删除依赖约束。这可以确保没有任何多余的线性约束。

问题似乎是无界问题

quadprog 停止，因为它似乎找到了一个满足所有约束并导致目标函数无限下降的方向

要继续，请：

确保每个分量都有有限的边界。
检查目标函数以确保它是严格凸函数（即二次矩阵的特征值严格为正）。
查看相关的线性规划问题（即没有二次项的原始问题）是否有有限解。

无法计算步进方向

求解器无法继续，因为它无法计算出一个通向最小值的方向。这很可能是由于冗余的线性约束或容差过小所导致的。

要继续，请：

检查线性约束矩阵是否存在冗余。尝试识别并消除冗余的线性约束。
确保您的 FunctionTolerance、OptimalityTolerance 和 ConstraintTolerance 选项大于 1e-14，最好大于 1e-12。请参阅容差和停止条件。

此问题是非凸问题

quadprog 确定问题不是凸。尝试不同算法。有关详细信息，请参阅二次规划算法。

预求解期间找到解

求解器在预求解阶段找到了解。这意味着有了此边界、线性约束和 f（线性目标系数）可以立即找到解。有关详细信息，请参阅预求解/后求解。

此问题不可行

在预求解过程中，求解器发现问题的表达式不一致。不一致意味着并非所有约束都能在一个点 x 上得到满足。有关详细信息，请参阅预求解/后求解。

此问题无界

在预求解过程中，求解器找到一个可行方向，在该方向上目标函数无边界地递减。有关详细信息，请参阅预求解/后求解。

收敛于不可行点

quadprog 收敛到不满足所有约束的点，在约束范围内容差称为ConstraintTolerance。quadprog 停止的原因是上一个步长太小。当相对步长低于 StepTolerance 容忍度，则迭代结束。

有关如何继续的建议，请参阅quadprog 收敛于不可行点。

找不到可行的解

求解器收敛到不满足所有约束的点，在约束范围内容差称为ConstraintTolerance。求解器停止的原因是上一个步长太小。当相对步长低于 StepTolerance 容忍度，则迭代结束。

找不到可行的解

不存在满足所有边界和线性约束的点。有关检查不一致的线性约束的帮助，请参阅调查线性不可行性。

找到最佳解

只有一个可行点。独立线性等式约束的数量与问题中的变量数量相同。

找到最佳解

求解器停止，因为一阶最优性度量小于 OptimalityTolerance 容差。

一阶最优性度量是投影梯度的无穷范数。投影是投影到线性等式矩阵 Aeq 的零空间上。

找到局部最小值

求解器停止在零曲率点处，即局部最小值处。存在其他具有相同目标函数值的可行点。

此问题无界

存在零曲率或负曲率方向，目标函数沿着这些方向无限减小。因此，对于任何目标值，都存在目标值小于目标的可行点。检查问题中是否包含足够的约束，例如所有变量的边界。

找到最佳解

求解器停止，因为一阶最优性度量小于 OptimalityTolerance 容差。

可能是局部最小值

求解器停止，因为函数值的相对变化低于 FunctionTolerance容差。要检查解的质量，请参阅可能是局部最小值。

可能是局部最小值

求解器停止，因为函数值的相对变化低于 FunctionTolerance 的平方根容差，且前几次迭代中函数值的变化量减小的幅度小于 3.5 倍。当目标函数值的差异相对较小，但不能足够快地减小到零时，此条件会停止求解器。要检查解的质量，请参阅可能是局部最小值。

退出消息的定义

接下来的几项包含以下术语的定义 quadprog 退出消息。

容差

一般来说，容差是一个阈值，超过阈值时将终止求解器的迭代。有关容差的详细信息，请参阅容差和停止条件。

凸

如果从任何可行点都不存在具有负曲率的可行方向，则二次规划问题为凸问题。凸问题只有一个局部最小值，它也是全局最小值。

可行方向

来自可行点 x 的可行方向是满足以下条件的向量 v：对于足够小的正 a，x + av 可行。

可行点是一个满足所有约束的点。

`StepTolerance`

StepTolerance 是一个容差最后一步的大小，即评估 fsolve 位置变化的大小。

`OptimalityTolerance`

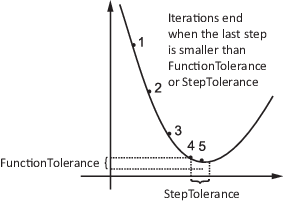
称为 OptimalityTolerance 的容差与一阶最优性测度相关。当一阶最优性测度小于 OptimalityTolerance 时，迭代结束。

对于约束问题，一阶最优性测度是以下两个量的最大值：

$\begin{array}{l} ‖ \nabla_{x} L (x, λ ‖ = ‖ \nabla f (x) + A^{T} λ_{i n e q l i n} + A e q^{T} λ_{e q l i n} \\ + \sum λ_{i n e q n o n l i n, i} \nabla c_{i} (x) + \sum λ_{e q n o n l i n, i} \nabla c e q_{i} (x) ‖, \end{array}$

$‖ \vec{| l_{i} - x_{i} | λ_{l o w e r, i}}, \vec{| x_{i} - u_{i} | λ_{u p p e r, i}}, \vec{| {(A x - b)}_{i} | λ_{i n e q l i n, i}}, \vec{| c_{i} (x) | λ_{i n e q n o n l i n, i}} ‖ .$

对于无约束问题，一阶最优性测度是梯度向量分量绝对值的最大值（也称为无穷范数）。

一阶最优性测度在最小化点上应为零。

有关详细信息，包括这些方程中所有变量的定义，请参阅一阶最优性测度。

有界问题的一阶最优性测度

对于无约束问题，一阶最优性测度是梯度向量分量绝对值的最大值（也称为梯度的无穷范数）。在最小化点处，此值应为零。

对于有边界问题，一阶最优性测度是最大值除以 |v_i*g_i| 的 i。此处，g_i 是梯度的第 i 个分量，x 是当前点，并且

$v_{i} = {\begin{array}{l} | x_{i} - b_{i} | & if the negative gradient points toward bound b_{i} \\ 1 & otherwise . \end{array}$

如果 x_i 位于边界上，则 v_i 为零。如果 x_i 不在边界上，则在最小化点上，梯度 g_i 应为零。因此，一阶最优性测度在最小化点上应为零。

有关详细信息，请参阅一阶最优性测度。

`ConstraintTolerance`

约束容差称为 ConstraintTolerance，是当前点所有约束函数值的最大值。

ConstraintTolerance 的运算原理不同于其他容差。如果不满足 ConstraintTolerance（即，如果约束函数的模超过 ConstraintTolerance），求解器将尝试继续求解，除非因其他原因而停止。求解器不会仅仅因为满足 ConstraintTolerance 就停止。

相对对偶可行性

对偶可行性 r_d 是根据问题的 KKT 条件定义的。相对对偶可行性停止条件为

r_d ≤ ρOptimalityTolerance， (1)

其中 ρ 是缩放因子。

有关详细信息，请参阅预测-校正。

双重可行性

KKT 条件状态，在最优 x 下，存在拉格朗日乘数 ${\bar{λ}}_{ineq}$ 和 λ_eq，使得

$\begin{matrix} H x + c + A_{eq}^{T} λ_{eq} + {\bar{A}}^{T} {\bar{λ}}_{ineq} = 0 \\ \bar{A} x - \bar{b} + s = 0 \\ A_{eq} x - b_{eq} = 0 \\ s_{i} {\bar{λ}}_{ineq, i} = 0 \\ s_{i} \geq 0 \\ {\bar{λ}}_{ineq, i} \geq 0. \end{matrix}$

变量 $\bar{A}$ 、 ${\bar{λ}}_{ineq}$ 和 $\bar{b}$ 包含边界作为线性不等式的一部分。

对偶可行性 r_d 是 $r_{d} = H x + c + A_{eq}^{T} λ_{eq} + {\bar{A}}^{T} {\bar{λ}}_{ineq}$ 的绝对值。

缩放因子

缩放因子 ρ 为

$ρ = \max (1, ‖ H ‖, ‖ \bar{A} ‖, ‖ A_{e q} ‖, ‖ c ‖, ‖ \bar{b} ‖, ‖ b_{e q} ‖) .$

范数 $‖ \cdot ‖$ 是表达式中元素的最大绝对值。

互补性测度

互补性测度是根据问题的 KKT 条件定义的。在最优 x 下，拉格朗日乘数 ${\bar{λ}}_{ineq}$ 和 λ_eq 使得

变量 $\bar{A}$ 、 ${\bar{λ}}_{ineq}$ 和 $\bar{b}$ 包含边界作为线性不等式的一部分。

互补性测度为：

$\sum_{i} s_{i} {\bar{λ}}_{ineq, i} .$

有关详细信息，请参阅预测-校正。

总相对误差

总相对误差是根据问题的 KKT 条件定义的。总相对误差停止条件成立时评价函数φ 满足

φ ≥ max(OptimalityTolerance,10⁵φ_min)。 (2)

当该停止条件成立时，求解器确定二次规划不可行。

评价函数

KKT 条件状态，在最优 x 下，存在拉格朗日乘数 ${\bar{λ}}_{ineq}$ 和 λ_eq，使得

变量 $\bar{A}$ 、 ${\bar{λ}}_{ineq}$ 和 $\bar{b}$ 包含边界作为线性不等式的一部分。

φ 评价函数是

$\frac{1}{ρ} (\max ({‖ r_{eq} ‖}_{\infty}, {‖ r_{ineq} ‖}_{\infty}, {‖ r_{d} ‖}_{\infty}) + g) .$

φ 定义中的术语：

$\begin{matrix} ρ = \max (1, ‖ H ‖, ‖ \bar{A} ‖, ‖ A_{e q} ‖, ‖ c ‖, ‖ \bar{b} ‖, ‖ b_{e q} ‖) \\ r_{eq} = A_{eq} x - b_{eq} \\ r_{ineq} = \bar{A} x - \bar{b} + s \\ r_{d} = H x + c + A_{eq}^{T} λ_{eq} + {\bar{A}}^{T} {\bar{λ}}_{ineq} \\ g = x^{T} H x + f^{T} x - \bar{b} {\bar{λ}}_{ineq} - b_{eq} λ_{eq} . \end{matrix}$

表达式 φ_min 表示在所有迭代中看到的 φ 的最小值。

预求解

预求解是一组用于简化线性或二次规划问题的算法。这些算法寻找简单的不一致问题，例如不一致的边界和线性约束。它们也寻找冗余的边界和线性不等式。有关详细信息，请参阅预求解/后求解。

问题似乎病态

内部计算的搜索方向未能降低目标函数值。可能是因为问题的缩放不佳或存在病态矩阵（quadprog 中的 H，lsqlin 中的 C）。有关如何继续的建议，请参阅当求解器失败时或可能是局部最小值。

算法

全部折叠

`'interior-point-convex'`

'interior-point-convex' 算法尝试遵循严格在约束范围内的路径。它使用预求解模块来消除冗余，并通过求解简单的分量来简化问题。

该算法针对稀疏黑塞矩阵 H 和稠密矩阵有不同的实现。通常，对于大型稀疏问题，稀疏实现更快，对于稠密或小型问题，稠密实现更快。有关详细信息，请参阅interior-point-convex quadprog 算法。

`'trust-region-reflective'`

'trust-region-reflective' 算法基于 [1] 中所述的内部反射牛顿法的子空间信赖域方法。每次迭代都涉及使用预条件共轭梯度法 (PCG) 来近似求解大型线性系统。有关详细信息，请参阅trust-region-reflective quadprog 算法。

`'active-set'`

'active-set' 算法是一种投影方法，类似于 [2] 中所述的方法。该算法不使用稀疏数据；请参阅稀疏性在优化算法中的应用。有关详细信息，请参阅active-set quadprog 算法。

热启动

热启动对象维护先前已求解问题的活动约束列表。求解器将尽可能多地携带活动约束信息来求解当前问题。如果前一个问题与当前问题差异太大，则不会重用任何活动约束集信息。在这种情况下，求解器实际上执行冷启动，以重新构建活动约束列表。

替代功能

App

优化实时编辑器任务为 quadprog 提供了一个可视化界面。

参考

[1] Coleman, T. F., and Y. Li. “A Reflective Newton Method for Minimizing a Quadratic Function Subject to Bounds on Some of the Variables.” SIAM Journal on Optimization. Vol. 6, Number 4, 1996, pp. 1040–1058.

[2] Gill, P. E., W. Murray, and M. H. Wright. Practical Optimization. London: Academic Press, 1981.

[3] Gould, N., and P. L. Toint. “Preprocessing for quadratic programming.” Mathematical Programming. Series B, Vol. 100, 2004, pp. 95–132.

扩展功能

全部展开

C/C++ 代码生成
使用 MATLAB® Coder™ 生成 C 代码和 C++ 代码。

用法说明和限制：

quadprog 支持使用 codegen (MATLAB Coder) 函数或 MATLAB^® Coder™ 生成代码。您必须拥有 MATLAB Coder 许可证才能生成代码。
目标硬件必须支持标准双精度浮点计算或标准单精度浮点计算。
代码生成目标与 MATLAB 求解器不使用相同的数学核心函数库。因此，代码生成解可能不同于求解器解，尤其是对于病态问题。
要在生成代码前在 MATLAB 中测试代码，请将 UseCodegenSolver 选项设置为 true。这样，求解器便可使用代码生成创建的相同代码。
在生成代码时，quadprog 不支持 problem 参量。
```
[x,fval] = quadprog(problem) % Not supported
```
所有 quadprog 输入矩阵（如 A、Aeq、lb 和 ub）都必须是满矩阵，而不能是稀疏矩阵。您可以使用 full 函数将稀疏矩阵转换为满矩阵。
lb 和 ub 参量的条目数必须与 H 中的列数相同，或必须为空 []。
如果您的目标硬件不支持无限边界，请使用 optim.coder.infbound。
对于涉及嵌入式处理器的高级代码优化，您还需要 Embedded Coder^® 许可证。
您必须包括适用于 quadprog 的选项，并使用 optimoptions 指定这些选项。选项中必须包括 Algorithm 并将其设置为 'active-set'。
```
options = optimoptions("quadprog",Algorithm="active-set");
[x,fval,exitflag] = quadprog(H,f,A,b,Aeq,beq,lb,ub,x0,options);
```
代码生成支持以下选项：
- Algorithm - 必须为 'active-set'
- ConstraintTolerance
- MaxIterations
- ObjectiveLimit
- OptimalityTolerance
- StepTolerance
- UseCodegenSolver

生成的代码只会对选项进行有限的错误检查。更新选项的推荐方法是使用 optimoptions，而不是圆点表示法。

opts = optimoptions('quadprog','Algorithm','active-set');
opts = optimoptions(opts,'MaxIterations',1e4); % Recommended
opts.MaxIterations = 1e4; % Not recommended

不要从文件中加载选项。否则会导致代码生成失败。请在代码中创建选项。
如果您指定了不受支持的选项，在代码生成过程中通常会忽略该选项。为了获得可靠的结果，请仅指定支持的选项。

有关示例，请参阅为 quadprog 生成代码。

版本历史记录

在 R2006a 之前推出

全部展开

R2025a: 生成代码前测试

将新的 UseCodegenSolver 选项设置为 true，以便 quadprog 使用与代码生成所创建软件相同的版本。通过此选项，可以在生成代码或将代码部署到硬件之前检查求解器的行为。对于支持单精度代码生成的求解器，生成的代码也可以支持单精度硬件。您可以在生成代码时包含该选项；该选项对代码生成没有影响，但保留该选项可以省去删除它的步骤。尽管生成的代码与 MATLAB 代码相同，但结果可能因链接的数学库不同而略有差异。

R2025a: `quadprog` 的 `ScaleProblem` 选项

quadprog 求解器的 "interior-point-convex" 算法增加了 ScaleProblem 选项，可加快某些缩放效果不佳的问题的求解速度。有关详细信息，请参阅 quadprog options 参量描述。

R2024b: 生成单精度代码

您可以使用 quadprog 为单精度浮点硬件生成代码。有关说明，请参阅单精度代码生成。

另请参阅

quadprog

语法

说明

示例

具有线性约束的二次规划

具有线性等式约束的二次规划

具有线性约束和边界的二次最小化

使用非默认选项的二次最小化

基于 prob2struct 的二次问题

返回 quadprog 目标函数值

检查 quadprog 优化过程

返回 quadprog 拉格朗日乘数

返回热启动对象

输入参数

H — 二次目标项 对称实矩阵

f — 线性目标项 实数向量

A — 线性不等式约束 实矩阵

b — 线性不等式约束 实数向量

Aeq — 线性等式约束 实矩阵

beq — 线性等式约束 实数向量

lb — 下界 实数向量 | 实数数组

ub — 上界 实数向量 | 实数数组

x0 — 初始点 实数向量

options — 优化选项 optimoptions 的输出 | 结构体，例如 optimset 返回的结构体

problem — 问题结构体 结构体

ws — 热启动对象 使用 optimwarmstart 创建的对象

输出参量

x — 解 实数向量

wsout — 热启动对象求解 QuadprogWarmStart 对象

fval — 解处的目标函数值 实数标量

exitflag — quadprog 停止的原因 整数

output — 有关优化过程的信息 结构体

lambda — 解处的拉格朗日乘数 结构体

详细信息

增强版退出消息

找到满足约束的最小值

求解器停滞，约束满足

问题似乎是无界问题

无法计算步进方向

此问题是非凸问题

预求解期间找到解

此问题不可行

此问题无界

收敛于不可行点

找不到可行的解

找不到可行的解

找到最佳解

找到最佳解

找到局部最小值

此问题无界

找到最佳解

可能是局部最小值

可能是局部最小值

退出消息的定义

容差

凸

可行方向

StepTolerance

OptimalityTolerance

有界问题的一阶最优性测度

ConstraintTolerance

相对对偶可行性

双重可行性

缩放因子

互补性测度

总相对误差

评价函数

预求解

问题似乎病态

算法

'interior-point-convex'

'trust-region-reflective'

'active-set'

热启动

替代功能

App

参考

扩展功能

C/C++ 代码生成 使用 MATLAB® Coder™ 生成 C 代码和 C++ 代码。

版本历史记录

基于 `prob2struct` 的二次问题

返回 `quadprog` 目标函数值

检查 `quadprog` 优化过程

返回 `quadprog` 拉格朗日乘数

`H` — 二次目标项
对称实矩阵

`f` — 线性目标项
实数向量

`A` — 线性不等式约束
实矩阵

`b` — 线性不等式约束
实数向量

`Aeq` — 线性等式约束
实矩阵

`beq` — 线性等式约束
实数向量

`lb` — 下界
实数向量 | 实数数组

`ub` — 上界
实数向量 | 实数数组

`x0` — 初始点
实数向量

`options` — 优化选项
`optimoptions` 的输出 | 结构体，例如 `optimset` 返回的结构体

`problem` — 问题结构体
结构体

`ws` — 热启动对象
使用 `optimwarmstart` 创建的对象

`x` — 解
实数向量

`wsout` — 热启动对象求解
`QuadprogWarmStart` 对象

`fval` — 解处的目标函数值
实数标量

`exitflag` — `quadprog` 停止的原因
整数

`output` — 有关优化过程的信息
结构体

`lambda` — 解处的拉格朗日乘数
结构体

`StepTolerance`

`OptimalityTolerance`

`ConstraintTolerance`

`'interior-point-convex'`

`'trust-region-reflective'`

`'active-set'`

C/C++ 代码生成
使用 MATLAB® Coder™ 生成 C 代码和 C++ 代码。

R2025a: `quadprog` 的 `ScaleProblem` 选项