optimproblem

创建优化问题

全页折叠

语法

prob = optimproblem
prob = optimproblem(Name,Value)

说明

使用 optimproblem 创建优化问题。

提示

有关完整的工作流，请参阅基于问题的优化工作流。

prob = optimproblem 用默认属性创建优化问题。

示例

prob = optimproblem(Name,Value) 使用一个或多个 Name,Value 对组参量指定的其他选项。例如，要指定最大化问题而不是最小化问题，请使用 prob = optimproblem('ObjectiveSense','maximize')。

注意

一个优化问题中的所有名称必须具有唯一性。具体来说，所有变量名称、目标函数名称和约束函数名称都不能相同。

示例

示例

全部折叠

打开实时脚本

使用默认属性创建优化问题。 

prob = optimproblem
prob = 
  OptimizationProblem with properties:

       Description: ''
    ObjectiveSense: 'minimize'
         Variables: [0×0 struct] containing 0 OptimizationVariables
         Objective: [0×0 OptimizationExpression]
       Constraints: [0×0 struct] containing 0 OptimizationConstraints

  No problem defined.
打开实时脚本

创建最大化线性规划问题。该问题有两个正变量和三个线性不等式约束。

prob = optimproblem('ObjectiveSense','max');

创建正变量。在问题中设置一个目标函数。

x = optimvar('x',2,1,'LowerBound',0);
prob.Objective = x(1) + 2*x(2);

在问题中创建线性不等式约束。

cons1 = x(1) + 5*x(2) <= 100;
cons2 = x(1) + x(2) <= 40;
cons3 = 2*x(1) + x(2)/2 <= 60;
prob.Constraints.cons1 = cons1;
prob.Constraints.cons2 = cons2;
prob.Constraints.cons3 = cons3;

检查此问题。

show(prob)
  OptimizationProblem : 

	Solve for:
       x

	maximize :
       x(1) + 2*x(2)


	subject to cons1:
       x(1) + 5*x(2) <= 100

	subject to cons2:
       x(1) + x(2) <= 40

	subject to cons3:
       2*x(1) + 0.5*x(2) <= 60

	variable bounds:
       0 <= x(1)
       0 <= x(2)

求解。

sol = solve(prob);
Solving problem using linprog.

Optimal solution found.

sol.x
ans = 2×1

    25
    15

此示例使用:

打开实时脚本

用二维变量 x 的两个目标函数创建一个问题。创建使用 x 的表达式作为目标函数，并将它们作为结构体放在目标中。

x = optimvar("x",2,LowerBound=-2,UpperBound=2);
prob = optimproblem;
prob.Objective.first = norm(x)^2;
prob.Objective.second = norm(x - [1;0])^2;

求解。

rng default % For reproducibility
sol = solve(prob);
Solving problem using gamultiobj.
gamultiobj stopped because the average change in the spread of Pareto solutions is less than options.FunctionTolerance.

绘制解。

paretoplot(sol)

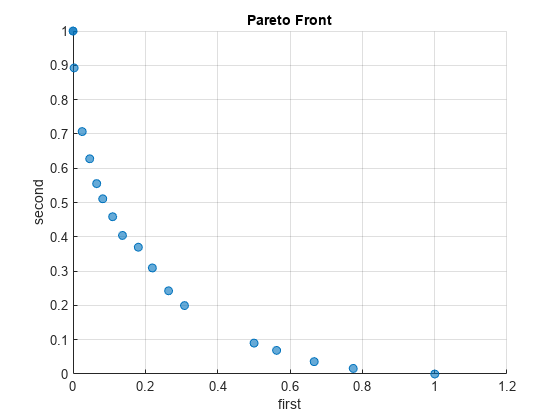
Figure contains an axes object. The axes object with title Pareto Front, xlabel first, ylabel second contains 4 objects of type text, scatter.

检查帕累托前沿的一个点。为此，请点击图窗，并点击数据提示工具：

datatips2.png

然后点击帕累托前沿上的一个点。

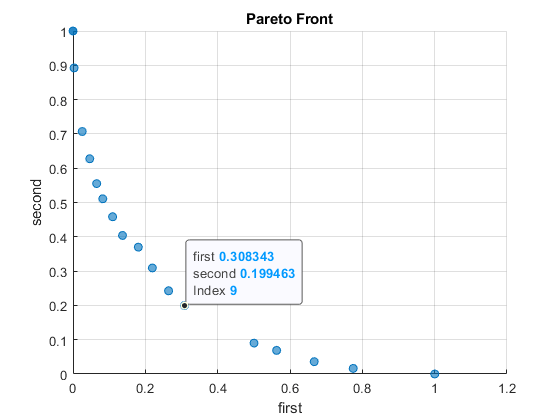
paretopoint.png

图中点的索引是 9。您可以找到与此点相关联的 x 值，作为索引为 9 的解。

sol(9).x
ans = 2×1

    0.5544
   -0.0306

名称-值参数

全部折叠

将可选参量对组指定为 Name1=Value1,...,NameN=ValueN，其中 Name 是参量名称，Value 是对应的值。名称-值参量必须出现在其他参量之后，但对各个参量对组的顺序没有要求。

在 R2021a 之前，使用逗号分隔每个名称和值，并用引号将 Name 引起来。

示例: 要指定最大化问题，请使用 prob = optimproblem('ObjectiveSense','maximize')。

问题约束，指定为 OptimizationConstraint 数组或以 OptimizationConstraint 数组为字段的结构体。

示例: prob = optimproblem('Constraints',sum(x,2) == 1)

问题标签，指定为字符串或字符向量。该软件不使用 Description 进行计算。Description 是任意标签，您可以将其用于任意目的。例如，您可以共享、存档或呈现模型或问题，并在 Description 中存储关于模型或问题的描述性信息。

示例: "An iterative approach to the Traveling Salesman problem"

数据类型: char | string

目标函数，指定为标量 OptimizationExpression 对象、OptimizationExpression 对象的数组或以标量 OptimizationExpression 作为字段的结构体。

  • 对于标量（单目标）问题，将目标函数指定为标量优化表达式或以标量优化表达式为值的结构体。

  • 对于多目标问题，将目标函数指定为向量值优化表达式、优化表达式数组或优化表达式结构体。例如，以下目标是包含以标量优化变量 x表示的优化表达式的结构体：

    prob = optimproblem;
prob.Objective.first = x^2;
prob.Objective.second = (x + 1)^2;

示例: prob = optimproblem('Objective',sum(sum(x)))（适用于二维变量 x）。

示例: prob = optimproblem('Objective',(x-a).^2)，其中 x 和 a 的大小为 2×1，x 是优化变量。

优化的意义，指定为 'minimize' 或 'maximize'。您还可以指定 'min' 以获得 'minimize' 或指定 'max' 以获得 'maximize'。当 ObjectiveSense 为 'minimize' 时，solve 函数将最小化目标；当 ObjectiveSense 为 'maximize' 时，函数将最大化目标。

ObjectiveSense 可以是具有 'minimize'、'min'、'maximize' 或 'max' 值的结构体。当问题目标是结构体时，可以使用这种形式。Objective 和 ObjectiveSense 结构体应具有相同的字段名称，因此 ObjectiveSense 适用于对应的 Objective。例如，

x = optimvar('x',2,"UpperBound",2,"LowerBound",-2);
prob = optimproblem;
prob.Objective.first = norm(x)^2;
prob.Objective.second = -norm(x - [1;0])^2;
prob.ObjectiveSense.first = "min";
prob.ObjectiveSense.second = "max";

如果 Objective 是结构体，您可以将 ObjectiveSense 指定为名称，例如 'max'。在这种情况下，所有目标都有相同的 ObjectiveSense。

示例: prob = optimproblem('ObjectiveSense','max')

数据类型: char | string

输出参量

全部折叠

优化问题，以 OptimizationProblem 对象形式返回。通常，要完成问题描述，您需要指定目标函数和约束。但是，您可能会遇到没有目标函数的可行性问题，或遇到没有约束的问题。通过调用 solve 求解完整的问题。

警告

基于问题的方法不支持在目标函数、非线性等式和非线性不等式中使用复数值。如果某函数计算具有复数值，即使是作为中间值，最终结果也可能不正确。

版本历史记录

在 R2017b 中推出

另请参阅

| |

主题