最小二乘(模型拟合)算法
最小二乘定义
一般情况下,最小二乘问题求的是作为某一函数局部最小值点的向量 x,函数具有平方和的形式,求解可能需要满足一定的约束:
满足 A·x ≤ b, Aeq·x = beq, lb ≤ x ≤ ub, c(x) ≤ 0, ceq(x) = 0。
线性最小二乘问题是:给定矩阵 C 和向量 d,求出满足边界和线性约束的最小化 ‖Cx – d‖2 的 x。
Optimization Toolbox™ 提供几种求解器,适用于各种类型的 F(x) 和各种类型的约束:
| 求解器 | F(x) | 约束 |
|---|---|---|
mldivide | C·x – d | 无 |
lsqnonneg | C·x – d | x ≥ 0 |
lsqlin | C·x – d | 边界、线性 |
lsqnonlin | 一般形式的 F(x) | 一般的线性和非线性 |
lsqcurvefit | F(x, xdata) – ydata | 一般的线性和非线性 |
除了 mldivide 中使用的算法外,Optimization Toolbox 求解器中还有六种最小二乘算法:
除 lsqlin 活动集外,其他所有算法都可以使用稀疏数据;请参阅稀疏性在优化算法中的应用。有关非线性最小二乘方法的一般概况,请参阅 Dennis 的论著 [8]。莱文贝格-马夸特方法的具体细节可见于 Moré 的论著 [28]。
对于没有约束的线性最小二乘,问题可以表示为要求出问题 Cx = d 的最小二乘解。您可以使用 mldivide 或 lsqminnorm 来求解此问题。当问题具有线性或边界约束时,请使用 lsqlin。对于一般非线性约束,请使用 lsqnonlin。
线性最小二乘:内点或活动集
lsqlin 'interior-point' 算法使用 interior-point-convex quadprog 算法,lsqlin 'active-set' 算法使用活动集 quadprog 算法。quadprog 问题定义用于最小化以下二次函数
且需要满足线性约束和边界约束。lsqlin 函数在满足线性约束和边界约束的前提下最小化向量 Cx – d 的 2-范数平方。换句话说,lsqlin 最小化下式
将上式的 2CTC 替换为 H 矩阵,并将 (–2CTd) 替换为 c 向量,即符合 quadprog 框架。(加法项 dTd 对最小值的位置没有影响。)在重新表示 lsqlin 问题后,quadprog 会计算解。
信赖域反射最小二乘
信赖域反射最小二乘算法
Optimization Toolbox 求解器中使用的许多方法都基于信赖域,这是一个简单而功能强大的优化概念。
要理解信赖域优化方法,请考虑无约束最小化问题,最小化 f(x),该函数接受向量参量并返回标量。假设您现在位于 n 维空间中的点 x 处,并且您要寻求改进,即移至函数值较低的点。基本思路是用较简单的函数 q 来逼近 f,该函数需能充分反映函数 f 在点 x 的邻域 N 中的行为。此邻域是信赖域。试探步 s 是通过在 N 上进行最小化(或近似最小化)来计算的。以下是信赖域子问题,
| (1) |
如果 f(x + s) < f(x),当前点更新为 x + s;否则,当前点保持不变,信赖域 N 缩小,算法再次计算试探步。
在定义特定信赖域方法以最小化 f(x) 的过程中,关键问题是如何选择和计算逼近 q(在当前点 x 上定义)、如何选择和修改信赖域 N,以及如何准确求解信赖域子问题。本节重点讨论无约束问题。后面的章节讨论由于变量约束的存在而带来的额外复杂性。
在标准信赖域方法 ([48]) 中,二次逼近 q 由 F 在 x 处的泰勒逼近的前两项定义;邻域 N 通常是球形或椭圆形。以数学语言表述,信赖域子问题通常写作
| (2) |
其中,g 是 f 在当前点 x 处的梯度,H 是黑塞矩阵(二阶导数的对称矩阵),D 是对角缩放矩阵,Δ 是正标量,‖ . ‖ 是 2-范数。存在求解公式 2 的好算法(请参阅[48]);此类算法通常涉及计算 H 的所有特征值,并将牛顿法应用于以下久期方程
此类算法提供公式 2 的精确解。但是,它们要耗费与 H 的几个分解成比例的时间。因此,对于信赖域问题,需要采取另一种方法。文献([42] 和 [50])中提出了几种基于公式 2 的逼近和启发式方法建议。Optimization Toolbox 求解器采用的逼近方法是将信赖域子问题限制在二维子空间 S 内([39] 和 [42])。一旦计算出子空间 S,即使需要完整的特征值/特征向量信息,求解公式 2 的工作量也不大(因为在子空间中,问题只是二维的)。现在的主要工作已转移到子空间的确定上。
二维子空间 S 是借助下述预条件共轭梯度法确定的。求解器将 S 定义为由 s1 和 s2 确定的线性空间,其中 s1 是梯度 g 的方向,s2 是近似牛顿方向,即下式的解
| (3) |
或是负曲率的方向,
| (4) |
以此种方式选择 S 背后的理念是强制全局收敛(通过最陡下降方向或负曲率方向)并实现快速局部收敛(通过牛顿步,如果它存在)。
现在,我们可以很容易地给出基于信赖域的无约束最小化的大致框架:
构造二维信赖域子问题。
求解公式 2 以确定试探步 s。
如果 f(x + s) < f(x),则 x = x + s。
调整 Δ。
重复这四个步骤,直到收敛。信赖域维度 Δ 根据标准规则进行调整。具体来说,它会在试探步不被接受(即 f(x + s) ≥ f(x))时减小。有关这方面的讨论,请参阅[46] 和 [49]。
Optimization Toolbox 求解器用专用函数处理 f 的一些重要特例:非线性最小二乘、二次函数和线性最小二乘。然而,其底层算法思路与一般情况相同。这些特例将在后面的章节中讨论。
大规模非线性最小二乘
f(x) 的一个重要特例是非线性最小二乘问题
| (5) |
其中,F(x) 是向量值函数,F(x) 的分量 i 等于 fi(x)。用于求解此问题的基本方法与非线性最小化信赖域方法中所述的一般情况相同。不过,我们可以充分利用非线性最小二乘问题的结构来提高效率。具体来说,就是使用近似高斯-牛顿方向,即下式的解 s
| (6) |
(其中 J 是 F(x) 的雅可比矩阵)来定义二维子空间 S。此处不使用分量函数 fi(x) 的二阶导数。
每次迭代中,算法都使用预条件共轭梯度法来近似求解标准方程,即,
(虽然并不显式构造标准方程)。
大规模线性最小二乘
在这种情况下,要求解的函数 f(x) 是
可能需要满足线性约束。算法生成严格可行的迭代,在极限情况下收敛于局部解。每次迭代都涉及大型线性系统的近似解(阶数为 n,其中 n 是 x 的长度)。迭代矩阵具有矩阵 C 的结构。具体来说,算法使用预条件共轭梯度法来近似求解标准方程,即,
(虽然并不显式构造标准方程)。
此处使用子空间信赖域方法来确定搜索方向。然而,它不采用非线性最小化情形中的做法,将步限制为(可能)一个反射步,而是采用二次情形中的做法,在每次迭代中进行分段反射线搜索。请参阅[45] 了解线搜索的详细信息。最终,这些线性系统表示一种牛顿法,该方法在解处捕获一阶最优性条件,实现快速局部收敛。
雅可比矩阵乘法函数. lsqlin 无需显式构造矩阵 C 即可求解线性约束最小二乘问题。它使用雅可比矩阵乘法函数 jmfun,
W = jmfun(Jinfo,Y,flag)
(该函数由您提供。)该函数必须计算矩阵 Y 的下列乘积:
如果
flag == 0,则W = C'*(C*Y)。如果
flag > 0,则W = C*Y。如果
flag < 0,则W = C'*Y。
如果 C 很大,但其包含的结构足以让您在不显式构造 C 的情况下编写 jmfun,这种函数将非常有用。有关示例,请参阅雅可比乘法函数与线性最小二乘法。
莱文贝格-马夸特方法
最小二乘问题对平方和函数 f(x) 进行最小化。
| (7) |
这种类型的问题出现在大量的实际应用中,特别是涉及对数据进行模型函数拟合(如非线性参数估计)的应用中。这种问题类型也出现在下面这类控制系统中:对于向量 x 和标量 t,其目标是输出 y(x,t) 遵循连续模型轨迹 φ(t)。此问题可以表达为
| (8) |
其中 y(x,t) 和 φ(t) 是标量函数。
对积分进行离散化以获得逼近
| (9) |
其中 ti 是等间距的。在此问题中,向量 F(x) 为
在这类问题中,最优情形下的残差 ‖F(x)‖ 可能很小,因为通常的做法是设置现实可行的目标轨迹。虽然可以使用一般的无约束最小化方法来最小化公式 7中的函数(如无约束优化的基础知识中所述),但问题的某些特征经常可以被用来提高求解过程的迭代效率。公式 7 的梯度和黑塞矩阵具有特殊结构。
将 F(x) 的 m×n 雅可比矩阵表示为 J(x),f(x) 的梯度向量表示为 G(x),f(x) 的黑塞矩阵表示为 H(x),并将每个 Fi(x) 的黑塞矩阵表示为 Di(x),
| (10) |
其中
矩阵 Q(x) 的一个属性是:当残差 ‖F(x)‖ 随着 xk 接近解而趋于零时,Q(x) 也趋于零。因此,当解处的 ‖F(x)‖ 很小时,一个高效方法是使用高斯-牛顿方向作为优化过程的基础。
在每次主迭代 k 中,高斯-牛顿法都会得到一个搜索方向 dk,该方向是线性最小二乘问题的解
| (11) |
当 Q(x) = 0 时,从该方法推导出的方向等效于牛顿方向。算法可将搜索方向 dk 作为线搜索策略的一部分,以确保在每次迭代中函数 f(x) 会减小。
当二阶项 Q(x) 不可忽略时,高斯-牛顿法经常遇到问题。莱文贝格-马夸特方法能够克服此问题。
莱文贝格-马夸特方法(请参阅 [25] 和 [27])使用的搜索方向是以下线性方程组的解
| (12) |
也可以是以下方程的解
| (13) |
其中标量 λk 控制 dk 的幅值和方向,而 diag(A) 表示 A 中对角项的矩阵。将选项 ScaleProblem 设置为 'none' 以选择公式 12,或将 ScaleProblem 设置为 'Jacobian' 以选择公式 13。
您可以使用 InitDamping 选项设置参数 λ0 的初始值。个别情况下,此选项的默认值 0.01 可能不合适。如果您发现莱文贝格-马夸特算法的初始进展甚微,请尝试将 InitDamping 设置为不同于默认值的值(例如 1e2)。
当 λk 为零时,方向 dk 与高斯-牛顿法的方向相同。随着 λk 趋向于无穷,dk 趋向于最陡下降方向,模趋向于零。因此,对于一些足够大的 λk,项 ‖ F(xk + dk)‖ < ‖ F(xk)‖ 成立,其中 ‖ 表示欧几里德范数。因此,即便算法遇到二阶项而对高斯-牛顿法的效率造成限制,您仍能控制项 λk 以确保下降。当步成功(给出较低的函数值)时,该算法设置 λk+1 = λkλk/10。当步不成功时,该算法设置 λk+1 = λk*10。
莱文贝格-马夸特算法在内部使用最优性容差(停止条件)1e-4 乘以函数容差。
因此,莱文贝格-马夸特方法使用的搜索方向综合了高斯-牛顿方向和最陡下降方向。
莱文贝格-马夸特方法的另一项优势体现在当雅可比矩阵 J 秩亏时。在这种情况下,高斯-牛顿法可能会有数值问题,因为 公式 11 中的最小化问题不适定。相反,莱文贝格-马夸特方法在每次迭代中都有满秩,因此可避免这些问题。
下图显示莱文贝格-马夸特方法在最小化罗森布罗克函数时的迭代,这是众所周知的以最小二乘法形式出现的最小化难题。
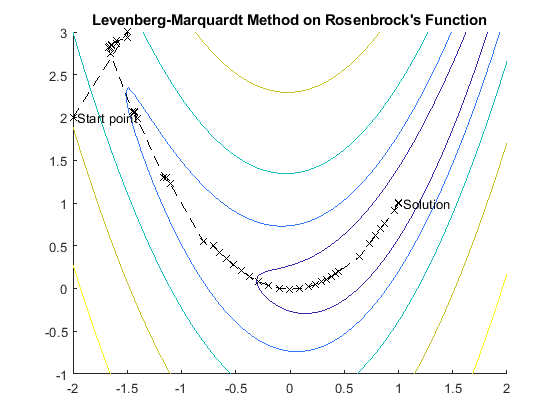
有关此图窗的更完整描述,请参阅香蕉函数的最小化。
莱文贝格-马夸特方法中的边界约束
当问题包含边界约束时,lsqcurvefit 和 lsqnonlin 会修改莱文贝格-马夸特迭代。如果建议的迭代点 x 位于边界之外,算法会将该步投影到最近的可行点上。换句话说,在 P 定义为将不可行点投影到可行域上的投影算子的情况下,算法会将建议的点 x 修改为 P(x)。根据定义,投影算子 P 根据以下条件独立地对每个分量 xi 进行运算
或者采用以下等效命令,
该算法修改一阶最优性测度的停止条件。假设 x 是建议的迭代点。在无约束情况下,停止条件为
| (14) |
其中 tol 是最优性容差值,为 1e-4*FunctionTolerance。在有界情况下,停止条件是
| (15) |
要理解此条件,首先要注意,如果 x 在可行域的内部,则算子 P 不起作用。因此,终止条件变为
这与原始的无约束停止条件 相同。如果边界约束处于活动状态,这意味着 x – ∇f(x) 不可行,则在算法应停止的点上,边界上某点的梯度垂直于边界。因此,点 x 等于最陡下降步长的投影 P(x – ∇f(x)),如下图所示。
莱文贝格-马夸特停止条件
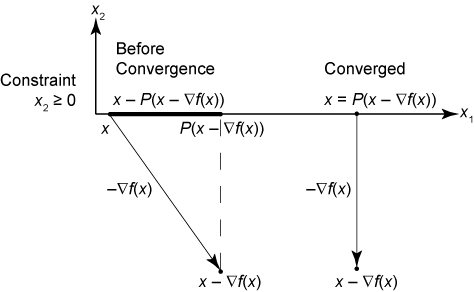
针对约束最小二乘修正的 fmincon 算法
为了处理线性和非线性约束,lsqnonlin 和 lsqcurvefit 求解器的 'interior-point' 算法会在内部调用 fmincon 'interior-point' 算法的修正版本。该修正版本使用的黑塞矩阵逼近不同于运行 fmincon 时使用的黑塞矩阵逼近。默认情况下,fmincon 使用 BFGS 黑塞矩阵逼近。在本节后面,您可以找到最小二乘求解器使用的不同黑塞矩阵逼近。有关 fmincon 'interior-point' 算法及其黑塞矩阵逼近的详细信息,请参阅 fmincon 内点算法。
在最小二乘法的上下文中,目标函数 f(x) 是向量,而不是标量。要最小化的平方和为
fT(x)f(x).
要求解的问题是
使得
c(x) ≤ 0
ceq(x) = 0.
此问题的拉格朗日函数是
关于拉格朗日函数的 x 的梯度为
此处,F 是目标函数的雅可比矩阵
而 AE 和 AI 分别是等式约束函数 ceq(x) 和不等式约束函数 c(x) 的雅可比矩阵。
该问题的卡鲁什-库恩-塔克 (KKT) 条件是
此处,变量 s 和 λI 为非负值,S = diag(s),μ 是随着迭代次数的增加而趋于零的障碍参数,e 是由 1 组成的向量。
为了求解这些方程,软件会执行迭代。调用迭代序号 k。此算法尝试通过使用以下更新方程执行步 Δx、Δs、ΔλE、ΔλI 来求解这些方程:
此处,H 是目标函数的黑塞矩阵。使用 BFGS·黑塞矩阵逼近,步骤 k + 1 处的逼近黑塞矩阵 Bk +1 为
| (16) |
其中
此黑塞矩阵逼近的初始值是 B0 = I。
有关 fmincon 中这种方法的讨论,请参阅更新黑塞矩阵。
与 fmincon 黑塞矩阵更新相比,最小二乘 BFGS 黑塞矩阵更新存在以下差异。最小二乘目标函数的黑塞矩阵是
最小二乘黑塞矩阵更新使用首项 2FTF 作为单独的量,并使用不带 2FTF 项的 BFGS 公式更新黑塞矩阵逼近。换句话说,BFGS 黑塞矩阵更新使用黑塞矩阵更新公式公式 16 作为 Bk,其中拉格朗日函数的黑塞逼近(目标函数加上拉格朗日乘数乘以约束)是 2FTF + Bk,并且量 sk 和 yk 是
| (17) |
这种修正的黑塞矩阵逼近方法解释了针对同一问题 fmincon 迭代与 lsqnonlin 或 lsqcurvefit 迭代之间的差异。在内部,最小二乘求解器使用黑塞矩阵逼近公式 16 和公式 17 作为 fmincon 求解器中的自定义黑塞函数。
另请参阅
quadprog | lsqlin | lsqcurvefit | lsqnonlin | lsqnonneg
