约束非线性优化算法
约束优化定义
约束最小化问题求向量 x,在满足 x 取值约束的前提下,使得标量函数 f(x) 取得局部最小值:
使得以下一项或多项成立:c(x) ≤ 0, ceq(x) = 0, A·x ≤ b, Aeq·x = beq, l ≤ x ≤ u。半无限规划会使用更多约束;请参阅 fseminf 问题的表示和算法。
fmincon 信赖域反射算法
非线性最小化信赖域方法
Optimization Toolbox™ 求解器中使用的许多方法都基于信赖域,这是一个简单而功能强大的优化概念。
要理解信赖域优化方法,请考虑无约束最小化问题,最小化 f(x),该函数接受向量参量并返回标量。假设您现在位于 n 维空间中的点 x 处,并且您要寻求改进,即移至函数值较低的点。基本思路是用较简单的函数 q 来逼近 f,该函数需能充分反映函数 f 在点 x 的邻域 N 中的行为。此邻域是信赖域。试探步 s 是通过在 N 上进行最小化(或近似最小化)来计算的。以下是信赖域子问题,
| (1) |
如果 f(x + s) < f(x),当前点更新为 x + s;否则,当前点保持不变,信赖域 N 缩小,算法再次计算试探步。
在定义特定信赖域方法以最小化 f(x) 的过程中,关键问题是如何选择和计算逼近 q(在当前点 x 上定义)、如何选择和修改信赖域 N,以及如何准确求解信赖域子问题。本节重点讨论无约束问题。后面的章节讨论由于变量约束的存在而带来的额外复杂性。
在标准信赖域方法 ([48]) 中,二次逼近 q 由 F 在 x 处的泰勒逼近的前两项定义;邻域 N 通常是球形或椭圆形。以数学语言表述,信赖域子问题通常写作
| (2) |
其中,g 是 f 在当前点 x 处的梯度,H 是黑塞矩阵(二阶导数的对称矩阵),D 是对角缩放矩阵,Δ 是正标量,‖ . ‖ 是 2-范数。存在求解公式 2 的好算法(请参阅[48]);此类算法通常涉及计算 H 的所有特征值,并将牛顿法应用于以下久期方程
此类算法提供公式 2 的精确解。但是,它们要耗费与 H 的几个分解成比例的时间。因此,对于大型问题,需要一种不同方法。文献([42] 和 [50])中提出了几种基于公式 2 的逼近和启发式方法建议。Optimization Toolbox 求解器采用的逼近方法是将信赖域子问题限制在二维子空间 S 内([39] 和 [42])。一旦计算出子空间 S,即使需要完整的特征值/特征向量信息,求解公式 2 的工作量也不大(因为在子空间中,问题只是二维的)。现在的主要工作已转移到子空间的确定上。
二维子空间 S 是借助下述预条件共轭梯度法确定的。求解器将 S 定义为由 s1 和 s2 确定的线性空间,其中 s1 是梯度 g 的方向,s2 是近似牛顿方向,即下式的解
| (3) |
或是负曲率的方向,
| (4) |
以此种方式选择 S 背后的理念是强制全局收敛(通过最陡下降方向或负曲率方向)并实现快速局部收敛(通过牛顿步,如果它存在)。
现在,我们可以很容易地给出基于信赖域的无约束最小化的大致框架:
构造二维信赖域子问题。
求解公式 2 以确定试探步 s。
如果 f(x + s) < f(x),则 x = x + s。
调整 Δ。
重复这四个步骤,直到收敛。信赖域维度 Δ 根据标准规则进行调整。具体来说,它会在试探步不被接受(即 f(x + s) ≥ f(x))时减小。有关这方面的讨论,请参阅[46] 和 [49]。
Optimization Toolbox 求解器用专用函数处理 f 的一些重要特例:非线性最小二乘、二次函数和线性最小二乘。然而,其底层算法思路与一般情况相同。这些特例将在后面的章节中讨论。
预条件共轭梯度法
求解大型对称正定线性方程系统 Hp = –g 的一种常用方法是预条件共轭梯度法 (PCG)。这种迭代方法需要能够计算 H·v 形式的矩阵-向量积,其中 v 是任意向量。对称正定矩阵 M 是 H 的预条件子。也就是说,M = C2,其中 C–1HC–1 是良态矩阵或具有聚类特征值的矩阵。
在最小化上下文中,您可以假设黑塞矩阵 H 是对称矩阵。然而,只有在强最小值点的邻域内才能保证 H 是正定矩阵。算法 PCG 在遇到负(或零)曲率方向(即 dTHd ≤ 0)时退出。PCG 输出方向 p 要么是负曲率方向,要么是牛顿方程组 Hp = –g 的近似解。无论哪种情况,p 都有助于定义在非线性最小化信赖域方法中讨论的信赖域方法中使用的二维子空间。
线性等式约束
线性约束使无约束最小化中所述的情形复杂化了。不过,我们仍可以简洁高效地沿用前述的基本思路。Optimization Toolbox 求解器中的信赖域方法生成严格可行的迭代。
一般的线性等式约束最小化问题可以写作
| (5) |
其中 A 是 m×n 矩阵 (m ≤ n)。一些 Optimization Toolbox 求解器对 A 进行预处理,以使用基于 AT 的 LU 分解的方法来消除严格的线性相关性 [46]。此处假定 A 的秩为 m。
用于求解公式 5 的方法在两个重要方面不同于无约束方法。首先,它使用稀疏最小二乘步计算初始可行点 x0,满足 Ax0 = b。然后,它用简化的预条件共轭梯度 (RPCG) 代替算法 PCG(请参阅[46]),以便计算近似的简化牛顿步(或 A 的零空间中的负曲率方向)。关键的线性代数步涉及求解以下形式的方程组
| (6) |
其中, 逼近 A(在不丢失秩的前提下,A 的小非零值会设置为零)且 C 是 H 的稀疏对称正定逼近,即 C = H。有关详细信息,请参阅[46]。
框约束
框约束问题具有以下形式
| (7) |
其中,l 是由下界组成的向量,u 是由上界组成的向量。l 的部分(或全部)分量可以等于 –∞,u 的部分(或全部)分量可以等于 ∞。该方法生成一系列严格可行点。此处用到了两种技巧,在保持可行性的同时实现稳健的收敛行为。其一,用缩放的修正牛顿步取代无约束牛顿步(以定义二维子空间 S)。其次,反射用于增大步长。
缩放的修正牛顿步源于对公式 7 的库恩-塔克必要条件的检验,
| (8) |
其中
对于每个 1 ≤ i ≤ n,向量 v(x) 定义如下:
如果 gi < 0 且 ui < ∞,则 vi = xi – ui
如果 gi ≥ 0 且 li > –∞,则 vi = xi – li
如果 gi < 0 且 ui = ∞,则 vi = –1
如果 gi ≥ 0 且 li = –∞,则 vi = 1
非线性系统公式 8 不是处处可微的。不可微分性发生在 vi = 0 时。您可以通过保持严格的可行性(例如限制 l < x < u)来避免这些不可微分的点。
公式 8 给出的非线性系统的缩放的修正牛顿步 sk 定义为以下线性系统的解
| (9) |
在第 k 次迭代中的解,其中
| (10) |
并且
| (11) |
在此处,Jv 表示 |v| 的雅可比。对角矩阵 Jv 的每个对角分量等于 0、–1 或 1。如果 l 和 u 的所有分量均为有限的,则 Jv = diag(sign(g))。在满足 gi = 0 的点上,vi 可能不可微分。 在此类点上定义。这种类型的不可微分性不值得关注,因为对于这种分量,vi 采用哪个值并不重要。此外,|vi| 在此点上仍是不连续的,但函数 |vi|·gi 是连续的。
其次,反射用于增大步长。单个反射步定义如下。给定与边界约束相交的步 p,假设与 p 相交的第一个边界约束是第 i 个边界约束(可以是第 i 个上界,也可以是第 i 个下界),则反射步 pR = p,但在第 i 个分量中除外,其中 pRi = –pi。
fmincon 活动集算法
简介
在约束优化中,一般目标是将问题转换为更容易的子问题,然后对子问题求解并将其用作迭代过程的基础。一大类早期方法的特点是通过对约束边界附近或之外的约束使用罚函数,从而将约束问题转换为基本的无约束问题。通过这种方式,使用参数化的无约束优化的序列来求解约束问题,这些优化在(序列的)极限内收敛于约束问题。这些方法现在认为是相对低效的,已被重点求解卡鲁什-库恩-塔克 (KKT) 方程的方法所取代。KKT 方程是约束优化问题的最优性的必要条件。如果问题是所谓的凸规划问题,即 f(x) 和 Gi(x), i = 1,...,m 是凸函数,则 KKT 方程对于全局解点既必要又充分。
参考 GP (公式 1),库恩-塔克方程可表述为
| (12) |
(此外还包括公式 1 中的原始约束)。
第一个方程说明取消在解点处目标函数和活动约束之间的梯度。对于要取消的梯度,拉格朗日乘数(λi,i = 1、...、m)是平衡目标函数和约束梯度的模偏差的必要条件。由于该取消操作仅包含活动约束,不活动约束不能包含在该操作中,因此给定的拉格朗日乘数等于 0。这在最后两个库恩-塔克方程中以隐式表述。
KKT 方程的解构成许多非线性规划算法的基础。这些算法尝试直接计算拉格朗日乘数。约束拟牛顿法通过使用拟牛顿更新过程累积关于 KKT 方程的二阶信息来保证超线性收敛。这些方法通常称为序列二次规划 (SQP) 方法,因为每个主迭代都求解一个 QP 子问题(也称为迭代二次规划、递归二次规划或约束变量度量法)。
'active-set' 算法不能使用稀疏数据;请参阅稀疏性在优化算法中的应用。
序列二次规划 (SQP)
SQP 方法呈现了非线性规划方法的最新进展。例如,席特科夫斯基[36] 已实现并测试了一个版本,对于大量测试问题,该版本在效率、准确度和成功解的百分比方面优于所有其他经过测试的方法。
基于比格斯[1]、汉Han [22] 和鲍威尔([32] 及 [33])的工作,该方法允许您在处理约束优化问题时高度模拟牛顿法,就像在处理无约束优化问题时一样。在每个主迭代中,使用拟牛顿更新方法逼近拉格朗日函数的黑塞矩阵。然后使用该矩阵生成 QP 子问题,其解构成线搜索过程的搜索方向。有关 SQP 的概述,请参阅弗莱彻的论著 [13]、吉尔等人的论著 [19]、鲍威尔的论著 [35] 和席特科夫斯基的论著 [23]。此处将说明一般方法。
针对 GP (公式 1) 中的问题描述,核心思路是基于拉格朗日函数的二次逼近来构造 QP 子问题。
| (13) |
在这里,您假设边界约束已表示为不等式约束,从而简化公式 1。通过线性化非线性约束,您可以得到 QP 子问题。
二次规划 (QP) 子问题
| (14) |
此子问题可以用任何 QP 算法来求解(有关实例,请参阅二次规划解)。该解用于形成新迭代
xk + 1 = xk + αkdk。
步长参数 αk 由适当的线搜索过程确定,以便在评价函数中获得充分的降幅(请参阅更新黑塞矩阵)。矩阵 Hk 是拉格朗日函数的黑塞矩阵的正定逼近(公式 13)。Hk 可以通过任何拟牛顿法进行更新,不过最常用的仍是 BFGS 方法(请参阅更新黑塞矩阵)。
使用 SQP 时,相比无约束问题,非线性约束问题通常可以用更少的迭代次数完成求解。其中一个原因是,由于可行区域的限制,优化器可以就搜索方向和步长作出明智的决定。
假设有罗森布罗克函数 g(x),它有一个额外的非线性不等式约束,如下所示,
| (15) |
使用 SQP 实现可在 31 次迭代后求解该问题,而对于无约束情形则需要 37 次迭代。图窗显示从 x = [–1.9,2.0] 开始的解点 x = [0.9072,0.8228] 的路径。
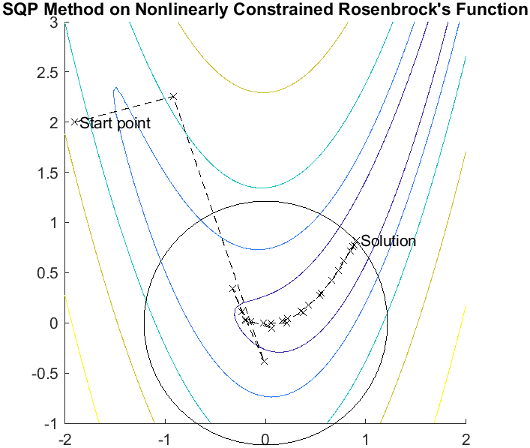
SQP 实现
SQP 实现由三个主要阶段组成,以下各小节将对它们进行简要讨论:
更新黑塞矩阵. 在每次主迭代中,拉格朗日函数的黑塞矩阵的正定拟牛顿逼近 H 使用 BFGS 方法进行计算,其中 λi, i = 1,...,m 是拉格朗日乘数的估计值。
| (16) |
其中
鲍威尔[33] 建议保持黑塞矩阵为正定,即使它在解点处可能是正不定的。如果 在每次更新时都为正,并且 H 用正定矩阵进行初始化,则黑塞矩阵保持正定。当 为非正时,qk 将逐元素进行修正,使得 。这种修正的总体目标是使 qk 的元素的失真尽可能少,这些元素有助于正定更新。因此,在修正的初始阶段,qk*sk 的最负元素会重复减半。此过程一直持续到 大于或等于一个小的负容差。如果在此过程后 仍不是正的,请通过添加向量 v 乘以常量标量 w 来修正 qk,即,
| (17) |
其中
并系统地增大 w,直到 变为正。
函数 fmincon、fminimax、fgoalattain 和 fseminf 都使用 SQP。如果在 options 中 Display 设置为 'iter',则会给出各种信息,如函数值和最大约束违反值。如果必须使用上述过程的第一阶段对黑塞矩阵进行修正以使其保持正定,则将显示 Hessian modified。如果必须使用上述方法的第二阶段再次修正黑塞矩阵,则将显示 Hessian modified twice。当 QP 子问题不可行时,将显示 infeasible。这种显示通常不需要格外关注,但它们表明问题是高度非线性的,收敛可能比平时需要更长时间。有时会显示消息 no update,表明 几乎为零。这可能表明问题设置错误,或您尝试最小化不连续函数。
二次规划解. 在 SQP 方法的每个主迭代中,都会求解一个以下形式的 QP 问题,其中 Ai 指 m×n 矩阵 A 的第 i 行。
| (18) |
Optimization Toolbox 函数使用的方法是一种活动集策略(也称为投影方法),类似于吉尔等人在 [18] 和 [17] 中所述的策略。它经过了修正,对线性规划 (LP) 和二次规划 (QP) 问题都适用。
求解过程包括两个阶段。第一阶段包括计算一个可行点(如果存在)。第二阶段包括生成可行点的迭代序列,这些可行点收敛于解。在此方法中,保持活动集 ,该活动集是对在解点处的活动约束(即约束边界上的约束)的估计值。几乎所有 QP 算法均为活动集方法。之所以强调这一点,是因为存在许多不同方法,它们在结构上非常相似,但在描述上千差万别。
在每个迭代 k 中都会得到更新,它构成搜索方向 的基础。等式约束始终维持在活动集 中。此处将变量写作 ,以区别于 SQP 方法主迭代中的 dk。计算搜索方向 以最小化目标函数,同时确保该方向位于活动约束边界上。 的可行子空间基于 Zk 而形成,其列与活动集 的估计值(例如 )正交。这就确保了搜索方向(由 Zk 的列的任意组合经线性求和形成)始终位于活动约束的边界上。
矩阵 Zk 由矩阵 的 QR 分解的最后 m – l 个列组成,其中 l 是活动约束的数量且 l < m。也就是说,Zk 由下式给出
| (19) |
其中
一旦找到 Zk,就会寻找使 q(d) 最小化的新搜索方向 , 位于活动约束的零空间中。也就是说, 是 Zk 的列的线性组合:对于某个向量 p,。
这样,如果您将二次函数视为 p 的函数,通过代换 ,您就得到
| (20) |
求上式关于 p 的微分,可得
| (21) |
∇q(p) 称为二次函数的投影梯度,因为它是投影到 Zk 定义的子空间中的梯度。项 称为投影黑塞矩阵。假设黑塞矩阵 H 是正定矩阵(在此 SQP 实现中就是如此),则函数 q(p) 在 Zk 定义的子空间中的最小值出现在 ∇q(p) = 0 处,即以下线性方程系统的解
| (22) |
然后采取以下形式的步
| (23) |
在每次迭代中,因为目标函数的二次性质,步长 α 只有两种选择。沿 的单位步是 的零空间内到函数最小值的精确步。如果能够在不违反约束的情况下采取此步,则这就是 QP(公式 18)的解。否则,沿 到最近约束的步小于单位步,并且下一次迭代时,活动集中将加入一个新的约束。沿任一方向 到约束边界的距离由下式给出
| (24) |
该定义针对不在活动集中的约束,其中的方向 朝向约束边界,即 。
如果活动集中包含 n 个独立约束,且最小值的位置未知,则会计算满足以下非奇异线性方程组的拉格朗日乘数 λk
| (25) |
如果 λk 的所有元素均为正,则 xk 是 QP (公式 18) 的最优解。但是,如果 λk 的任一分量为负,并且该分量不对应于等式约束,则从活动集中删除对应的元素并寻找新迭代。
初始化. 算法需要一个可行的起点。如果 SQP 方法提供的当前点不可行,则您可以通过求解线性规划问题找到一个点
| (26) |
Ai 表示矩阵 A 中的第 i 行。通过将 x 设置为满足等式约束的值,您可以找到公式 26 的一个可行点(如果存在)。您可以通过求解由等式约束形成的欠定或超定线性方程组来确定该值。如果存在此问题的解,则松弛变量 γ 设置为在此点的最大不等式约束。
您可以通过将每次迭代中的搜索方向设置为最陡下降方向来修正前述 QP 算法以用于 LP 问题,其中 gk 是目标函数的梯度(等于线性目标函数的系数)。
| (27) |
如果使用上述 LP 方法找到一个可行点,则进入主 QP 阶段。使用求解以下线性方程组得到的搜索方向 来初始化搜索方向
| (28) |
其中,gk 是当前迭代 xk(即 Hxk + c)中目标函数的梯度。
如果没有找到 QP 问题的可行解,则选取使 γ 最小化的方向作为主 SQP 例程 的搜索方向。
线搜索和评价函数. QP 子问题的解生成向量 dk,该向量用于形成新迭代
| (29) |
确定适当的步长参数 αk,以在评价函数中产生充分的降幅。在此实现中使用以下形式的评价函数(参考 Han 的论著 [22] 和鲍威尔的论著 [33])。
| (30) |
鲍威尔建议设置罚参数
| (31) |
这使得在 QP 解中为非活动但近期曾经活动的约束能够作出正的贡献。在此实现中,罚参数 ri 初始设置为
| (32) |
其中 表示欧几里德范数。
这可以确保具有较小梯度的约束对罚参数的贡献更大,在解点处的活动约束即属此种情况。
fmincon SQP 算法
sqp 算法(以及与之几乎相同的 sqp-legacy 算法)与 active-set 算法类似(有关说明,请参阅fmincon 活动集算法)。基本的 sqp 算法在 Nocedal 和 Wright 的 [31] 的第 18 章中进行了介绍。
sqp 算法与 sqp-legacy 算法基本相同,但实现方式不同。通常来说,与 sqp-legacy 相比,sqp 的执行时间更短,内存使用量更少。
sqp 和 active-set 算法之间最重要的区别是:
关于边界的严格可行性
sqp 算法在受边界约束的区域内执行每个迭代步。此外,有限差分步也遵守边界。边界并不严格;步可以正好位于边界上。当目标函数或非线性约束函数在受边界约束的区域之外未定义或者为复数时,这种严格的可行性是有益的。
非双精度值结果的稳健性
在迭代过程中,sqp 算法尝试采用的步可能失败。这意味着您提供的目标函数或非线性约束函数将返回值 Inf、NaN 或复数值。在这种情况下,算法尝试采用较小的步。
重构线性代数例程
sqp 算法使用一组不同的线性代数例程来求解二次规划子问题公式 14。这些例程在内存使用量和速度方面都比 active-set 例程更高效。
重新表示可行性例程
当不满足约束时,sqp 算法有两种新方法来求解公式 14。
fmincon 内点算法
障碍函数
使用内点法求解约束最小化问题,相当于求解一系列近似最小化问题。初始问题是
| (33) |
| (34) |
逼近问题公式 34 是一系列等式约束问题。这些问题比原来的不等式约束问题公式 33 更容易求解。
为了求解逼近问题,该算法在每次迭代中使用两种主要步之一:
默认情况下,算法首先尝试采取直接步。如果失败,它会尝试 CG 步。当逼近问题在当前迭代附近不是局部凸时,它不采取直接步。
在每次迭代中,算法都会降低评价函数的值,形式如下
| (35) |
如果目标函数或非线性约束函数在迭代 xj 中返回复数值、NaN、Inf 或错误,算法将拒绝 xj。拒绝的效果与评价函数没有充分降低时相同:然后算法尝试另一个较短的步。将可能出错的代码都包含到 try-catch 结构中:
function val = userFcn(x)
try
val = ... % code that can error
catch
val = NaN;
end目标和约束必须在初始点产生适当的 (double) 值。
直接步
直接步的定义涉及以下变量:
H 表示 fμ 的拉格朗日函数的黑塞矩阵:
(36) Jg 表示约束函数 g 的雅可比矩阵。
Jh 表示约束函数 h 的雅可比矩阵。
S = diag(s).
λ 表示与约束 g 相关联的拉格朗日乘数向量
Λ = diag(λ).
y 表示与 h 相关联的拉格朗日乘数向量。
e 表示与 g 大小相同的由 1 组成的向量。
公式 38 定义直接步 (Δx, Δs):
| (37) |
此方程直接来自尝试用线性化拉格朗日函数求解公式 2 和公式 3。
通过将第二个变量 Δs 前乘 S–1,可以使方程对称:
| (38) |
为了针对 (Δx, Δs) 求解此方程,算法对矩阵进行 LDL 分解;请参阅 ldl。这是计算量最大的步骤。这种分解的一个结果是确定投影的黑塞矩阵是否为正定;如果不是,则算法使用共轭梯度步,这将在共轭梯度步中说明。
更新障碍参数
要使逼近问题公式 34 接近原始问题,障碍参数 μ 需要随着迭代次数的增加逐渐降低至 0。该算法有两个障碍参数更新选项,您可以使用 BarrierParamUpdate 选项来指定:'monotone'(默认值)和 'predictor-corrector'。
使用 'monotone' 选项时,如果逼近问题在前一次迭代中的解足够准确,参数 μ 就会降低 1/100 或 1/5。当算法只需一次或两次迭代就能达到足够的准确度时,该选项使用 1/100,否则使用 1/5。准确度可通过以下测试来衡量,即确定公式 38 右侧的所有项的大小都小于 μ:
注意
在以下任一情况下,fmincon 都会用 'monotone' 覆盖 BarrierParamUpdate 设置:
该问题没有不等式约束,包括边界约束。
SubproblemAlgorithm选项是'cg'。
用于更新障碍参数 μ 的 'predictor-corrector' 算法类似于线性规划 预测-校正 算法。
预测-校正步可以通过调整牛顿步中的线性化错误来加速现有 Fiacco-McCormick(单调)方法。预测-校正算法具有双重效果:它通常可以改进步方向,同时用中心化参数 σ 以自适应方式更新障碍参数,以鼓励沿着“中心路径”进行迭代。请参阅 Nocedal 和 Wright [31] 对线性规划的预测-校正步的讨论,了解为什么中心路径允许更大的步长,从而更快地收敛。
预测步使用线性化步长,其中 μ = 0,这意味着没有障碍函数:
将 ɑs 和 ɑλ 定义为不违反非负性约束的最大步长。
现在根据预测步计算互补性。
| (39) |
其中 m 是约束的数量。
第一个校正步针对牛顿求根线性化中忽略的二次项进行调整
为了校正二次误差,求解线性系统以确定校正步方向。
第二个校正步是中心化步。中心化校正基于方程右侧的变量 σ
此处,σ 定义如下
其中 μP 在方程 公式 39 中定义且 。
为了防止障碍参数下降过快,从而可能导致算法不稳定,算法使中心化参数 σ 保持在 1/100 以上。此操作使障碍参数 μ 按不超过因子 1/100 的幅度降低。
在算法上,第一个校正步和中心化步是相互独立的,因此它们是一起计算的。此外,预测变量和两个校正步的左侧矩阵是相同的。因此,在算法上,该矩阵只分解一次,此分解用于所有这些步。
当建议的预测-校正步使评价函数值公式 35增大、互补性至少增大一倍或计算的惯量不正确(问题看起来是非凸的)时,该算法可以拒绝建议的预测-校正步。在这些情况下,算法尝试采取不同的步或共轭梯度步。
共轭梯度步
求解逼近问题公式 34 的共轭梯度法类似于其他共轭梯度计算。在本例中,算法会同时调整 x 和 s,从而保持松弛变量 s 为正。该方法在满足线性化约束的前提下,在信赖域中最小化逼近问题的二次逼近。
具体来说,用 R 表示信赖域的半径,并用和直接步一样的方法定义其他变量。算法近似求解以下 KKT 方程以获得拉格朗日乘数
该过程基于最小二乘法思想,且满足 λ 为正。然后,它采取步 (Δx, Δs) 以近似求解
| (40) |
| (41) |
可行性模式
当 EnableFeasibilityMode 选项为 true 并且迭代没有足够快地降低不可行性时,算法会切换到可行性模式。如果算法无法降低普通模式下的不可行性,然后在切换到共轭梯度模式后再次失败,则会发生此切换。因此,在未使用可行性模式前求解器找不到可行解的情形中,若要使这一过程最为高效,请在使用可行性模式时将 SubproblemAlgorithm 设置为 'cg'。这样做可以避免在普通模式下进行没有结果的搜索。
可行性模式算法基于 Nocedal、Öztoprak 和 Waltz [1]。该算法会忽略目标函数,改为尝试最小化不可行性,不可行性定义为不等式约束函数的正部和等式约束函数的绝对值之和。基于松弛变量 (其中各项分别对应于不等式、等式的正部和等式的负部),问题可表示为
需满足以下约束
为了求解该松弛问题,软件使用带对数障碍函数和松弛变量 的内点公式来最小化
需满足以下约束
松弛问题的求解过程从 μ 初始化为当前障碍参数值开始。松弛变量 sI 初始化为从主模式继承的当前不等式松弛值。r 变量初始化为
其余的松弛变量初始化为
从这个初始点开始,可行性模式算法重用普通内点算法的代码。此过程需要特殊的步长计算,因为 r 变量是线性的,因此其相关联的二阶导数为零。换句话说,可行性问题的目标函数黑塞矩阵秩亏。因此,该算法无法采取牛顿步。相反,该算法采用最陡下降方向步。该算法从目标关于变量的梯度开始,将梯度投影到约束的雅可比矩阵的零空间上,并重新缩放得到的向量,使其具有适当的步长。这一步可有效降低不可行性。
可行性模式算法在不可行性降低十分之一时结束。当可行性模式结束时,算法将变量 x 和 sI 传递给主算法,并丢弃其他松弛变量和松弛变量 r。
参考
[1] Nocedal, Jorge, Figen Öztoprak, and Richard A. Waltz. An Interior Point Method for Nonlinear Programming with Infeasibility Detection Capabilities. Optimization Methods & Software 29(4), July 2014, pp. 837–854.
内点算法选项
以下是内点算法中几个选项的含义和效果。
HonorBounds- 当设置为true时,每次迭代都满足您设置的边界约束。当设置为false时,算法可能会在中间迭代期间违反边界。HessianApproximation:当设置为
'bfgs'时,fmincon通过稠密矩阵拟牛顿逼近来计算黑塞矩阵。当设置为
'lbfgs'时,fmincon通过限制内存使用量的大规模拟牛顿逼近来计算黑塞矩阵。当设置为
'fin-diff-grads'时,fmincon使用梯度的有限差分计算黑塞矩阵乘以向量的结果;其他选项需要适当设置。
HessianFcn-fmincon使用您在HessianFcn中指定的函数句柄来计算黑塞矩阵。请参阅包含黑塞函数。HessianMultiplyFcn- 提供单独的函数来计算黑塞矩阵乘以向量的结果。有关详细信息,请参阅包含黑塞函数和黑塞矩阵乘法函数。SubproblemAlgorithm- 决定是否尝试直接牛顿步。默认设置'factorization'允许尝试此类型的步。设置'cg'仅允许共轭梯度步。
有关选项的完整列表,请参阅 fmincon options 中的内点算法。
fminbnd 算法
fminbnd 是任何 MATLAB® 安装中都提供的求解器。它用于求解有界区间内的一维局部最小化问题。它不基于导数。相反,它使用黄金分割搜索和抛物线插值。
fseminf 问题的表示和算法
fseminf 问题的表示
与 fmincon 求解的问题相比,fseminf 处理的优化问题还需要满足其他类型的约束。fmincon 的表示为
满足 c(x) ≤ 0, ceq(x) = 0, A·x ≤ b, Aeq·x = beq, and l ≤ x ≤ u。
fseminf 在已给出的约束基础上增加以下一组半无限约束。对于一维或二维有界区间内的 wj 或矩形 Ij,对于由连续函数 K(x, w) 组成的向量,约束为
Kj(x, wj) ≤ 0(对于所有 wj∈Ij)。
fseminf 问题的“维度”指约束集 I 的最大维度:如果所有 Ij 都是区间,则为 1;如果有至少一个 Ij 是矩形,则为 2。K 向量的大小不属于此维度概念。
之所以称之为半无限规划,原因是变量(x 和 wj)的数目有限,但约束的数目无限。这是因为对 x 的约束是在一组连续的区间或矩形 Ij 上,其中包含无限数量的点,因此存在无限数量的约束:对于无限数量的点 wj,Kj(x, wj) ≤ 0。
您可能会认为具有无限数目的约束的问题无法求解。fseminf 通过将问题重新表示为具有两个阶段(最大化和最小化)的等效问题来求解此类问题。半无限约束重新表示为
| (42) |
其中 |K| 是向量 K 的分量数目,即半无限约束函数的数目。对于固定 x,这是在有界区间或矩形上的常规最大化问题。
fseminf 通过针对求解器访问的每个 x 对函数 Kj(x, wj) 进行分段二次或三次逼近 κj(x, wj),进一步简化了问题。在公式 42 中,fseminf 仅考虑插值函数 κj(x, wj)(而不是 Kj(x, wj))的最大值。这会将原来的半无限约束函数最小化问题简化为一个约束数目有限的问题。
采样点. 您的半无限约束函数必须提供一组采样点,这些点用于进行二次或三次逼近。为此,它应包含:
采样点 w 之间的初始间距
s从
s生成一组采样点 w 的方法
初始间距 s 是一个 |K|×2 矩阵。s 的第 j 行表示约束函数 Kj 的相邻采样点的间距。如果 Kj 依赖一维 wj,请设置 s(j,2) = 0。fseminf 会在后续迭代中更新矩阵 s。
fseminf 使用矩阵 s 生成采样点 w,然后使用这些采样点创建逼近 κj(x, wj)。在优化过程中,从 s 生成 w 时,您应保持区间或矩形 Ij 不变。
创建采样点的示例. 以具有两个半无限约束 K1 和 K2 的问题为例。K1 有一维 w1,K2 有二维 w2。以下代码从 w1 = 2 到 12 生成采样集:
% Initial sampling interval
if isnan(s(1,1))
s(1,1) = .2;
s(1,2) = 0;
end
% Sampling set
w1 = 2:s(1,1):12;fseminf 在首次调用约束函数时将 s 指定为 NaN。您可以通过检查此项来设置初始采样间隔。
以下代码从 w2 生成正方形采样集,每个分量从 1 到 100,第一个分量较第二个分量有更密集的初始采样:
% Initial sampling interval if isnan(s(1,1)) s(2,1) = 0.2; s(2,2) = 0.5; end % Sampling set w2x = 1:s(2,1):100; w2y = 1:s(2,2):100; [wx,wy] = meshgrid(w2x,w2y);
前面的代码片段可以简化如下:
% Initial sampling interval
if isnan(s(1,1))
s = [0.2 0;0.2 0.5];
end
% Sampling set
w1 = 2:s(1,1):12;
w2x = 1:s(2,1):100;
w2y = 1:s(2,2):100;
[wx,wy] = meshgrid(w2x,w2y);fseminf 算法
fseminf 本质是将半无限规划问题简化为可用 fmincon 求解的问题。fseminf 采取以下步骤来求解半无限规划问题:
在 x 的当前值下,
fseminf找出所有 wj,i,使得插值 κj(x, wj,i) 是局部最大值。(对于固定的 x,最大值点是指变化的 w。)fseminf在fmincon问题的解中采取一个迭代步:使得 c(x) ≤ 0, ceq(x) = 0, A·x ≤ b, Aeq·x = beq, and l ≤ x ≤ u,其中 c(x) 使用在所有 wj∈Ij 上选取的 κj(x, wj) 的所有最大值进行了增强,这些最大值等于 κj(x, wj,i) 的 j 和 i 上的最大值。
fseminf检查新点 x 处是否满足任何停止条件(用于停止迭代);如果不满足,它继续执行步骤 4。fseminf检查半无限约束的离散化是否需要更新,并适当更新采样点。由此可得更新后的逼近 κj(x, wj)。然后继续执行步骤 1。
