lsqminnorm
线性方程的最小范数最小二乘解
语法
说明
示例
输入参数
提示
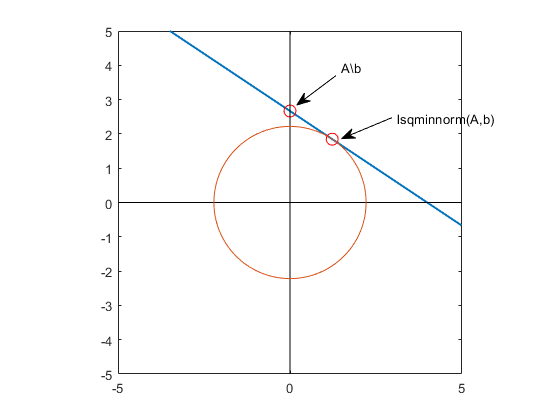
当有多个解时,
lsqminnorm计算的最小范数解具有特别的意义。只要A欠定(行数少于列数)或低秩,方程 Ax = b 就有多个解。在计算线性系统的最小范数最小二乘解时,
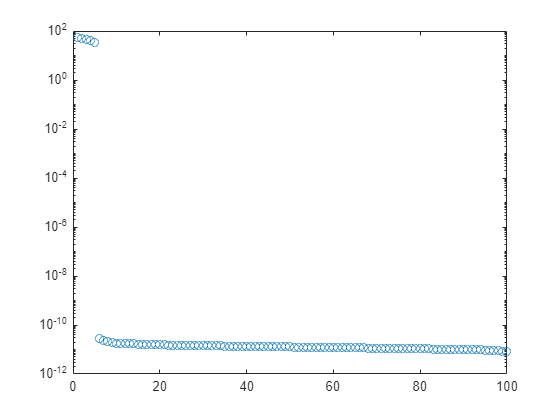
lsqminnorm(A,B,tol)的效率通常高于pinv(A,tol)*B。lsqminnorm使用完全正交分解 (COD) 来计算A的低秩逼近,而pinv使用的是奇异值分解 (SVD)。因此,pinv和lsqminnorm的结果不完全一致。对于稀疏矩阵,
lsqminnorm使用与稠密矩阵不同的算法,因此会产生不同的结果。