lsqcurvefit
用最小二乘求解非线性曲线拟合(数据拟合)问题
语法
说明
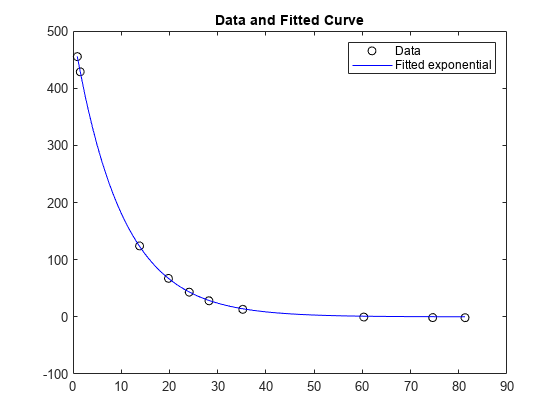
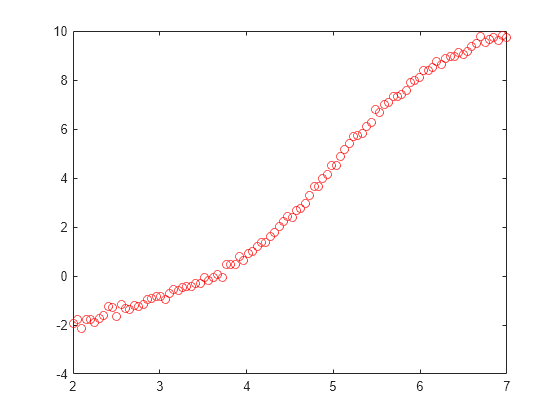
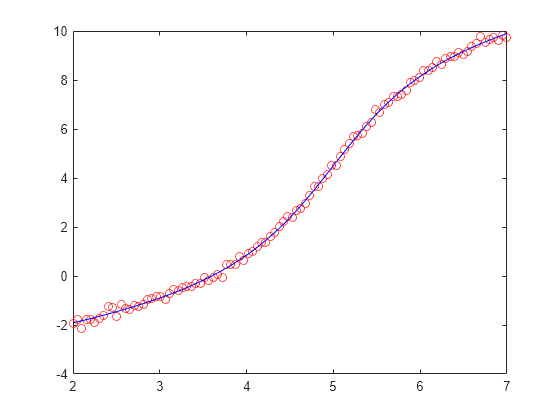
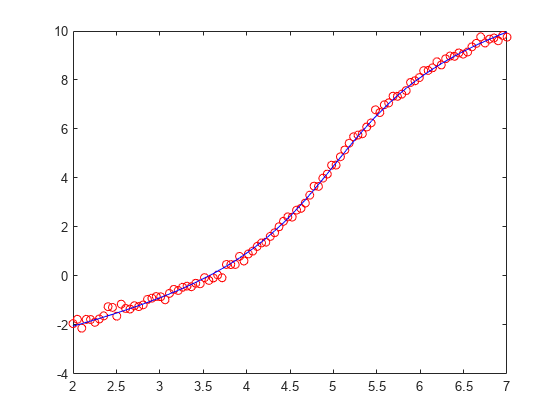
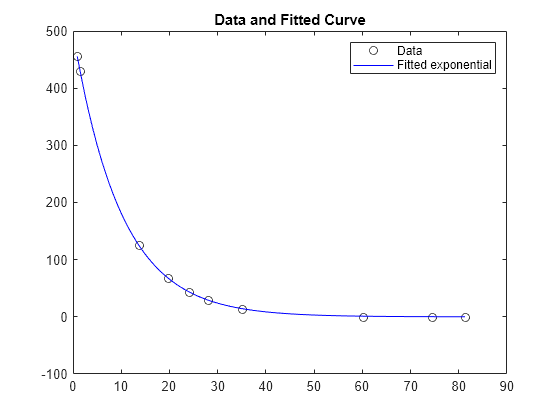
示例
输入参数
输出参量
限制
信赖域反射算法不能求解欠定方程组;它要求方程个数(即 F 的行维度)至少与变量个数一样。在欠定的情况下,
lsqcurvefit使用莱文贝格-马夸特算法。lsqcurvefit可以直接求解复数值问题。请注意,约束对于复数值没有意义,因为复数不能很好地排序;询问一个复数值是大于还是小于另一个复数值没有意义。对于具有边界约束的复数问题,请将变量分成实部和虚部。不要对复数数据使用'interior-point'算法。请参阅对复数值数据进行模型拟合。信赖域反射方法的预条件共轭梯度部分中使用的预条件子计算在计算预条件子之前形成 JTJ(其中 J 是雅可比矩阵)。因此,如果 J 的一行包含许多非零值(这会导致近乎稠密的乘积 JTJ),则可能导致大型问题的求解过程成本高昂。
如果 x 的分量没有上界(或下界),
lsqcurvefit更倾向于ub(或lb)的对应分量设置为inf(对于下界,则为-inf),而不是任意但非常大的正数(对于下界,则为负数)。
您可以在 lsqnonlin、lsqcurvefit、fsolve 中使用信赖域反射算法求解中小规模问题,而无需计算 fun 中的雅可比矩阵或提供雅可比矩阵稀疏模式。(这也适用于使用 fmincon 或 fminunc 而不计算黑塞矩阵或提供黑塞矩阵稀疏模式的情况。)中小规模有多小?没有绝对的答案,因为这取决于您的计算机系统配置中的虚拟内存量。
假设您的问题有 m 个方程和 n 个未知数。如果命令 J = sparse(ones(m,n)) 导致您的计算机上出现 Out of memory 错误,则这肯定是因为问题太大。即使它没有导致错误,问题仍可能太大。只有运行它并查看 MATLAB 是否在系统可用的虚拟内存量内运行,您才能找到答案。
详细信息
算法
莱文贝格-马夸特和信赖域反射方法基于非线性最小二乘算法,这些算法也在 fsolve 中使用。
'interior-point' 算法使用 fmincon 'interior-point' 算法,但有一些修正。有关详细信息,请参阅针对约束最小二乘修正的 fmincon 算法。
替代功能
App
优化实时编辑器任务为 lsqcurvefit 提供了一个可视化界面。
参考
[1] Coleman, T.F. and Y. Li. “An Interior, Trust Region Approach for Nonlinear Minimization Subject to Bounds.” SIAM Journal on Optimization, Vol. 6, 1996, pp. 418–445.
[2] Coleman, T.F. and Y. Li. “On the Convergence of Reflective Newton Methods for Large-Scale Nonlinear Minimization Subject to Bounds.” Mathematical Programming, Vol. 67, Number 2, 1994, pp. 189–224.
[3] Dennis, J. E. Jr. “Nonlinear Least-Squares.” State of the Art in Numerical Analysis, ed. D. Jacobs, Academic Press, pp. 269–312.
[4] Levenberg, K. “A Method for the Solution of Certain Problems in Least-Squares.” Quarterly Applied Mathematics 2, 1944, pp. 164–168.
[5] Marquardt, D. “An Algorithm for Least-squares Estimation of Nonlinear Parameters.” SIAM Journal Applied Mathematics, Vol. 11, 1963, pp. 431–441.
[6] Moré, J. J. “The Levenberg-Marquardt Algorithm: Implementation and Theory.” Numerical Analysis, ed. G. A. Watson, Lecture Notes in Mathematics 630, Springer Verlag, 1977, pp. 105–116.
[7] Moré, J. J., B. S. Garbow, and K. E. Hillstrom. User Guide for MINPACK 1. Argonne National Laboratory, Rept. ANL–80–74, 1980.
[8] Powell, M. J. D. “A Fortran Subroutine for Solving Systems of Nonlinear Algebraic Equations.” Numerical Methods for Nonlinear Algebraic Equations, P. Rabinowitz, ed., Ch.7, 1970.