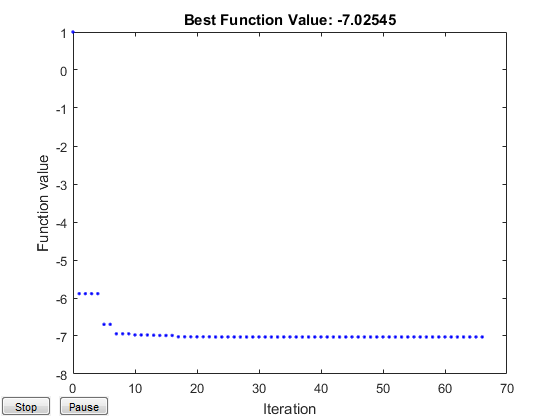
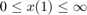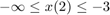patternsearch
使用模式搜索找到函数的最小值
语法
说明
示例
使用 patternsearch 求解器最小化无约束问题。
创建以下双变量目标函数。在您的 MATLAB® 路径上，将以下代码保存到名为 psobj.m 的文件中。
function y = psobj(x)
y = exp(-x(1)^2-x(2)^2)*(1+5*x(1) + 6*x(2) + 12*x(1)*cos(x(2)));
将目标函数设置为 @psobj。
fun = @psobj;
从点 [0,0] 开始，找到最小值。
x0 = [0,0]; x = patternsearch(fun,x0)
patternsearch stopped because the mesh size was less than options.MeshTolerance. x = -0.7037 -0.1860
最小化受某些线性不等式约束的函数。
创建以下双变量目标函数。在您的 MATLAB® 路径上，将以下代码保存到名为 psobj.m 的文件中。
function y = psobj(x)
y = exp(-x(1)^2-x(2)^2)*(1+5*x(1) + 6*x(2) + 12*x(1)*cos(x(2)));
将目标函数设置为 @psobj。
fun = @psobj;
设置两个线性不等式约束。
A = [-3,-2;
-4,-7];
b = [-1;-8];
从点 [0.5,-0.5] 开始，找到最小值。
x0 = [0.5,-0.5]; x = patternsearch(fun,x0,A,b)
patternsearch stopped because the mesh size was less than options.MeshTolerance.
x =
5.2827 -1.8758
找到仅具有边界的约束的最小值。
创建以下双变量目标函数。在您的 MATLAB® 路径上，将以下代码保存到名为 psobj.m 的文件中。
function y = psobj(x)
y = exp(-x(1)^2-x(2)^2)*(1+5*x(1) + 6*x(2) + 12*x(1)*cos(x(2)));
将目标函数设置为 @psobj。
fun = @psobj;
找出 
和 
时的最小值。
lb = [0,-Inf]; ub = [Inf,-3]; A = []; b = []; Aeq = []; beq = [];
从点 [1,-5] 开始，找到最小值。
x0 = [1,-5]; x = patternsearch(fun,x0,A,b,Aeq,beq,lb,ub)
patternsearch stopped because the mesh size was less than options.MeshTolerance.
x =
0.1880 -3.0000
找到受非线性不等式约束的函数的最小值。
创建以下双变量目标函数。在您的 MATLAB® 路径上，将以下代码保存到名为 psobj.m 的文件中。
function y = psobj(x)
y = exp(-x(1)^2-x(2)^2)*(1+5*x(1) + 6*x(2) + 12*x(1)*cos(x(2)));
将目标函数设置为 @psobj。
fun = @psobj;
创建非线性约束
为此，在 MATLAB 路径上，将以下代码保存到名为 ellipsetilt.m 的文件中。
function [c,ceq] = ellipsetilt(x)
ceq = [];
c = x(1)*x(2)/2 + (x(1)+2)^2 + (x(2)-2)^2/2 - 2;
从起始点 patternsearch 开始 [-2,-2]。
x0 = [-2,-2]; A = []; b = []; Aeq = []; beq = []; lb = []; ub = []; nonlcon = @ellipsetilt; x = patternsearch(fun,x0,A,b,Aeq,beq,lb,ub,nonlcon)
Optimization finished: mesh size less than options.MeshTolerance and constraint violation is less than options.ConstraintTolerance. x = -1.5144 0.0875
有时不同的 patternsearch 算法有明显不同的行为。虽然很难预测哪种算法最适合解决问题，但您可以轻松尝试不同的算法。对于此示例，使用 sawtoothxy 目标函数，该函数在运行此示例时可用，并在 寻找全局或多个局部最小值 中描述和绘制。
type sawtoothxyfunction f = sawtoothxy(x,y)
[t r] = cart2pol(x,y); % change to polar coordinates
h = cos(2*t - 1/2)/2 + cos(t) + 2;
g = (sin(r) - sin(2*r)/2 + sin(3*r)/3 - sin(4*r)/4 + 4) ...
.*r.^2./(r+1);
f = g.*h;
end
为了观察最小化该目标函数时不同算法的行为，请设置一些不对称的边界。还设置一个初始点 x0，它离真实解 sol = [0 0] 较远，其中 sawtoothxy(0,0) = 0。
rng default
x0 = 12*randn(1,2);
lb = [-15,-26];
ub = [26,15];
fun = @(x)sawtoothxy(x(1),x(2));使用 sawtoothxy "classic" 算法最小化 patternsearch 函数。
optsc = optimoptions("patternsearch",Algorithm="classic"); [sol,fval,eflag,output] = patternsearch(fun,... x0,[],[],[],[],lb,ub,[],optsc)
patternsearch stopped because the mesh size was less than options.MeshTolerance.
sol = 1×2
10-5 ×
0.9825 0
fval = 1.3278e-09
eflag = 1
output = struct with fields:
function: @(x)sawtoothxy(x(1),x(2))
problemtype: 'boundconstraints'
pollmethod: 'gpspositivebasis2n'
maxconstraint: 0
searchmethod: []
iterations: 52
funccount: 168
meshsize: 9.5367e-07
rngstate: [1×1 struct]
message: 'patternsearch stopped because the mesh size was less than options.MeshTolerance.'
"classic" 算法经过 52 次迭代和 168 次函数计算最终找到全局解。
尝试 "nups" 算法。
rng default % For reproducibility optsn = optimoptions("patternsearch",Algorithm="nups"); [sol,fval,eflag,output] = patternsearch(fun,... x0,[],[],[],[],lb,ub,[],optsn)
patternsearch stopped because the mesh size was less than options.MeshTolerance.
sol = 1×2
6.3204 15.0000
fval = 85.9256
eflag = 1
output = struct with fields:
function: @(x)sawtoothxy(x(1),x(2))
problemtype: 'boundconstraints'
pollmethod: 'nups'
maxconstraint: 0
searchmethod: []
iterations: 29
funccount: 88
meshsize: 7.1526e-07
rngstate: [1×1 struct]
message: 'patternsearch stopped because the mesh size was less than options.MeshTolerance.'
这次求解器仅仅用了 29 次迭代和 88 次函数计算就达到了局部解，但该解并不是全局解。
尝试使用 "nups-mads" 算法，该算法在坐标方向上不采取任何步骤。
rng default % For reproducibility optsm = optimoptions("patternsearch",Algorithm="nups-mads"); [sol,fval,eflag,output] = patternsearch(fun,... x0,[],[],[],[],lb,ub,[],optsm)
patternsearch stopped because the mesh size was less than options.MeshTolerance.
sol = 1×2
10-4 ×
-0.5275 0.0806
fval = 1.5477e-08
eflag = 1
output = struct with fields:
function: @(x)sawtoothxy(x(1),x(2))
problemtype: 'boundconstraints'
pollmethod: 'nups-mads'
maxconstraint: 0
searchmethod: []
iterations: 55
funccount: 189
meshsize: 9.5367e-07
rngstate: [1×1 struct]
message: 'patternsearch stopped because the mesh size was less than options.MeshTolerance.'
这次，求解器在 55 次迭代和 189 次函数计算中达到了全局解，这与 'classic' 算法类似。
设置选项以观察 patternsearch 解过程的进度。
创建以下双变量目标函数。在您的 MATLAB® 路径上，将以下代码保存到名为 psobj.m 的文件中。
function y = psobj(x)
y = exp(-x(1)^2-x(2)^2)*(1+5*x(1) + 6*x(2) + 12*x(1)*cos(x(2)));将目标函数设置为 @psobj。
fun = @psobj;
设置 options 以提供迭代显示并在每次迭代时绘制目标函数。
options = optimoptions('patternsearch','Display','iter','PlotFcn',@psplotbestf);
从点 [0,0] 开始找到目标的无约束最小值。
x0 = [0,0]; A = []; b = []; Aeq = []; beq = []; lb = []; ub = []; nonlcon = []; x = patternsearch(fun,x0,A,b,Aeq,beq,lb,ub,nonlcon,options)
Iter f-count f(x) MeshSize Method
0 1 1 1
1 4 -5.88607 2 Successful Poll
2 8 -5.88607 1 Refine Mesh
3 12 -5.88607 0.5 Refine Mesh
4 16 -5.88607 0.25 Refine Mesh
(output trimmed)
63 218 -7.02545 1.907e-06 Refine Mesh
64 221 -7.02545 3.815e-06 Successful Poll
65 225 -7.02545 1.907e-06 Refine Mesh
66 229 -7.02545 9.537e-07 Refine Mesh
Optimization terminated: mesh size less than options.MeshTolerance.
x =
-0.7037 -0.1860找到函数的最小值并报告最小值的位置和值。
创建以下双变量目标函数。在您的 MATLAB® 路径上，将以下代码保存到名为 psobj.m 的文件中。
function y = psobj(x)
y = exp(-x(1)^2-x(2)^2)*(1+5*x(1) + 6*x(2) + 12*x(1)*cos(x(2)));
将目标函数设置为 @psobj。
fun = @psobj;
从点 [0,0] 开始，找到目标的无约束最小值。返回最小值 x 的位置和 fun(x) 的值。
x0 = [0,0]; [x,fval] = patternsearch(fun,x0)
patternsearch stopped because the mesh size was less than options.MeshTolerance. x = -0.7037 -0.1860 fval = -7.0254
为了检查 patternsearch 解过程，获取所有输出。
创建以下双变量目标函数。在您的 MATLAB® 路径上，将以下代码保存到名为 psobj.m 的文件中。
function y = psobj(x)
y = exp(-x(1)^2-x(2)^2)*(1+5*x(1) + 6*x(2) + 12*x(1)*cos(x(2)));
将目标函数设置为 @psobj。
fun = @psobj;
从点 [0,0] 开始，找到目标的无约束最小值。返回解、x、解处的目标函数值、fun(x)、退出标志和输出结构体。
x0 = [0,0]; [x,fval,exitflag,output] = patternsearch(fun,x0)
patternsearch stopped because the mesh size was less than options.MeshTolerance.
x =
-0.7037 -0.1860
fval =
-7.0254
exitflag =
1
output =
struct with fields:
function: @psobj
problemtype: 'unconstrained'
pollmethod: 'gpspositivebasis2n'
maxconstraint: []
searchmethod: []
iterations: 66
funccount: 229
meshsize: 9.5367e-07
rngstate: [1×1 struct]
message: 'patternsearch stopped because the mesh size was less than options.MeshTolerance.'
exitflag 是 1，表示收敛到局部最小值。
output 结构体包含 patternsearch 进行了多少次迭代以及进行了多少次函数计算等信息。将此输出结构与 使用非默认选项的模式搜索 的结果进行比较。在该示例中，您获得了部分信息，但并未获得诸如函数计算的次数之类的信息。
输入参数
输出参量
算法
默认情况下，在没有线性约束的情况下，patternsearch 会根据与坐标方向一致的自适应网格寻找最小值。请参阅什么是直接搜索？和模式搜索轮询的工作原理。
当您将 Algorithm 选项设置为 "nups" 或其变体之一时，patternsearch 将使用 非均匀模式搜索 (NUPS) 算法 中描述的算法。该算法与默认算法有几个不同之处；例如，它需要设置的选项更少。
替代功能
App
优化实时编辑器任务为 patternsearch 提供了一个可视化界面。
参考
[1] Audet, Charles, and J. E. Dennis Jr. “Analysis of Generalized Pattern Searches.” SIAM Journal on Optimization. Volume 13, Number 3, 2003, pp. 889–903.
[2] Conn, A. R., N. I. M. Gould, and Ph. L. Toint. “A Globally Convergent Augmented Lagrangian Barrier Algorithm for Optimization with General Inequality Constraints and Simple Bounds.” Mathematics of Computation. Volume 66, Number 217, 1997, pp. 261–288.
[3] Abramson, Mark A. Pattern Search Filter Algorithms for Mixed Variable General Constrained Optimization Problems. Ph.D. Thesis, Department of Computational and Applied Mathematics, Rice University, August 2002.
[4] Abramson, Mark A., Charles Audet, J. E. Dennis, Jr., and Sebastien Le Digabel. “ORTHOMADS: A deterministic MADS instance with orthogonal directions.” SIAM Journal on Optimization. Volume 20, Number 2, 2009, pp. 948–966.
[5] Kolda, Tamara G., Robert Michael Lewis, and Virginia Torczon. “Optimization by direct search: new perspectives on some classical and modern methods.” SIAM Review. Volume 45, Issue 3, 2003, pp. 385–482.
[6] Kolda, Tamara G., Robert Michael Lewis, and Virginia Torczon. “A generating set direct search augmented Lagrangian algorithm for optimization with a combination of general and linear constraints.” Technical Report SAND2006-5315, Sandia National Laboratories, August 2006.
[7] Lewis, Robert Michael, Anne Shepherd, and Virginia Torczon. “Implementing generating set search methods for linearly constrained minimization.” SIAM Journal on Scientific Computing. Volume 29, Issue 6, 2007, pp. 2507–2530.
扩展功能
版本历史记录
在 R2006a 之前推出
