探索 `patternsearch` 算法

从 R2022b 开始，patternsearch 有四种算法：

"classic"
"nups"（非均匀模式搜索）
"nups-gps"
"nups-mads"

这个例子说明了算法的选择如何影响具有非光滑目标函数的有界问题。

目标函数

此示例的目标函数基于运行示例时可用的 2-D ps_example 函数。

type ps_example

function f = ps_example(x)
%PS_EXAMPLE objective function for patternsearch.

%   Copyright 2003-2021 The MathWorks, Inc.

f = zeros(1,size(x,1));
for i = 1:size(x,1)
    if  x(i,1) < -5
        f(i) = (x(i,1)+5)^2 + abs(x(i,2));
    elseif x(i,1) < -3
        f(i) = -2*sin(x(i,1)) + abs(x(i,2));
    elseif x(i,1) < 0
        f(i) = 0.5*x(i,1) + 2 + abs(x(i,2));
    elseif x(i,1) >= 0
        f(i) = .3*sqrt(x(i,1)) + 5/2 +abs(x(i,2));
    end
end

通过为每两个维度创建距离原点的伪随机偏移，并添加得到的目标，将 ps_example 函数扩展到任意偶数维。请参阅本示例末尾的 testps 辅助函数的代码。

指定 N = 10 尺寸，并为每个分量设置 -20 到 20 的边界。从点 x0 = [0 0 ... 0] 开始 patternsearch。

N = 10;
lb = -20*ones(1,N);
ub = -lb;
x0 = zeros(size(lb));

运行经典算法

设置选项以使用 "classic" 算法并显示目标函数值。

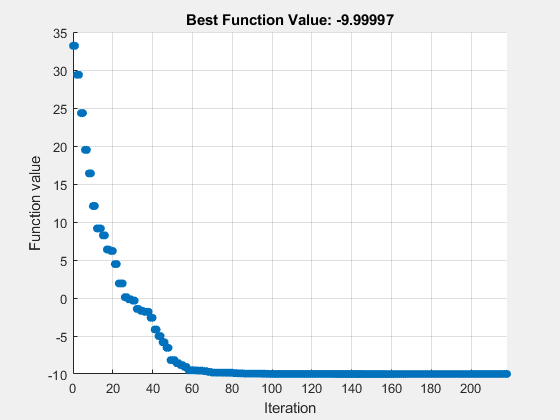
optscl = optimoptions("patternsearch",Algorithm="classic",PlotFcn="psplotbestf");

运行优化。

[xclassic,fvalclassic,eflagclassic,outputclassic] = ...
    patternsearch(@testps,x0,[],[],[],[],lb,ub,[],optscl)

patternsearch stopped because the mesh size was less than options.MeshTolerance.

xclassic = 1×10

   -7.9575    5.9058   -8.5047   -5.5481   -8.9402   -2.8633   -7.5058    0.8919   -5.6967    2.9322

fvalclassic = -10.0000

eflagclassic = 1

outputclassic = struct with fields:
         function: @testps
      problemtype: 'boundconstraints'
       pollmethod: 'gpspositivebasis2n'
    maxconstraint: 0
     searchmethod: []
       iterations: 218
        funccount: 3487
         meshsize: 9.5367e-07
         rngstate: [1x1 struct]
          message: 'patternsearch stopped because the mesh size was less than options.MeshTolerance.'

运行 NUPS 算法

设置选项以使用 "nups" 算法。为了获得可重复的结果，请设置随机种子。

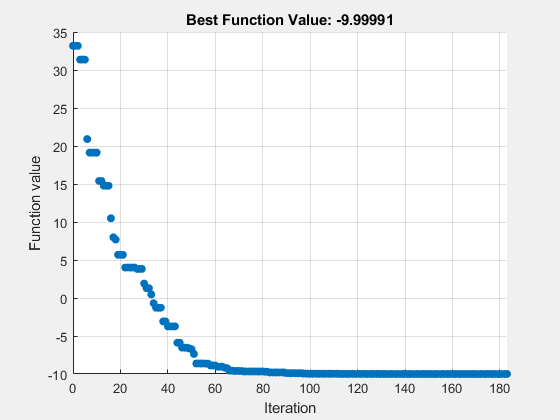
optsnups = optimoptions(optscl,Algorithm="nups");
rng default % For reproducibility
[xnups,fvalnups,eflagnups,outputnups] = ...
    patternsearch(@testps,x0,[],[],[],[],lb,ub,[],optsnups)

patternsearch stopped because the mesh size was less than options.MeshTolerance.

xnups = 1×10

   -7.9575    5.9058   -8.5047   -5.5480   -8.9401   -2.8633   -7.5058    0.8919   -5.6967    2.9322

fvalnups = -9.9999

eflagnups = 1

outputnups = struct with fields:
         function: @testps
      problemtype: 'boundconstraints'
       pollmethod: 'nups'
    maxconstraint: 0
     searchmethod: []
       iterations: 183
        funccount: 1827
         meshsize: 8.5928e-07
         rngstate: [1x1 struct]
          message: 'patternsearch stopped because the mesh size was less than options.MeshTolerance.'

在这种情况下，"nups" 算法使用更少的函数计算，但本质上达到了与 "classic" 算法相同的解。

进一步探索

您还可以尝试 "nups-gps" 和 "nups-mads" 算法来查看它们解决这个问题的表现。尽管您无法总是预测哪种算法最适合解决问题，但 "nups" 可以成为一个很好的起始算法，因为它结合了许多自适应特性，使其很可能成为最佳算法。

辅助函数

以下代码会创建 testps 辅助函数。

function y = testps(x) 
    N = numel(x); % Number of variables
    if mod(N,2) == 1
        disp("Number of variables must be even.")
        return
    end
    strm = RandStream("twister",Seed=1); % Set Seed for consistency
    % Use RandStream to avoid affecting the global stream
    dsp = 5*randn(strm,size(x));
    z = x - dsp; % Include random offsets
    y = 0;
    for i = 1:N/2
        y = y + ps_example(z([2*i-1,2*i]));
    end
end

另请参阅

patternsearch

探索 patternsearch 算法