模式搜索轮询的工作原理

本页采用了机器翻译。点击此处可查看最新英文版本。

模式搜索轮询的工作原理

上下文

patternsearch 找到接近最优点的一系列点，x0、x1、x2、...。目标函数的值从序列中的每个点到下一个点要么减小，要么保持不变。本节说明使用 GPS 算法进行优化中描述的函数的模式搜索工作原理。

为了简化解释，本节描述了广义模式搜索 (GPS) 如何使用默认最大正基 2 N 并将 ScaleMesh 选项设置为 false 来工作。

本节未显示 patternsearch 算法如何与边界或线性约束一起工作。对于边界和线性约束，patternsearch 修改轮询点以使其在每次迭代中都可行，即满足所有边界和线性约束。

本节不包含非线性约束。要了解 patternsearch 如何与非线性约束一起工作，请参阅用于模式搜索的非线性约束求解算法。

成功的轮询

模式搜索从您提供的初始点 x0 开始。在此示例中为 x0 = [2.1 1.7]。

迭代 1

在第一次迭代中，网格大小为 1，GPS 算法将模式向量添加到初始点 x0 = [2.1 1.7] 以计算以下网格点：

[1 0] + x0 = [3.1 1.7]
[0 1] + x0 = [2.1 2.7]
[-1 0] + x0 = [1.1 1.7]
[0 -1] + x0 = [2.1 0.7]

该算法按照上面显示的顺序计算网格点处的目标函数。下图显示了初始点和网格点处的目标函数值。

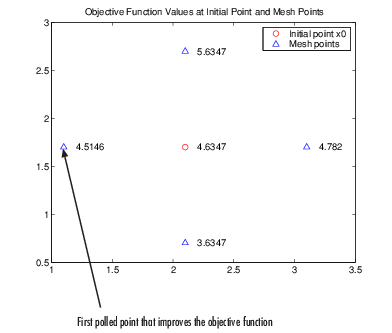
该算法通过计算目标函数值轮询网格点，直到找到一个值小于 x0 处的值 4.6347 的网格点。在这种情况下，它找到的第一个这样的点是 [1.1 1.7]，此时目标函数的值为 4.5146，因此第 1 次迭代的轮询成功。该算法将序列中的下一个点设置为

x1 = [1.1 1.7]

注意

默认情况下，GPS 模式搜索算法一旦找到适应度值小于当前点的网格点，就会停止当前迭代。因此，该算法可能不会轮询所有网格点。您可以通过将 UseCompletePoll 选项设置为 true 来让算法轮询所有网格点。

迭代 2

轮询成功后，算法将当前网格大小乘以 2，即 MeshExpansionFactor 选项的默认值。因为初始网格大小为 1，所以第二次迭代时网格大小为 2。第 2 次迭代的网格包含以下点：

2*[1 0] + x1 = [3.1 1.7]
2*[0 1] + x1 = [1.1 3.7]
2*[-1 0] + x1 = [-0.9 1.7]
2*[0 -1] + x1 = [1.1 -0.3]

下图显示了点 x1 和网格点，以及目标函数的对应值。

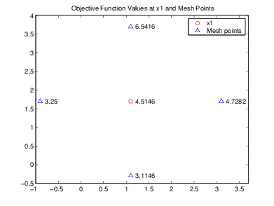
该算法轮询网格点，直到找到一个值小于 x1 处的值 4.5146 的网格点。它找到的第一个这样的点是 [-0.9 1.7]，此时目标函数的值为 3.25，因此第 2 次迭代的轮询再次成功。该算法将序列中的第二个点设置为

x2 = [-0.9 1.7]

由于轮询成功，算法将当前网格大小乘以 2，在第三次迭代时得到网格大小 4。

失败的轮询

到第四次迭代时，当前点为

x3 = [-4.9 1.7]

网格大小为 8，因此网格由以下点组成

8*[1 0] + x3 = [3.1 1.7]
8*[0 1] + x3 = [-4.9 9.7]
8*[-1 0] + x3 = [-12.9 1.7]
8*[0 -1] + x3 = [-4.9 -1.3]

下图显示了网格点及其目标函数值。

在这次迭代中，没有任何一个网格点的目标函数值小于 x3 处的值，因此轮询不成功。在这种情况下，算法在下一次迭代时不会改变当前点。即：

x4 = x3;

在下一次迭代中，算法将当前网格大小乘以 0.5（MeshContractionFactor 选项的默认值），以便下一次迭代的网格大小为 4。然后，该算法以较小的网格大小轮询。

MADS 中成功和失败的轮询

将 PollMethod 选项设置为 'MADSPositiveBasis2N' 或 'MADSPositiveBasisNp1' 会导致 patternsearch 使用不同的轮询类型，并对轮询做出与其他轮询算法不同的反应。

MADS 轮询在每次迭代时使用新生成的伪随机网格向量。这些向量是随机下三角矩阵的列中随机打乱的分量。矩阵的分量具有最大为 1/ $\sqrt{mesh size}$ 的整数大小。在轮询中，网格向量乘以网格大小，因此轮询点可以从当前点最多到达 $\sqrt{mesh size}$ 。

不成功的轮询会使网格收缩 4 倍，忽略 MeshContractionFactor 选项。类似地，成功的轮询会将网格扩大 4 倍，而忽略 MeshExpansionFactor 选项。不管 1 选项如何设置，最大网格大小都是 MaxMeshSize。

另外，当有一次轮询成功时，patternsearch 会从成功点开始再次轮询。这个额外的轮询使用相同的网格向量，扩大了 4 倍，同时保持低于 1 大小。额外的轮询再次沿着刚刚成功的相同方向进行。

显示每次迭代的结果

您可以通过将 Display 选项设置为 'iter' 来显示每次迭代的模式搜索的结果。这使您能够评估模式搜索的进度并在必要时对 options 进行更改。

通过此设置，模式搜索会在命令行上显示有关每次迭代的信息。前四次迭代是

Iter     f-count          f(x)      MeshSize     Method
    0        1        4.63474             1      
    1        4        4.51464             2     Successful Poll
    2        7           3.25             4     Successful Poll
    3       10      -0.264905             8     Successful Poll
    4       14      -0.264905             4     Refine Mesh

Successful Poll 下面的条目 Method 表示当前迭代成功。例如，第 2 次迭代的轮询成功。结果，第 2 次迭代计算出的点的目标函数值（显示在 f(x) 下方）小于第 1 次迭代的值。

在第 4 次迭代中，条目 Refine Mesh 告诉您轮询不成功。因此，第 4 次迭代中的函数值与第 3 次迭代相比保持不变。

默认情况下，模式搜索在每次成功轮询后将网格大小加倍，在每次不成功轮询后将其减半。

轮询方法

在每次迭代中，模式搜索轮询当前网格中的点 - 也就是说，它计算网格点处的目标函数，以查看是否存在一个函数值小于当前点处的函数值。模式搜索轮询的工作原理提供了轮询的一个例子。您可以通过 PollMethod 选项指定定义网格的模式。默认模式 'GPSPositiveBasis2N' 由以下 2 个 N 方向组成，其中 N 是目标函数的独立变量的数量。

[1 0 0...0]
[0 1 0...0]
...
[0 0 0...1]
[–1 0 0...0]
[0 –1 0...0]
[0 0 0...–1]。

例如，如果目标函数有三个独立变量，则 GPS Positive basis 2N 由以下六个向量组成。

[1 0 0]
[0 1 0]
[0 0 1]
[–1 0 0]
[0 –1 0]
[0 0 –1]。

或者，您可以将 PollMethod 选项设置为 'GPSPositiveBasisNp1'，即由以下 N + 1 个方向组成的模式。

[1 0 0...0]
[0 1 0...0]
...
[0 0 0...1]
[–1 –1 –1...–1]。

例如，如果目标函数有三个独立变量，则 'GPSPositiveBasisNp1' 由以下四个向量组成。

[1 0 0]
[0 1 0]
[0 0 1]
[–1 –1 –1].

使用 'GPSPositiveBasisNp1' 而不是 'GPSPositiveBasis2N' 作为 PollMethod 模式搜索有时会运行得更快，因为该算法在每次迭代中搜索的点更少。虽然此例中没有提到，但在使用 'MADSPositiveBasisNp1' 而不是 'MADSPositiveBasis2N' 时也是如此，对于 GSS 来说也是如此。例如，如果对使用 patternsearch 和 Optimize 实时编辑器任务进行约束最小化中的线性约束示例运行模式搜索，则算法使用 'GPSPositiveBasis2N'、默认的 PollMethod 执行 1588 次函数计算，但使用 'GPSPositiveBasisNp1' 仅执行 877 次函数计算。如需了解更多详细信息，请参阅使用 patternsearch 搜索全局最小值。

但是，如果目标函数有许多局部极小值，则使用 'GPSPositiveBasis2N' 作为 PollMethod 可能会避免找到非全局最小值的局部最小值，因为搜索在每次迭代中都会探索当前点周围的更多点。

完全轮询

默认情况下，如果模式搜索找到可以改善目标函数值的网格点，它将停止轮询并将该点设置为下一次迭代的当前点。当发生这种情况时，某些网格点可能无法被轮询。其中一些未轮询点的目标函数值可能比模式搜索找到的第一个点的目标函数值还要低。

对于存在多个局部极小值的问题，有时最好在每次迭代时使模式搜索轮询所有网格点，并选择具有最佳目标函数值的网格点。这使得模式搜索能够在每次迭代中探索更多的点，从而可能避免非全局最小值的局部最小值。让模式搜索轮询整个网格，将 UseCompletePoll 选项设置为 true。

模式搜索的停止条件

当下列任一情况发生时，算法停止：

网格大小小于 MeshTolerance 选项。
算法执行的迭代次数达到 MaxIterations 选项的值。
算法执行的目标函数评估总次数达到 MaxFunctionEvaluations 选项的值。
算法运行的时间（以秒为单位），直到达到 MaxTime 选项的值。
轮询成功后，前两次迭代找到的点与网格大小之间的距离都小于 StepTolerance 选项。
轮询成功后，前两次迭代中目标函数的变化小于 FunctionTolerance 选项，并且网格大小小于 StepTolerance 选项。

ConstraintTolerance 选项不用作停止条件。它确定了非线性约束的可行性。

MADS 算法在网格大小停止条件中使用了一个称为轮询参数 Δ _p 的附加参数：

$Δ_{p} = {\begin{array}{l} N \sqrt{Δ_{m}} & for positive basis N + 1 poll \\ \sqrt{Δ_{m}} & for positive basis 2 N poll, \end{array}$

其中 Δ _m 是网格大小。MADS 停止条件是：

Δ _p ≤ MeshTolerance。

模式搜索的稳健性

模式搜索算法对于目标函数失败具有很强的鲁棒性。这意味着 patternsearch 可以容忍函数计算产生 NaN、Inf 或复数值。当初始点 x0 处的目标函数是实数有限值时，patternsearch 会将轮询点失败视为目标函数值很大，并将其忽略。

例如，如果轮询中的所有点的评估结果均为 NaN，则 patternsearch 认为轮询不成功，缩小网格，然后重新评估。如果轮询中哪怕有一个点的评估值比迄今为止看到的任何值都小，patternsearch 就会认为轮询成功，并扩大网格。