使用 patternsearch 和 Optimize 实时编辑器任务进行约束最小化

使用 `patternsearch` 和 `Optimize` 实时编辑器任务进行约束最小化

此示例展示了如何使用优化实时编辑器任务（提供可视化方法）和命令行来解决约束最小化问题。

问题描述

该问题涉及在使用 patternsearch 最小化非线性函数时使用线性和非线性约束。目标函数为

$F (x) = \frac{1}{2} x^{T} H x + f^{T} x,$

其中

H = [36 17 19 12  8 15; 
     17 33 18 11  7 14; 
     19 18 43 13  8 16;
     12 11 13 18  6 11; 
      8  7  8  6  9  8; 
     15 14 16 11  8 29];

f = [ 20 15 21 18 29 24 ]';
 
F = @(x)0.5*x'*H*x + f'*x;

线性约束是

$\begin{matrix} A \cdot x \leq b, \\ A e q \cdot x = b e q, \end{matrix}$

其中

A = [-8 7 3 -4 9 0];
b = 7;
Aeq = [7 1 8 3 3 3;
      5 0 -5 1 -5 8;
     -2 -6 7 1 1 9;
      1 -1 2 -2 3 -3];
beq = [84 62 65 1]';

在继续之前，输入前面的代码部分以将问题变量放入您的工作区。

在优化实时编辑器任务中使用 `patternsearch` 进行求解

点击主页选项卡上文件部分中的新建实时脚本按钮，创建一个新的实时脚本。
插入一个优化实时编辑器任务。点击插入选项卡，然后在代码部分中选择任务 > 优化。
对于此示例，请选择基于求解器的任务。
指定问题类型
在任务的指定问题类型部分，点击目标 > 非线性按钮。
点击约束> 线性不等式和线性等式按钮。
选择求解器 > patternsearch - 模式搜索。
选择问题数据
在任务的选择问题数据部分输入问题变量。要指定目标函数，请选择目标函数> 函数句柄并选择 F。
将不等式约束设置为 A 和 b。将等式约束设置为 Aeq 和 beq。
要设置初始点，首先需要在任务上方创建一个新的部分。为此，点击插入选项卡上的分节符按钮。在任务上方的新节中，输入以下初始点代码。
```
x0 = [2 1 0 9 1 0]';
```
运行该部分将 x0 放入工作区。要运行该部分，请将光标放在该部分并按 Ctrl+Enter 或点击行号左侧的蓝色条纹。
在任务的选择问题数据部分，将 x0 设置为初始点。
指定求解器选项
由于该问题是线性约束的，因此请指定一个附加求解器选项。展开任务的指定求解器选项部分，然后点击添加按钮。将轮询设置 >轮询方法设置为 GSSPositiveBasis2N。有关 GSS 轮询方法针对线性约束问题的效率的更多信息，请参阅使用 patternsearch 搜索全局最小值。
设置显示选项
在任务的显示进度部分，选择最佳值和网格大小绘图函数。
您的设置如下所示：
运行求解器并检查结果
要运行求解器，请点击任务窗口右上角的选项按钮 ⁝，并选择运行节。
图表出现在单独的图形窗口和任务输出区域中。
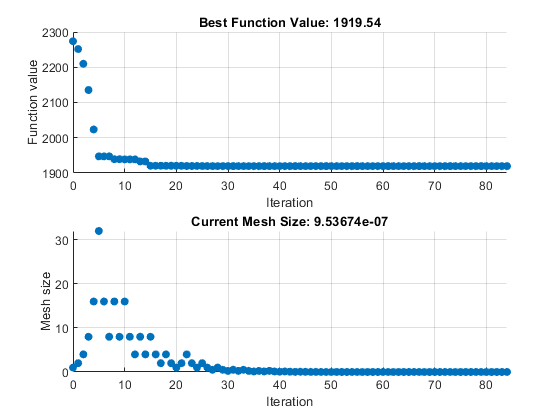
要获取解点和解处的目标函数值，请查看任务的顶部。
Optimize 实时编辑器任务在名为 solution 的变量中返回解，并在名为 objectiveValue 的变量中返回目标函数值。通过在任务下方的部分中输入以下代码然后运行该部分，或者在 MATLAB^® 命令行中输入代码来查看这些值。
```
disp(solution)
```
```
    8.5165
   -6.1094
    4.0989
    1.2877
   -4.2348
    2.1812
```
```
disp(objectiveValue)
```
```
   1.9195e+03
```
包括非线性约束
向问题添加以下非线性约束。
$\begin{matrix} - 1.5 + x_{1} x_{2} + x_{1} - x_{2} \leq 0 \\ - x_{1} x_{2} - 10 \leq 0. \end{matrix}$
要包含这些约束，首先点击约束 > 非线性按钮。
在选择问题数据部分的约束下，选择非线性 > 局部函数，然后点击新建按钮。该函数出现在任务下方的新节中。编辑生成的代码以包含以下行。
```
function [c, ceq] = double_ineq(x)
c = [-1.5 + x(1)*x(2) + x(1) - x(2);
    -x(1)*x(2) - 10];
ceq = [];
end
```
在非线性约束部分，选择 double_ineq。
非线性约束算法导致 patternsearch 需要进行多次函数计算。在指定求解器选项部分中，点击当前选项右侧的加号以显示其他选项。然后将最大函数评估限制增加到 5e4。
再次运行任务以重新运行优化。

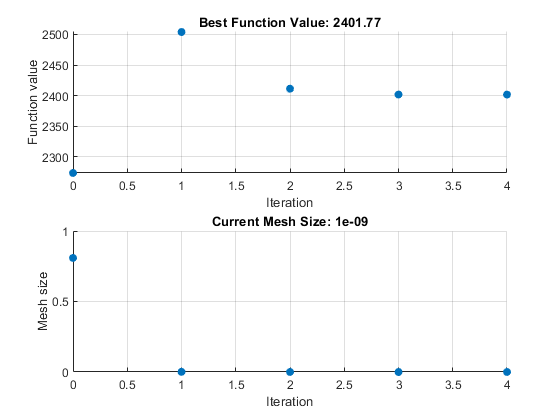
查看解和目标函数值。

disp(solution)

disp(objectiveValue)

   2.4018e+03

目标函数值高于没有非线性约束的问题中的值。先前的解对于非线性约束来说是可行的。

图表显示的迭代次数比以前少很多，因为非线性约束算法改变了 patternsearch 算法，包含另一个外循环来解决修改后的问题。外循环减少了每次主要迭代时对问题的修改。在这种情况下，该算法仅进行四次外迭代。有关算法的详细信息，请参阅用于模式搜索的非线性约束求解算法。

在命令行中使用 `patternsearch` 求解

要在命令行解决原始问题（仅线性约束），请执行以下代码。

x0 = [2 1 0 9 1 0]';
options = optimoptions('patternsearch',...
    'PollMethod','GSSPositiveBasis2N',...
    'PlotFcn',{'psplotbestf','psplotmeshsize'});
lb = [];
ub = [];
nonlcon = [];
[x,fval] = patternsearch(F,x0,A,b,Aeq,beq,lb,ub,nonlcon,options)

Optimization terminated: mesh size less than options.MeshTolerance.

x =

    8.5165
   -6.1094
    4.0989
    1.2877
   -4.2348
    2.1812


fval =

   1.9195e+03

patternsearch 生成优化实时编辑器任务示例中显示的第一对图。

要包含非线性约束，请将以下代码保存到 MATLAB 路径上名为 double_ineq.m 的文件中。

function [c, ceq] = double_ineq(x)
c = [-1.5 + x(1)*x(2) + x(1) - x(2);
    -x(1)*x(2) - 10];
ceq = [];
end

为了使求解器能够在非线性约束下完成运行，请增加允许的函数计算次数。

options.MaxFunctionEvaluations = 5e4;

解决包括非线性约束的问题。

nonlcon = @double_ineq;
[x,fval] = patternsearch(F,x0,A,b,Aeq,beq,lb,ub,nonlcon,options)

Optimization terminated: mesh size less than options.MeshTolerance
 and constraint violation is less than options.ConstraintTolerance.

x =

    7.2083
   -1.3873
    4.9579
   -3.1393
   -3.1843
    4.7457


fval =

   2.4018e+03

patternsearch 还生成了优化实时编辑器任务示例中所示的第二对图。

优化实时编辑器任务和命令行均允许您制定和解决问题，并且它们会给出相同的结果。命令行更加精简，但对于选择求解器、设置问题以及选择绘图函数等选项提供的帮助较少。您还可以使用优化启动问题，然后生成用于命令行的代码，如使用优化实时编辑器任务或求解器的有约束非线性问题所示。

另请参阅

patternsearch