本页采用了机器翻译。点击此处可查看最新英文版本。

并行优化 ODE

此示例说明如何优化 ODE 的参数。

它还展示了当 ODE 解返回目标和非线性约束函数时如何避免计算两次。该示例从运行求解器的时间和解的质量方面对 patternsearch 和 ga 进行了比较。

您需要 Parallel Computing Toolbox™ 许可证才能使用并行计算。

步骤 1.定义问题。

问题是改变大炮的位置和角度，以便将炮弹发射到尽可能远的墙壁之外。该炮的炮口速度为 300 米/秒。墙高 20 米。如果大炮离墙壁太近，它就必须以太陡的角度射击，而射弹的飞行距离就不够远。如果大炮离墙壁太远，射弹也不会飞得足够远。

空气阻力使射弹的速度减慢。阻力与速度的平方成正比，比例常数为 0.02。重力作用于抛射物，使其以恒定的 9.81 m/s2 的速度向下加速。因此，轨迹 x(t) 的运动方程为

d2x(t)dt2=−0.02‖v(t)‖v(t)−(0,9.81),

其中 v(t)​=dx(t)/dt.

初始位置 x0 和初始速度 xp0 是二维向量。但是初始高度 x0(2) 为 0，所以初始位置仅取决于标量 x0(1)。并且初始速度 xp0 的大小为 300（枪口速度），因此仅取决于初始角度，一个标量。对于初始角度 th, xp0 = 300*(cos(th),sin(th))。因此，优化问题仅取决于两个标量，所以它是一个二维问题。使用水平距离和角度作为决策变量。

步骤 2.构建 ODE 模型。

ODE 求解器要求您将模型制定为一阶系统。将轨迹向量(x1(t),x2(t)) 与其时间导数 (x'1(t),x'2(t)) 进行增强，以形成 4-D 轨迹向量。就这个增广向量而言，微分方程变成

ddtx(t)=[x3(t)x4(t)−.02‖(x3(t),x4(t))‖x3(t)−.02‖(x3(t),x4(t))‖x4(t)−9.81].

将微分方程写成函数文件，并将其保存在 MATLAB® 路径下。

function f = cannonfodder(t,x)

f = [x(3);x(4);x(3);x(4)]; % Initial, gets f(1) and f(2) correct
nrm = norm(x(3:4)) * .02; % Norm of the velocity times constant
f(3) = -x(3)*nrm; % Horizontal acceleration
f(4) = -x(4)*nrm - 9.81; % Vertical acceleration

以 pi/3 的角度从距离墙壁 30 米处开始可视化 ODE 的解。

 用于生成图窗的代码

步骤 3.使用模式搜索解决。

问题是找到初始位置 x0(1) 和初始角度 x0(2)，以最大化射弹与墙壁的距离。因为这是一个最大化问题，所以最小化距离的负数（请参阅最大化与最小化）。

要使用 patternsearch 来解决这个问题，您必须提供目标、约束、初始猜测和选项。

这两个文件是目标函数和约束函数。将它们复制到 MATLAB 路径上的文件夹中。

function f = cannonobjective(x)
x0 = [x(1);0;300*cos(x(2));300*sin(x(2))];

sol = ode45(@cannonfodder,[0,15],x0);

% Find the time t when y_2(t) = 0
zerofnd = fzero(@(r)deval(sol,r,2),[sol.x(2),sol.x(end)]);
% Then find the x-position at that time
f = deval(sol,zerofnd,1);

f = -f; % take negative of distance for maximization



function [c,ceq] = cannonconstraint(x)

ceq = [];
x0 = [x(1);0;300*cos(x(2));300*sin(x(2))];

sol = ode45(@cannonfodder,[0,15],x0);

if sol.y(1,end) <= 0 % Projectile never reaches wall
    c = 20 - sol.y(2,end);
else
    % Find when the projectile crosses x = 0
    zerofnd = fzero(@(r)deval(sol,r,1),[sol.x(2),sol.x(end)]);
    % Then find the height there, and subtract from 20
    c = 20 - deval(sol,zerofnd,2);
end

请注意，目标函数和约束函数将其输入变量 x0 设置为 ODE 求解器的 4-D 初始点。如果抛射物击中墙壁，ODE 求解器不会停止。相反，约束函数只是变成正值，表示初始值不可行。

初始位置 x0(1) 不能高于 0，低于-200 也是没有意义的。（它应该接近 -20，因为在没有空气阻力的情况下，最长弹道将从 -20 以 pi/4 的角度开始。）类似地，初始角度 x0(2) 不能低于 0，也不能高于 pi/2。将边界设置得稍微远离这些初始值：

lb = [-200;0.05];
ub = [-1;pi/2-.05];
x0 = [-30,pi/3]; % Initial guess

将 UseCompletePoll 选项设置为 true。这给出了更高质量的解，并能够与并行处理直接进行比较，因为并行计算需要这种设置。

opts = optimoptions('patternsearch','UseCompletePoll',true);

调用 patternsearch 以求解问题。

tic % Time the solution
[xsolution,distance,eflag,outpt] = patternsearch(@cannonobjective,x0,...
    [],[],[],[],lb,ub,@cannonconstraint,opts)
toc
Optimization terminated: mesh size less than options.MeshTolerance
 and constraint violation is less than options.ConstraintTolerance.

xsolution =

  -28.8123    0.6095


distance =

 -125.9880


eflag =

     1


outpt = 

  struct with fields:

         function: @cannonobjective
      problemtype: 'nonlinearconstr'
       pollmethod: 'gpspositivebasis2n'
    maxconstraint: 0
     searchmethod: []
       iterations: 5
        funccount: 269
         meshsize: 8.9125e-07
         rngstate: [1×1 struct]
          message: 'Optimization terminated: mesh size less than options.MeshTolerance↵ and constraint violation is less than options.ConstraintTolerance.'

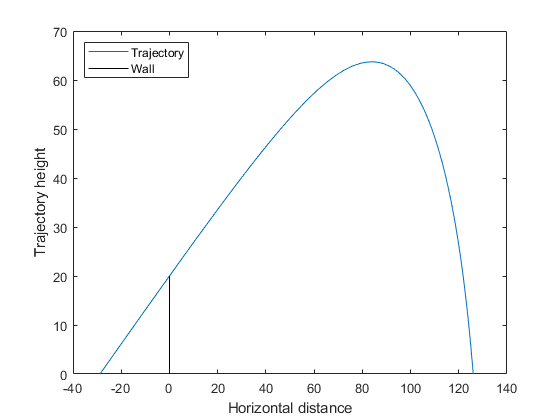
Elapsed time is 0.792152 seconds.

从距离墙壁约 29 米处以 0.6095 弧度的角度发射抛射物，最远距离约为 126 米。报告的距离为负数，因为目标函数是到墙壁的距离的负数。

将解可视化。

x0 = [xsolution(1);0;300*cos(xsolution(2));300*sin(xsolution(2))];

sol = ode45(@cannonfodder,[0,15],x0);
% Find the time when the projectile lands
zerofnd = fzero(@(r)deval(sol,r,2),[sol.x(2),sol.x(end)]);
t = linspace(0,zerofnd); % equal times for plot
xs = deval(sol,t,1); % Interpolated x values
ys = deval(sol,t,2); % Interpolated y values
plot(xs,ys)
hold on
plot([0,0],[0,20],'k') % Draw the wall
xlabel('Horizontal distance')
ylabel('Trajectory height')
legend('Trajectory','Wall','Location','NW')
ylim([0 70])
hold off

步骤 4.避免两次调用昂贵的子程序。

目标函数和非线性约束函数都调用 ODE 求解器来计算它们的值。使用同一函数中的目标和非线性约束中的技术来避免两次调用求解器。runcannon 文件实现了这项技术。将此文件复制到 MATLAB 路径上的文件夹中。

function [x,f,eflag,outpt] = runcannon(x0,opts)

if nargin == 1 % No options supplied
    opts = [];
end

xLast = []; % Last place ode solver was called
sol = []; % ODE solution structure

fun = @objfun; % The objective function, nested below
cfun = @constr; % The constraint function, nested below

lb = [-200;0.05];
ub = [-1;pi/2-.05];

% Call patternsearch
[x,f,eflag,outpt] = patternsearch(fun,x0,[],[],[],[],lb,ub,cfun,opts);

    function y = objfun(x)
        if ~isequal(x,xLast) % Check if computation is necessary
            x0 = [x(1);0;300*cos(x(2));300*sin(x(2))];
            sol = ode45(@cannonfodder,[0,15],x0);
            xLast = x;
        end
        % Now compute objective function
        % First find when the projectile hits the ground
        zerofnd = fzero(@(r)deval(sol,r,2),[sol.x(2),sol.x(end)]);
        % Then compute the x-position at that time
        y = deval(sol,zerofnd,1);
        y = -y; % take negative of distance
    end

    function [c,ceq] = constr(x)
       ceq = [];
        if ~isequal(x,xLast) % Check if computation is necessary
            x0 = [x(1);0;300*cos(x(2));300*sin(x(2))];
            sol = ode45(@cannonfodder,[0,15],x0);
            xLast = x;
        end
        % Now compute constraint functions
        % First find when the projectile crosses x = 0
        zerofnd = fzero(@(r)deval(sol,r,1),[sol.x(1),sol.x(end)]);
        % Then find the height there, and subtract from 20
        c = 20 - deval(sol,zerofnd,2);
    end

end

重新初始化问题并将调用时间设定为 runcannon。

x0 = [-30;pi/3];
tic
[xsolution,distance,eflag,outpt] = runcannon(x0,opts);
toc
Optimization terminated: mesh size less than options.MeshTolerance
 and constraint violation is less than options.ConstraintTolerance.
Elapsed time is 0.670715 seconds.

求解器运行速度比以前更快。如果您检查解，您会发现输出是相同的。

步骤 5.并行计算。

尝试通过并行计算来节省更多时间。首先开启一个并行工作进程池。

parpool
Starting parpool using the 'local' profile ...
Connected to the parallel pool (number of workers: 6).

ans = 

 ProcessPool with properties: 

            Connected: true
           NumWorkers: 6
              Cluster: local
        AttachedFiles: {}
    AutoAddClientPath: true
          IdleTimeout: 30 minutes (30 minutes remaining)
          SpmdEnabled: true

设置选项以使用并行计算，然后重新运行求解器。

opts = optimoptions('patternsearch',opts,'UseParallel',true);
x0 = [-30;pi/3];
tic
[xsolution,distance,eflag,outpt] = runcannon(x0,opts);
toc
Optimization terminated: mesh size less than options.MeshTolerance
 and constraint violation is less than options.ConstraintTolerance.
Elapsed time is 1.894515 seconds.

在这种情况下，并行计算速度较慢。如果您检查解，您会发现输出是相同的。

步骤 6.与遗传算法进行比较。

您还可以尝试使用遗传算法来解决该问题。然而，遗传算法通常速度较慢且可靠性较差。

正如同一函数中的目标和非线性约束中所述，使用 ga 时无法通过步骤 4 中 patternsearch 所使用的嵌套函数技术来节省时间。相反，通过设置适当的选项并行调用 ga。

options = optimoptions('ga','UseParallel',true);
rng default % For reproducibility
tic % Time the solution
[xsolution,distance,eflag,outpt] = ga(@cannonobjective,2,...
    [],[],[],[],lb,ub,@cannonconstraint,options)
toc
Optimization terminated: average change in the fitness value less than options.FunctionTolerance
 and constraint violation is less than options.ConstraintTolerance.

xsolution =

  -37.6217    0.4926


distance =

 -122.2181


eflag =

     1


outpt = 

  struct with fields:

      problemtype: 'nonlinearconstr'
         rngstate: [1×1 struct]
      generations: 4
        funccount: 9874
          message: 'Optimization terminated: average change in the fitness value less than options.FunctionTolerance↵ and constraint violation is less than options.ConstraintTolerance.'
    maxconstraint: 0
       hybridflag: []

Elapsed time is 12.529131 seconds.

ga 解不如 patternsearch 解：122 米对 126 米。ga 花费的时间更多：大约 12 秒对 2 秒以下；patternsearch 在串行和嵌套中花费的时间甚至更少，少于 1 秒。串行运行 ga 需要更长的时间，一次测试运行大约需要 30 秒。

另请参阅

主题