非线性约束的替代优化

此示例说明如何在替代优化中包含非线性不等式约束。该示例解决了具有非线性约束的 ODE。示例并行优化 ODE 展示了如何使用接受非线性约束的其他求解器来解决相同的问题。

有关此示例的视频概述，请参阅替代优化。

问题描述

问题是改变大炮的位置和角度，以便将炮弹发射到尽可能远的墙壁之外。该炮的炮口速度为 300 米/秒。墙高 20 米。如果大炮离墙壁太近，它射击的角度就会太陡，射弹的飞行距离就不够远。如果大炮离墙壁太远，射弹就飞得不够远。

非线性空气阻力会使射弹的速度减慢。阻力与速度的平方成正比，比例常数为 0.02。重力作用于抛射物，使其以恒定的 9.81 m/s^2 的速度向下加速。因此，轨迹 x(t) 的运动方程为

$\frac{d^{2} x (t)}{d t^{2}} = - 0.02 ‖ v (t) ‖ v (t) - (0, 9.81),$

其中 $v (t) = d x (t) / d t$ 。

初始位置 x0 和初始速度 xp0 是二维向量。但是初始高度 x0(2) 为 0，因此初始位置由标量 x0(1) 给出。初速度为 300（枪口速度），因此仅取决于初始角度，而初始角度是一个标量。对于初始角度 th，初始速度为 xp0 = 300*(cos(th),sin(th))。因此，优化问题仅取决于两个标量，使其成为二维问题。使用水平距离和初始角度作为决策变量。

构建 ODE 模型

ODE 求解器要求您将模型制定为一阶系统。用轨迹向量 $(x_{1} (t), x_{2} (t))$ 的时间导数 $(x_{1}' (t), x_{2}' (t))$ 来增强该轨迹向量，以形成四维轨迹向量。就这个增广向量而言，微分方程变成

$\frac{d}{dt} x (t) = [\begin{array}{c} x_{3} (t) \\ x_{4} (t) \\ - 0.02 ‖ (x_{3} (t), x_{4} (t)) ‖ x_{3} (t) \\ - 0.02 ‖ (x_{3} (t), x_{4} (t)) ‖ x_{4} (t) - 9.81 \end{array}] .$

cannonshot 文件实现了这个微分方程。

type cannonshot

function f = cannonshot(~,x)

f = [x(3);x(4);x(3);x(4)]; % initial, gets f(1) and f(2) correct
nrm = norm(x(3:4)) * .02; % norm of the velocity times constant
f(3) = -x(3)*nrm; % horizontal acceleration
f(4) = -x(4)*nrm - 9.81; % vertical acceleration

可视化该 ODE 的解，从距墙壁 30 米处开始，初始角度为 pi/3。plotcannonsolution 函数使用 ode45 来求解微分方程。

type plotcannonsolution

function dist = plotcannonsolution(x)
% Change initial 2-D point x to 4-D x0
x0 = [x(1);0;300*cos(x(2));300*sin(x(2))];
sol = ode45(@cannonshot,[0,15],x0);
% Find the time when the projectile lands
zerofnd = fzero(@(r)deval(sol,r,2),[sol.x(2),sol.x(end)]);
t = linspace(0,zerofnd); % equal times for plot
xs = deval(sol,t,1); % interpolated x values
ys = deval(sol,t,2); % interpolated y values
plot(xs,ys)
hold on
plot([0,0],[0,20],'k') % Draw the wall
xlabel('Horizontal distance')
ylabel('Trajectory height')
ylim([0 100])
legend('Trajectory','Wall','Location','NW')
dist = xs(end);
title(sprintf('Distance %f',dist))
hold off

plotcannonsolution 使用 fzero 来查找射弹落地的时间，即其高度为 0。射弹在 15 秒之前落地，因此 plotcannonsolution 使用 15 作为 ODE 解的时间量。

x0 = [-30;pi/3];
dist = plotcannonsolution(x0);

Figure contains an axes object. The axes object with title Distance 76.750599, xlabel Horizontal distance, ylabel Trajectory height contains 2 objects of type line. These objects represent Trajectory, Wall.

准备优化

为了优化初始位置和角度，编写一个类似于前面绘图例程的函数。从任意水平位置和初始角度开始计算轨迹。

包括合理的边界约束。水平位置不能大于 0。设置上界为 -1。同样，水平位置不能低于 -200，因此设置下界为 -200。初始角度必须为正数，因此将其下界设置为 0.05。初始角度不应超过 pi/2；将其上界设置为 pi/2 – 0.05。

lb = [-200;0.05];
ub = [-1;pi/2-.05];

编写一个目标函数，在给定初始位置和角度的情况下，返回与墙壁距离的负数。如果轨迹在小于 20 的高度处穿过墙壁，则轨迹不可行；此约束是非线性约束。cannonobjcon 函数实现目标函数计算。为了实现非线性约束，函数调用 fzero 来查找射弹的 x 值为零的时间。该函数通过检查时间 15 之后射弹的 x 值是否大于零来解释 fzero 函数失败的可能性。如果不是，那么该函数将跳过查找射弹穿过墙壁的时间的步骤。

type cannonobjcon

function f = cannonobjcon(x)
    % Change initial 2-D point x to 4-D x0
    x0 = [x(1);0;300*cos(x(2));300*sin(x(2))];
    % Solve for trajectory
    sol = ode45(@cannonshot,[0,15],x0);
    % Find time t when trajectory height = 0
    zerofnd = fzero(@(r)deval(sol,r,2),[1e-2,15]);
    % Find the horizontal position at that time
    dist = deval(sol,zerofnd,1);
    % What is the height when the projectile crosses the wall at x = 0?
    if deval(sol,15,1) > 0
        wallfnd = fzero(@(r)deval(sol,r,1),[0,15]);
        height = deval(sol,wallfnd,2);
    else
        height = deval(sol,15,2);
    end
    f.Ineq = 20 - height; % height must be above 20
    % Take negative of distance for maximization
    f.Fval = -dist;
end

您已经计算出一条可行的初始轨迹。使用该值作为初始点。

fx0 = cannonobjcon(x0);
fx0.X = x0;

使用 `surrogateopt` 解决优化问题

设置 surrogateopt 选项以使用初始点。为了实现可再现性，请将随机数生成器设置为 default。使用 'surrogateoptplot' 绘图函数。运行优化。要了解 'surrogateoptplot' 图，请参阅解释 surrogateoptplot。

opts = optimoptions('surrogateopt','InitialPoints',x0,'PlotFcn','surrogateoptplot');
rng default
[xsolution,distance,exitflag,output] = surrogateopt(@cannonobjcon,lb,ub,opts)

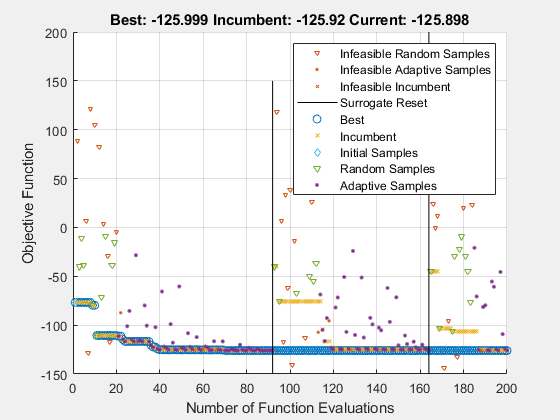
surrogateopt stopped because it exceeded the function evaluation limit set by 
'options.MaxFunctionEvaluations'.

xsolution = 1×2

  -28.4081    0.6160

distance = 
-125.9988

exitflag = 
0

output = struct with fields:
        elapsedtime: 47.0823
          funccount: 200
    constrviolation: 8.4347e-04
               ineq: 8.4347e-04
           rngstate: [1×1 struct]
            message: 'surrogateopt stopped because it exceeded the function evaluation limit set by ↵'options.MaxFunctionEvaluations'.'

绘制最终轨迹。

figure
dist = plotcannonsolution(xsolution);

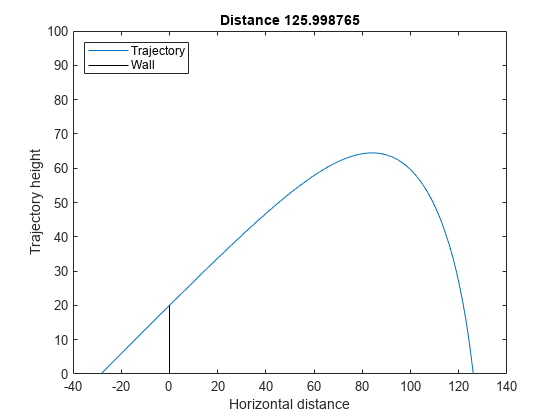
Figure contains an axes object. The axes object with title Distance 125.998765, xlabel Horizontal distance, ylabel Trajectory height contains 2 objects of type line. These objects represent Trajectory, Wall.

并行优化 ODE 中的 patternsearch 解显示最终距离为 125.9880，与这个 surrogateopt 解几乎相同。

另请参阅

surrogateopt