在广义模式搜索中使用完整轮询
假设有以下函数。
下图显示了该函数的图。
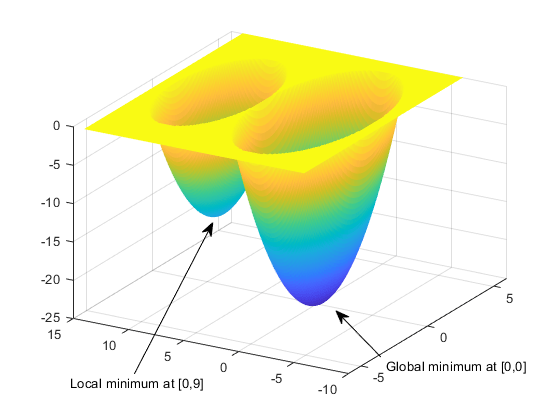
该函数的全局最小值出现在 (0, 0) 处,此处其值为 -25。然而,该函数在 (0, 9) 处也有一个局部最小值,其值为 -16。
要创建计算函数的文件,请将以下代码复制并粘贴到 MATLAB® 编辑器中的新文件中。
function z = poll_example(x) if x(1)^2 + x(2)^2 <= 25 z = x(1)^2 + x(2)^2 - 25; elseif x(1)^2 + (x(2) - 9)^2 <= 16 z = x(1)^2 + (x(2) - 9)^2 - 16; else z = 0; end end
将文件作为 poll_example.m 保存到 MATLAB 路径上的某个文件夹中。
要对函数运行模式搜索,请输入以下内容。
options = optimoptions('patternsearch','Display','iter'); [x,fval] = patternsearch(@poll_example,[0,5],... [],[],[],[],[],[],[],options)
MATLAB 返回迭代表和解方案。
x =
0 9
fval =
-16算法首先在初始点 f(0, 5) = 0. 处评估函数,轮询在其第一次迭代期间评估以下内容。
| f((0, 5)+ (1, 0)) = f(1, 5) = 0 | (1) |
| f((0, 5) + (0, 1)) = f(0, 6) = -7 | (2) |
一旦搜索轮询网格点 (0, 6),此时目标函数值小于初始点,它将停止轮询当前网格,并将下一次迭代的当前点设置为 (0, 6)。因此,在第一次迭代中,搜索向 (0, 9) 处的局部最小值移动。您可以通过查看命令行显示的前两行来看到这一点。
Iter f-count f(x) MeshSize Method
0 1 0 1
1 3 -7 2 Successful Poll请注意,模式搜索在第一次迭代中仅对目标函数执行两次评估,从而将总函数数从 1 增加到 3。
接下来,将 UseCompletePoll 设置为 true 并重新运行优化。
options.UseCompletePoll = true;
[x,fval] = patternsearch(@poll_example,[0,5],...
[],[],[],[],[],[],[],options);这一次,模式搜索在 (0, 0) 处找到全局最小值。本次运行与上一次运行的区别在于,将 UseCompletePoll 设置为 true,在第一次迭代中,模式搜索轮询所有四个网格点。
| f((0, 5) + (1, 0)) = f(1, 5) = 0 | (3) |
| f((0, 5)+ (0, 1)) = f(0, 6) = -6 | (4) |
| f((0, 5)+ (-1, 0)) = f(-1, 5) = 0 | (5) |
| f((0, 5) + (0, -1)) = f(0, 4) = -9 | (6) |
由于最后一个网格点具有最低的目标函数值,模式搜索选择它作为下一次迭代的当前点。命令行显示的前两行显示了这一点。
Iter f-count f(x) MeshSize Method
0 1 0 1
1 5 -9 2 Successful Poll在这种情况下,目标函数在第一次迭代时被评估四次。因此,模式搜索向 (0, 0) 处的全局最小值移动。
下图比较了 Complete 轮询设置为 Off 时返回的点序列与 Complete 轮询为 On 时返回的点序列。

